Краткие теоретические сведения
Теория вероятностей как математическая основа теории надежно-
Сти
Как известно, теория надежности технических систем (ТС), в первую
очередь, изучает поведение системы с точки зрения возможности появления
внезапных или постепенных отказов. Отмеченные отказы представляют собой
случайные события, что обуславливает широкое использование в данной об-
ласти подходов и результатов теории вероятностей.
На практике инженерные расчеты надежности ТС предполагают вы-
полнение операций над случайными событиями, вычисление их вероятностей
применительно к различным ситуациям. Приведем ряд соотношений, выте-
кающих из теории вероятностей и применяемых при расчетах надежности
ТС.
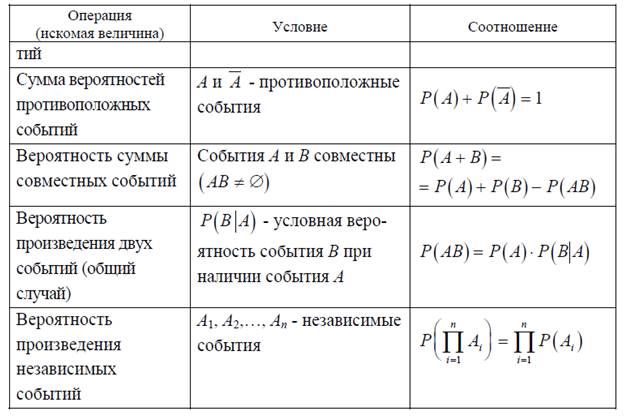
Вероятности композиций случайных событий
Правила выполнения операций, которым соответствуют вероятности
результирующих событий, представлены в таблице 1.1.
Таблица 1.1

Случайные величины и их характеристики
Одним из важнейших понятий теории вероятностей является понятие
случайной величины (СВ). Закон (функция) распределения F для случайной
величины X представляет вероятность P того, что она примет значение,
меньшее некоторой заданной величины x:

При этом различают два типа СВ: непрерывные и дискретные. Плотность распределения непрерывной СВ X в точке x определяется выражением:

График плотности распределения f (x) называют кривой распределе-
ния.
Вероятность попадания СВ в интервал от α до β и функцию F (x) ее
распределения при известной функции f (x) можно найти как


Отметим основные свойства плотности распределения:

Для описания свойств дискретной случайной величины обычно исполь-
зуется так называемый ряд распределения, который может быть представлен в
виде таблицы значений вероятностей pi того, что СВ X примет значения xi,
i = 1, n:

Числовые характеристики случайных величин
Во многих задачах определении показателей надежности ТС требуется
найти отдельные числовые характеристики, указывающие на существенные
черты распределения (например, математическое ожидание, дисперсию и
т.д.). Такие числовые характеристики и расчетные формулы для их нахожде-
ния представлены в таблице 1.2.
Таблица 1.2


Наиболее применимые в теории надежности законы распределения случайных величин
Наиболее употребительными при решении задач оценивания надежности ТС являются экспоненциальный и нормальный законы распределения. При этом в качестве случайной величины чаще всего фигурирует наработка T системы до отказа, которая соответствует функции распределения F (t). В некоторых ситуациях целесообразно оперировать функцией надежности, характеризующей вероятность противоположного отказу события:

Функции и плотности распределения для вышеназванных законов рас-
пределения СВ представлены в таблице 1.3.
Таблица 1.3

Для практических расчетов в случае нормального закона распределения применяют функцию Лапласа.

При этом производится переход от случайной величины T к величине,
имеющей нулевое математическое ожидание и единичную дисперсию:

Для значений функции Φ(z) составлены таблицы; она также является
встроенной функцией многих программных пакетов.
Задача 1. Имеются 4 ящика: 1) в первом - 2 белых и 3 черных шара; 2) во втором - 3 белых и 1 черный шар; 3) в третьем - 3 белых и 3 черных; 4) в четвертом - 2 белых и 2 черных. Из каждого ящика наугад вынимают по шару. Найти вероятность того, что все они будут одного цвета.
| № ящика | Вероятность (из соответствующего ящика) | |||||||
| P(A1)=2/5 | P(A2)=3/4 | P(A3)=3/6 | P(A4)=2/4 | |||||
| белые | 0,4 | 0,75 | 0,5 | 0,5 | ||||
| чёрные | P(B1)=3/5 | P(B2)=1/4 | P(B3)=3/6 | P(B4)=2/4 | ||||
| сумма | 0,6 | 0,25 | 0,5 | 0,5 | ||||
| А - из ящика взяли белый шар | Полная вероятность (из всех ящиков) | |||||||
| В - из ящика взяли чёрный шар | P(A)=P(A1*A2*A3*A4) | белые | ||||||
| С - из всех ящиков взяли шары одинакового цвета | 0,075 | |||||||
| P(B)=P(B1*B2*B3*B4) | чёрные | |||||||
| 0,0375 | ||||||||
| P(C)=P(A+B)=P(A)+P(B) | одного цвета | |||||||
| 0,1125 | ||||||||
| Ответ: | Вероятность того, что из всех ящиков вытянут шары одного цвета P(С) = 0,1125. |
Задача 2. Прибор состоит из 3-х блоков, причем 1-й может отказать с вероятностью 0.01, второй - с вероятностью 0.001, третий - с вероятностью 0.002. Перед вводом в эксплуатацию прибор проходит 2 вида испытаний.
При первом виде испытаний дефект 1-ого блока будет выявлен с вероятностью 0.7; второго - с вероятностью 0.5; третьего с вероятностью 0.4.
При втором виде испытаний дефект 1-го блока будет выявлен с вероятностью 0.9; второго - с вероятностью 0,2; третьего - с вероятностью 0.6. Прибор считается исправным, если исправны все три блока.
Найти: 1) вероятность того, что неисправный прибор будет выпущен в
эксплуатацию; 2) вероятность отказа прибора.
| № блока прибора | |||||||||||||
| Вероятность выпуска в эксплуатацию неисправного прибора, P(AB) | |||||||||||||
| Вероятность отказа | 0,01 | 0,001 | 0,002 | P(A)=q1*(1-P(А1))+q2*(1-P(А2))+q3*(1-P(А3)) | P(A)= | 0,0047 | |||||||
| P(В)=q1*(1-P(В1))+q2*(1-P(В2))+q3*(1-P(В3)) | P(B)= | 0,0026 | |||||||||||
| Вероятность выявления дефекта | P(AB)=P(A)*P(B) | 0,00001222 | |||||||||||
| При 1-ом испытании | 0,7 | 0,5 | 0,4 | Вероятность отказа прибора, Q | |||||||||
| Q = 1-P=1-(1-q1)*(1-q2)*(1-q3) = | 0,012968 | ||||||||||||
| При 2-ом испытании | 0,9 | 0,2 | 0,6 | ||||||||||
| Прибор исправен при исправности всех блоков | Ответ: | ||||||||||||
| A1 - 1й блок отказал, отказ не выявлен | 1) Вероятность того, что неисправный прибор будет выпущен в работу P(AB) = 0,00001222; | ||||||||||||
| A2 - 2й блок отказал, отказ не выявлен | |||||||||||||
| A3 - 3й блок отказал, отказ не выявлен | 2) Вероятность отказа приблра Q = 0,01296802. | ||||||||||||
| B1 - 1й блок отказал, отказ не выявлен | |||||||||||||
| B2 - 2й блок отказал, отказ не выявлен | |||||||||||||
| B3 - 3й блок отказал, отказ не выявлен | |||||||||||||
| q1 - вероятность отказа 1-го блока | |||||||||||||
| q2 - вероятность отказа 2-го блока | |||||||||||||
| q3 - вероятность отказа 3-го блока | |||||||||||||

| x | p | xi*pi | pi*(xi-mx)^2 | Мат. Ожидание |
| 0,2 | 0,001 | 0,0002 | 0,000040 | Mx=∑(xi*pi) |
| 0,3 | 0,002 | 0,0006 | 0,000180 | 0,7176 |
| 0,4 | 0,007 | 0,0028 | 0,001120 | Дисперсия |
| 0,5 | 0,12 | 0,06 | 0,030000 | Dx=∑(pi*(xi-mx)^2) |
| 0,6 | 0,4 | 0,24 | 0,144000 | 0,567140 |
| 0,7 | 0,22 | 0,154 | 0,107800 | |
| 0,8 | 0,1 | 0,08 | 0,064000 | |
| 0,05 | 0,05 | 0,050000 | ||
| 1,2 | 0,04 | 0,048 | 0,057600 | |
| 1,3 | 0,03 | 0,039 | 0,050700 | |
| 1,4 | 0,02 | 0,028 | 0,039200 | |
| 1,5 | 0,01 | 0,015 | 0,022500 | |
| Ответ: | 1) математическое ожидание mx = 0,7176; | |||
| 2) дисперсия Dx = 0,567. |
Задача 4. Значение сопротивления резистора имеет номинал 1 кОм, по-
грешность задания этой величины составляет 0,1 % и подчиняется нормаль-
ному закону распределения.
Найти вероятность того, что значение сопротивления будет лежать в
интервале от 999,5 Ом до 999,8 Ом.
Задача 5. Прибор состоит из основного блока и такого же резервного.
Для каждого из них вероятность безотказной работы подчиняется экспоненциальному закону:  . Оба блока работают 50 часов. Прибор отказывает при отказе обоих блоков.
. Оба блока работают 50 часов. Прибор отказывает при отказе обоих блоков.
Найти вероятность отказа прибора.