КОНТРОЛЬНАЯ РАБОТА ПО ИНФОРМАТИКЕ
ЦЕЛЬ РАБОТЫ
Закрепление знаний и практических навыков работы на персональном компьютере с использованием современных компьютерных технологий MS EXEL.
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
Контрольная работа состоит из 5 заданий, решение которых должно быть представлено в виде электронного варианта книги MS Excel и пояснительной записки, составленной в MS Word.
Задание 1. Табулировние и построение графиков функций.
Задание 2. Вычисление суммы функционального ряда.
Задание 3 Вычисление корней нелинейного (трансцендентного) уравнения, используя инструмент Подбор параметра.
Задание 4. Финансовый анализ в Excel на примерах использования: Подбор параметра и Диспетчера сценариев.
Задание 5. Применение возможностей Excel на примерах решения практических задач.
Задание 1
Тема: Табулирование и построение графиков функций
Постановка задачи. Построить графики двух функций Y=cos2x и Z=sin2x “по точкам” на отрезке -2π≤ X ≤2π c шагом  , где n-число разбиения отрезка.
, где n-число разбиения отрезка.
Решение
1. Строим математическую модель и определяем исходные и результирующие данные.
Исходные данные: начало и конец отрезка, число разбиений отрезка.
Результаты: столбец - аргумента X и два столбца функцийY и Z, которые вычисляются в каждой точке отрезка с шагом H. В нашем случае шаг вычисляется по формулеH=4π/n, где n=20.
2. Технология создания рабочего листа.
· Переименуем рабочий лист в “Табулирование”. Для этого дважды щелкнем мышкой по вкладке текущего рабочего листа и на вкладке листа введем имя “Табулирование”.
· Введем исходные данные с пояснениями и расчетные формулы для вычисления X,Y,Z,H в следующей последовательности:
Ø Ввод в ячейку F2 числа разбиений=20;
Ø Вычисление шага H: E2=4*ПИ()/$F$2;
Ø Формула вычисления начального значения X: B2=-2*ПИ();
Ø Удобно задавать описание X как функцию, в которой последующее значение X определяется через предыдущее,X=X+H.Тогда, сменив число разбиения n, автоматически произойдет пересчет по всем формулам на рабочем листе;
Ø Вычисление последующего значения X определяется по формуле B3=B2+$E$2;
Ø Формулы для вычисления начальных значений функций Y и Z определяются по формулам: C2=(cos(B2))^2; D2=sin(2*B2).
· Далее формулы X,Y, Z копируем вниз до последнего значения X.
Полученные результаты приведены на рабочем листе ”Табулирование” (рис.1), который представлен в режиме отображения значений. Внимательно посмотрите, правильно ли набраны формулы. Для этого представим рабочий лист в режиме отображения формул, который устанавливается нажатием клавиш Ctrl+ ` (` этот значок на клавише, расположенной в левом верхнем углу клавиатуры, где ~ (тильда)), или командой Сервис/Параметры/Вкладка Вид/Параметры окна-Формула. Проанализировав формулы, выполнив ту же последовательность команд, вернемся в режим отображений значений.
· Построение графиков по точкам.
Графики (диаграммы) можно создать с помощью команды Вставка/ Диаграмма или нажатием кнопки Мастер диаграмм на стандартной панели инструментов. Последовательность действий создания диаграммы:
Ø Выделите на рабочем листе данные, которые нужно отобразить- диапазон B1:D22;
Ø Нажмите на кнопку Мастер диаграмм;
Ø Выберите тип диаграммы – Точечный и нажмите на кнопку Далее;
Ø Выберите расположение данных- По строкам или По столбцам. Выберите По столбцам и нажмите на кнопку Далее;
Ø На соответствующих вкладках задайте параметры: заголовки и надписи данных и нажмите на кнопку Далее;
Ø Укажите, где должна находиться новая диаграмма, - На отдельном листе или уже Существующем. Выберите – На существующем листе и нажмите кнопку Готово.
На текущем рабочем листе появится Диаграмма-график. Как и любой объект, его можно выделить и перетащить с помощью мыши на новое место листа (рис.3).
Замечание.
Для построения одного графика Z=F(X) нужно Мастеру диаграмм задать несмежные области листа B2:B22 и D2:D22, которые можно выделить при нажатой клавише Ctrl.

Рис 1.

Рис.2

Рис. 3
Варианты заданий
| № | Уравнение y=f(x) | Уравнение z=f(x) | Отрезок, содержащий корень | Шаг |
 
| 
| [2; 3] | 0,1 | |

| 
| [0; 2] | 0,2 | |

| 
| [0,4; 1] | 0,05 | |

| 
| [0, 0,85] | 0,05 | |

| 
| [1; 2] | 0,1 | |

| 
| [0; 0,8] | 0,05 | |

| 
| [0; 1] | 0,1 | |

| 
| [2; 4] | 0,2 | |

| 
| [1; 2] | 0,1 | |

| 
| [0; 2] | 0,1 | |

| 
| [0.1; 1] | 0,1 | |

| 
| [1; 3] | 0,2 | |

| 
| [1,2; 2] | 0,08 | |
| ex+lnx-10x=н | 
| [3; 4] | 0,1 | |

| 
| [1; 2] | 0,1 | |
| 1-x+sinx-ln(1+x)=y | 
| [0; 1,5] | 0,15 | |
| 3x-14+ex-e-x=y | 
| [1; 3] | 0,2 | |

| 
| [0; 1] | 0,1 | |
| x+cos(x0,52+2)=y | 
| [0,5; 1] | 0,05 | |
| 3ln2x+6lnx-5=y | 
| [1; 3] | 0,2 | |
| sinx2+cosx2-10x=y | 
| [0; 1] | 0,1 | |
| x2 – ln(1+x) – 3=y | 
| [2; 3] | 0,1 | |
| 2x*sinx – cosx=y | 
| [0,4; 1] | 0,05 | |

| 
| [-1; 0] | 0,1 | |
| lnx – x + 1,8=y | 
| [2; 3] | 0,1 | |

| 
| [0,2; 1] | 0,05 | |

| 
| [1; 2] | 0,1 | |

| 
| [1; 2] | 0,1 | |

| 
| [0; 1] | 0,1 | |
| 0,6*3x-2,3*x – 3=y | 
| [2; 3] | 0,1 |
Задание 3
Нахождение корней нелинейных (трансцендентных) уравнений, используя инструмент «Подбор параметра»
Пример. Найти корни уравнения 
Из рис.1 видно, что функция меняет знак между значениями X диапазона [3,2;3,3]. Значит, в этом диапазоне существует корень. В качестве начального приближения Xкорень берем ячейку F3=3, значение функции Y задаем в ячейке F4=3*F3-4*ln(F3)-5.
Теперь выберем команду Сервис, Подбор параметра и заполним диалоговое окно Подбор параметра. Заполнение окна смотрите на рис.1.
После нажатия кнопки OK средство Подбора параметров находит приближенное значение корня, которое помещает в ячейку F3, а корень-результат в ячейку F4(смотрите рис.2).
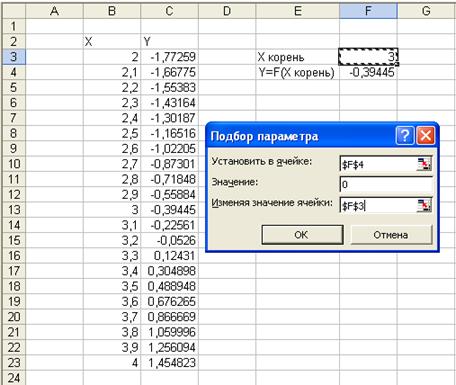
Рис.1

Рис.2
Варианты к заданию 3
| № | Уравнения | Отрезок, содержащий корень | Приближенное значение |
| 1-x+sinx-ln(1+x)=0 | [0; 1,5] | 1,1474 | |
| 3x-14+ex-e-x=0 | [1; 3] | 2,0692 | |

| [0; 1] | 0,5768 | |
| x+cos(x0,52+2)=0 | [0,5; 1] | 0,9892 | |
| 3ln2x+6lnx-5=0 | [1; 3] | 1,8832 | |
| sinx2+cosx2-10x=0 | [0; 1] | 0,1010 | |
| x2 - ln(1+x) - 3=0 | [2; 3] | 2,0267 | |
| 2x*sinx - cosx=0 | [0,4; 1] | 0,6533 | |

| [-1; 0] | - 0,2877 | |
| lnx - x + 1,8=0 | [2; 3] | 2,8459 | |

| [0,2; 1] | 0,5472 | |

| [1; 2] | 1,0769 | |

| [1; 2] | 1,2388 | |

| [0; 1] | 0,4538 | |
| 0,6*3x-2,3*x - 3=0 | [2; 3] | 2,4200 | |

| [2; 3] | 2,2985 | |

| [0; 2] | 1,0001 | |

| [0,4; 1] | 0,7376 | |

| [0; 0,85] | 0,2624 | |

| [1; 2] | 1,1183 | |

| [0; 0,8] | 0,3333 | |

| [0; 1] | 0,5629 | |

| [2; 4] | 3,2300 | |

| [1; 2] | 1,8756 | |

| [0; 1] | 0,7672 | |

| [0; 1] | 0,8814 | |

| [1; 3] | 1,3749 | |

| [1,2; 2] | 1,3077 | |
| ex+lnx-10x=0 | [3; 4] | 3,5265 | |

| [1; 2] | 1,0804 |