Полная энергия механической системы
Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии взаимодействия этих тел друг с другом и с внешними телами:
Е = Ек + Еп.
Приращение механической энергии системы определяется работой всех неконсервативных сил (внешних и внутренних):
.
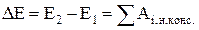Закон сохранения механической энергии: механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.
Закон сохранения и превращения энергии
Рассмотрим процесс изменения состояния тела, поднятого на высоту h. При этом его потенциальная энергия
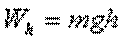
Тело начало свободно падать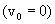 
. Из кинематики известно, что момент достижения поверхности земли оно будет иметь скорость 
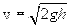икинетическую энергию:
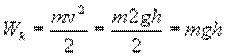
Кинетическая энергия тела, упавшего с высоты h, оказалась равной его потенциальной энергии, которую оно имело до начала падения. Следовательно:
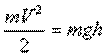
На поверхности Земли h=0 и потенциальная энергия 
, а 
-максимальна. В начале падения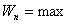 
, а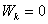 
т.е. потенциальная энергия переходит (превращается) в кинетическую. Таким образом, при падении тела в системе тело-Земля кинетическая энергия возрастает и, следовательно, ее изменение 
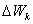равное работе 
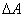, имеет положительный знак, т.е.
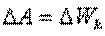
Потенциальная энергия - уменьшается, и, следовательно, ее изменение имеет знак минус. Поэтому можем записать:
Сложив две эти формулы, получим
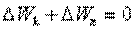
или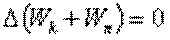 
Сумма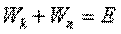 
представляет собой полную энергию, и, следовательно,
, а
|
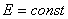
Таким образом, энергия замкнутой консервативной системы остается постоянной при всех, происходящих в ней процессах и превращениях. Энергия может переходить из одних видов в другие (механические, тепловые, и т.д.), но общее ее количество остается постоянным. Данное положение называют законом сохранения и превращения энергии.
Консервативная и диссипативные сисетмы
Консервативная система.
Простейший случай консервативной системы-это гамильтонова система, т.е. система, имеющая вид:
x'=dH/dy
y'=-dH/dx
где H(x,y)-аналитическая функция переменных x и y. Система, очевидно, имеет аналитический интеграл H(x,y)=C.
Консервативной системой мы будем называть систему
dx/dt=P(x,y), dy/dt=Q(x,y)
определенную в некоторой области плоскости G или на всей плоскости, которая после умножения правых частей на интегрирующий множитель M(x,y), являющийся аналитической функцией, не обращающейся в ноль во всей области вышеуказанной системы, и после изменения параметризации может быть приведена к гамильтонову виду
dx/dt1=M(x,y)*P(x,y)=dH/dy
dy/dt1=M(x,y)*Q(x,y)=-dH/dx
dt1=dt/M(x,y)
Диссипативная система
Диссипативная система — это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне. Диссипативная система иногда называется ещё стационарной открытой системой или неравновесной открытой системой.
Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем — несохранение объёма в фазовом пространстве, то есть невыполнение Теоремы Лиувилля.
Простым примером такой системы являются ячейки Бенара. В качестве более сложных примеров называются лазеры, реакция Белоусова — Жаботинского и биологическая жизнь.
Термин «диссипативная структура» введен Ильёй Пригожиным.
Последние исследования в области «диссипативных структур» позволяют делать вывод о том, что процесс «самоорганизации» происходит гораздо быстрее при наличии в системе внешних и внутренних «шумов». Таким образом, шумовые эффекты приводят к ускорению процесса «самоорганизации».