ТЕХНИЧЕСКОЙ СИСТЕМЫ СВЯЗИ НА ПРИМЕРЕ DX-500

ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА НИКОЛАЯ II»

_____________________________________________________________

Кафедра «Автоматика, телемеханика и связь на железнодорожном транспорте»

 

А.П. Богачев

 

 

ИССЛЕДОВАНИЕ НАДЕЖНОСТИ И РИСКА НЕРЕЗЕРВИРОВАННОЙ

ТЕХНИЧЕСКОЙ СИСТЕМЫСВЯЗИ НА ПРИМЕРЕ DX-500

Учебно-методическое пособие

 

Москва – 2016

 

 

федеральное государственное бюджетное образовательное учреждение
высшего образования

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА НИКОЛАЯ II»

_____________________________________________________________

Кафедра «Автоматика, телемеханика и связь на железнодорожном транспорте»

 

А.П. Богачев

 

 

ИССЛЕДОВАНИЕ НАДЕЖНОСТИ И РИСКА НЕРЕЗЕРВИРОВАННОЙ

ТЕХНИЧЕСКОЙ СИСТЕМЫСВЯЗИ НА ПРИМЕРЕ DX-500

Учебно-методическое пособие для студентов специальности «Системы обеспечения движения поездов» специализации «Телекоммуникационные системы и сети на железнодорожном транспорте»

 

Москва - 2016

УДК 656.256

Б 73

Богачев А.П. Исследование надежности и риска нерезервированной системы связи на примере DX-500: Учебно-методическое пособие. – М.: МГУПС (МИИТ), 2016. - 38 с.

 

 

В учебно-методическом пособии приводятся основные теоретические сведения из курса «Основы теории надежности», касающиеся анализа надежности работы нерезервированных систем связи. В лабораторной работе анализ надежности системы оценивается с применением аппарата компьютерной алгебры Derive 6.2. Кроме того, для выполнения лабораторной работы приводятся различные варианты параметров системы связи.

Рецензент: к.т.н., доцент кафедры «Управление безопасностью в техносфере» МГУПС

(МИИТ) Грибков О.И.

 

 

© МГУПС (МИИТ), 2016

 

1. ОПИСАНИЕ DX-500

1.1. Общие сведения

Система связи железных дорог - одна из старейших и, вероятно, самая сложная ведомственная система связи. В последние годы началась активная модернизация сетей связи железнодорожного транспорта. Устанавливаются цифровые учрежденческо-производственные автоматические телефонные станции (УПАТС), прокладываются тысячи километров волоконно-оптических линий связи, внедряются новые технологии, благодаря которым открываются новые возможности по управлению пассажирскими и грузовыми перевозками.

Одна из самых популярных УПАТС на железных дорогах это - «МиниКом DX-500». Сотни станций «МиниКом DX-500» успешно эксплуатируются на Октябрьской, Калининградской, Московской, Горьковской, Северной, Северо-Кавказской, Куйбышевской, Свердловской, Дальневосточной, Сахалинской и Ямальской железных дорогах.

На рис. 1.1 представлена одна из моделей УПАТС «МиниКом DX-500».

Рис. 1.1. УПАТС «МиниКомDX-500»

Понимая высокую степень ответственности телекоммуникационной техники в производственном процессе, разработчики станции «МиниКом DX-500» особое внимание уделили вопросам надежности и отказоустойчивости.

1.2. Надежность УПАТС «МиниКом DX-500»

Надежность УПАТС «МиниКом DX-500» характеризуется:

1. Распределенным управлением

Использование собственных микропроцессоров со своей памятью в каждом модуле позволяет распределить управление по всей системе. Надежность больше не определяется зависимостью от централизованной, а потому оказывающей большое влияние, функции управления. При децентрализованном управлении неисправность одного модуля оказывает ограниченное влияние на всю систему. Каждый кластер «МиниКом DX-500» имеет собственный микропроцессор и цифровое коммутационное поле, обеспечивающее коммутацию разговоров в пределах одного кластера.

2. Дублированием систем

Ресурсы станции, влияющие на согласованную работу отдельных модулей, используются централизованно. Центральное коммутирующее устройство и система межмодульной синхронизации выполнены с использованием принципа 100-процентного резервирования.

3. Построением системы электропитания

Система «МиниКом DX-500» построена с применением полностью децентрализованной системы электропитания. К станции подается напряжение 48 В или 60 В от внешних первичных источников питания по двум независимым внешним вводам. Каждая плата получает питание по независимым шинам. Плата автоматически выбирает шину электропитания, переключаясь на другую при отказе одного из источников. Таким образом, станция не имеет внутренних централизованных блоков питания [3].

Структурная схема «МиниКом DX-500» представлена на рис. 1.2.

 

 

В состав структурной схемы входит:

ВВП – внешний ввод питания;

CPU – модуль центрального коммутационного поля (центр);

ADK– управляющий абонентский кластер;

PCM – кластер ИКМ-трактов и цифровых терминальных интерфейсов

32N – аналоговая портовая плата c субмодулями СЛ (соединительные линии).

Благодаря такому количеству зарезервированных элементов и большой надежности УПАТС, мы создали лабораторные работы на основе схем УПАТС «МиниКом DX-500».

В лабораторных работах рассматриваются две подключенные между собой станции с резервирующими элементами и без резервирующих элементов.

2. ПРОГРАММА КОМПЬЮТЕРНОЙ АЛГЕБРЫDerive 6

2.1. Общие сведения

Основные возможности пакета символьных вычислений Derive 6:

- упрощение выражений;

- дифференцирование и интегрирование функций одной или нескольких переменных;

- решение систем линейных уравнений;

- решение задач матричной алгебры;

- решение нелинейных уравнений;

- решение дифференциальных уравнений;

- разложение функций в ряд;

- вычисление пределов;

- вычисление сумм рядов;

- построение графиков функций.

Система Derive 6 обладает следующими особенностями: проста в изучении; поддерживает интерактивный режим общения (запрос-ответ) пользователя с персональным компьютером (ПК), не предъявляет высоких требований к типу и техническим характеристикам компьютера (реализуется практически на любом современном ПК), обладает элементами интеллектуальной системы, при решении задач символьной математики, обеспечивает высокую производительность, устойчива к ошибкам вычислительного процесса, высокую достоверность решения задач.

Диалог с пользователем Derive 6 реализует по следующей схеме:

1. Ввод выражения.

2. Команда действий.

3. Ответ.

Такая схема решения математических задач обеспечивает пользователю максимум удобств и делает процесс решения задачи легким. Иногда, в сложных случаях, приходится набирать на клавиатуре и вводить в память компьютера команды. Но даже в этих случаях пользователь испытывает максимум удобств, благодаря автоматизации этих действий (например, подстановка данных в математические выражения, установка опций, ввод начальных значений и начальных условий и др.).

2.2. Визуальный интерфейс программы Derive 6

Главное окно системы Derive 6 показано на рис. 2.1.

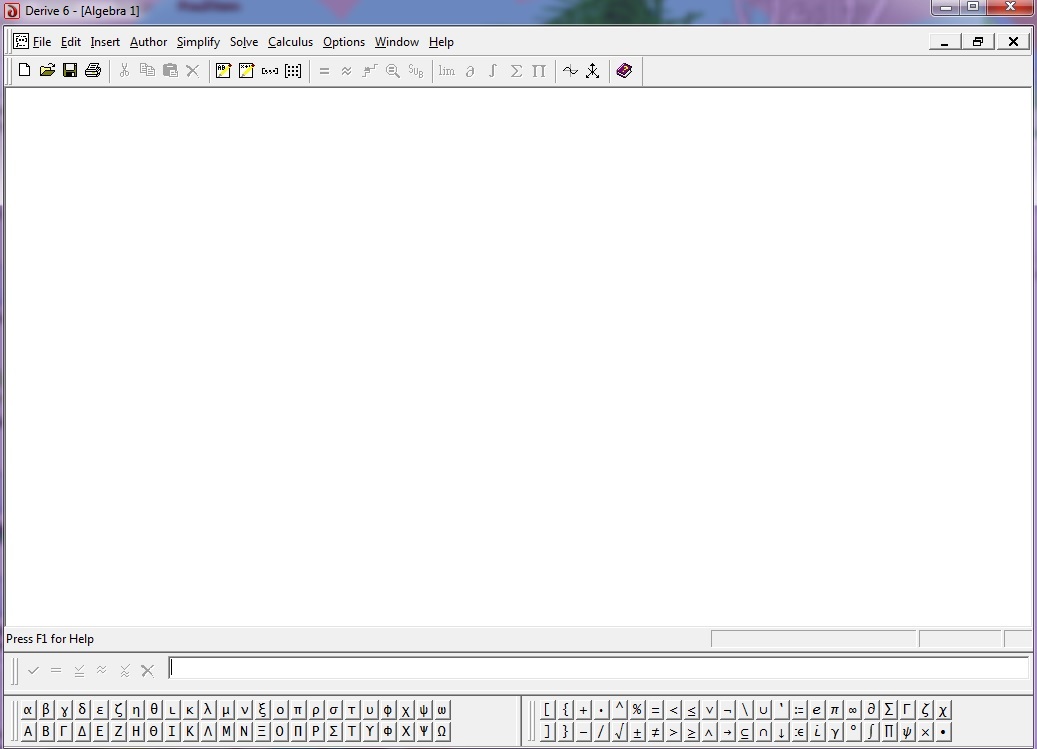
Рис. 2.1. Главное окно системы

Оно состоит из нескольких уникальных строк, каждая из которых имеет свое особое назначение. Рассмотрим назначение каждой из них в отдельности.

 

2.3. Назначение пунктов меню

Первая строка — строка заголовка и управления окном.

Она расположена в верхней части главного окна и в ней находится название системы — Derive 6, а также кнопки управления окном (свертывания, развертывания и закрытия).

Ниже строки заголовка расположена строка главного меню, рисунок 2.2.

Рис. 2.2. Строка главного меню

Эта строка содержит следующие пункты:

«File» -работа с файлами и принтером;

«Edit» - редактирование выражений;

«Insert» - открытие графических окон, аннотация к графикам;

«Author» - ввод математических выражений и текстов для их дальнейшего использования;

«Simplify» - преобразование и вычисление математических выражений;

«Solve» - решение уравнений и систем уравнений;

«Calculus» - вычисление производных, интегралов, пределов, сумм, произведений, разложение в ряд Тейлора;

«Options» - задание необходимых настроек системы Derive 6;

«Window» - открытие окон и работа с ними;

«Help» - включение справочной системы.

Активизация пунктов главного меню осуществляется по щелчку левой кнопки мыши с предварительной установкой ее указателя в область выбранной позиции меню. Возможен вариант использования "горячих" клавиш. В этом случае используется сочетание клавиши <Alt> и клавиши, помеченной буквой, которая соответствует подчеркнутой букве в названии команды. Эти способы применяются и для управления разными командами, для которых "горячие" клавиши указываются после имени команды.

Главное меню изменяется в зависимости от состояния системы. Так, например, если в системе закрыты все окна, то главное меню будет иметь только пункты «File», «Window» и «Help». Графическое окно имеет свое меню. В ряде случаев некоторые пункты главного меню недоступны пользователю (надписи в них сделаны затененным шрифтом) или вовсе отсутствуют.

Следующая строка - панель инструментов, рис. 2.3.

Рис. 2.3. Панель инструментов

Панель инструментов расположена в третьей сверху экранной строке. Она содержит кнопки быстрого управления системой, дублирующие команды главного меню. Каждая из кнопок вводит из множества команд главного меню лишь одну. Набор кнопок зависит от вида окна, открытого в данный момент.

Панель инструментов дублирует многие важные и часто используемые команды. При наличии этой панели (по желанию ее можно убрать с экрана) во многих случаях можно не обращаться к пунктам и командам главного меню, используя одноименные кнопки панели инструментов. Наиболее часто приходится пользоваться кнопками быстрого управления при работе с математическими выражениями.

Ниже приводятся названия кнопок, классифицированных по группам:

Команды работы с файлами:

«New» - открытие нового окна;

«Open» - вывод окна загрузки файла;

«Save» - сохранение данных в файле под текущим именем;

«Print» - печать содержимого окна.

Команды редактирования:

«Cut» - удаление выделенного выражения (множества выделенных выражений);

«Сору» - создание копии;

«Paste» - восстановление последнего удаленного выражения;

«Delete Object» - удаление выделенного выражения без его восстановления.

Команды ввода:

«Insert Text» - создание аннотаций;

«Author Expression» - ввод математических выражений;

«Author Vector» - задание вектора необходимой размерности;

«Author Matrix» - задание матрицы необходимой размерности.

Команды вычислений:

«Simplify» - символьные и точные вычисления в цифровой форме, упрощение математических выражений;

«Approximate» - вычисления в цифровом виде с представлением чисел в естественной форме;

«Solve Expression» - решение уравнений и систем уравнений;

«Variable Substitution» - подстановка значений переменных.

Команды специальных вычислений:

«Find limit» - вычисление пределов функций;

«Find Derivative» - вычисление производных;

«Find Integral» - вычисление интегралов;

«Find Sum» - вычисление сумм рядов;

«Find Product» - вычисление произведений рядов.

Команды графических окон:

«2D-plot window» - вывод окна двумерной графики;

«3D-plot window» - вывод окна трехмерной графики;

«Help About Derive» - информация о системе Derive.

За рассмотренными тремя экранными строками располагается окно выражений. Оно занимает большую часть экрана и размещается сразу за панелью инструментов. В этом окне находятся функции, математические выражения и другая информация. Строки в "окне выражений" нумеруются, благодаря чему имеется возможность выполнять математические действия над выражениями посредством номеров строк, в которых они находятся. Выделение строки осуществляется щелчком кнопки мыши в ее области. Над выделенными выражениями осуществляются действия путем команд главного меню или панели инструментов.

Следующим атрибутом интерфейса системы является диалоговое окно ввода выражений.

Диалоговое окно активизируется (мигающий курсор в окне) командой «Author Expression», или нажатием клавиши <F2>, или щелчком левой кнопки мыши в область диалогового окна. Это окно служит для ввода математических выражений и текстов.

Редактирование выражения, уже введенного и отображаемого в основном окне, осуществляется только путем его вызова в диалоговое окно, с последующим вводом как нового.

К диалоговому окну добавлена панель с математическими символами и символами латинского и греческого алфавитов, представленных на рис. 2.3.

Рис. 2.3. Панель с математическими символами и символами латинского и греческого алфавитов

Для ввода любого из символов достаточно указать на него курсором и щелкнуть левой кнопкой мыши. При этом курсор диалогового окна следует установить в месте ввода символа.

Слева от диалогового окна расположены пять кнопок. Они позволяют получать решения в различном виде без предварительного ввода вычисляемого выражения. Кнопки имеют следующие имена и назначения:

«Author Expression» - ввод выражения (кнопка, дублирующая клавишу <Enter>);

«Simplify» - упрощение вводимого выражения или его вычисление;

«Author and Approximate» - ввод и вычисление выражения (на экране появляется выражение и его вычисленное значение).

Арифметическими операторами системы Derive 6 являются:

+ - сложение (например, (а + b));

- - вычитание (например, (a-b));

* - умножение (например, (а * b));

/ - деление ();

^ - возведение в степень (a^b);

% - вычисление процентов.

Операция умножения при вводе математических выражений мо­жет быть реализована несколькими способами. При умножении двух чисел или двух символьных переменных необходимо при­менить знак умножения (*) или нажать клавишу <Пробел>. Если же умножается число на символьную переменную, то знак умно­жения или <Пробел> можно не применять. При любом способе ввода знака умножения на экране символ умножения обозначает­ся точкой.

При возведении числа или символьной переменной в отрица­тельную степень скобки можно не использовать. Вместо очевид­ной записи а^{^}(-2) можно вводить а^{^} - 2. Здесь допускаются два арифметических оператора подряд.

Ввод математических выражений осуществляется в латинском алфавите.

Последовательность команд при вводе выражений:

1. «Autor Expression» (или <Ctrl> + <A>).

2. Запись выражения в диалоговом окне.

3. Нажатие клавиши <Enter> или щелчок мыши по кнопке V (слева от диалогового окна).

На экране появляется выражение с символом #1:, что означает номер строки, в которой оно находится. При вводе выражений можно пользоваться панелями математических символов, приве­денных в двух нижних строках экрана. Пример записи представлен на рис. 2.4.

 

Рис. 2.4. Пример записи выражения

3. ПОРЯДОКВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

 

Для выполнения лабораторной работы «Исследование надежности и риска нерезервированной технической системы» использована схема подключения 2-х «МиниКом DX-500» друг с другом посредством оптического канала без резервирования. На рис. 3.1 представлена структурная схема подключения.

 

Рис. 3.1. Структурная схема подключения 2-х «DX-500»

 

В состав структурной схемы входит:

ВВП - внешний ввод питания;

CPU- модуль центрального коммутационного поля (центр);

PCM - кластер ИКМ- трактов и цифровых терминальных интерфейсов;

модем; оптоволокно.

В данной лабораторной работе мы будем использовать конфигурацию DX-500 без резервного модуля центрального коммутационного поля (CPU) и без резервного внешнего питания (ВВП), чтобы исследовать надежность и риски нерезервированной технической системы.

 

3.1. Постановка задачи

Дано:

Структурная схема системы в виде основного (последовательного в смысле надежности) соединения элементов;

n — число элементов системы;

λ_i — интенсивность отказа i- го элемента системы, i =1, 2, …, n;

r_i — риск из –за отказа i- го элемента системы, i= 1, 2, …, n;

R— допустимый риск;

T— суммарное время работы системы.

Определить:

Показатели надежности системы:

P_c(t)— вероятность безотказной работы системы в течении времени t, а также ее значения при t=T и t=T₁;

T₁ — среднее время безотказной работы системы;

R_c(t) — риск системы как функцию времени; значение риска при t=T и t=T₁;

Возможность расчета риска по приближенной формуле.

 

3.2. Сведения из теории

Основными показателями надежности нерезервированной невосстанавливаемой системы являются: P_c(t) — вероятность безотказной работы системы в течение времени t, T₁ — среднее время безотказной работы. При постоянных интенсивностях отказов элементов

, ,

где — интенсивность отказа системы.

Риск системы R_c(t) и R_c^*(t) вычисляется по следующим формулам:

, (3.1)

, (3.2)

где Q_c(t) = 1-P_c(t) - вероятность отказа системы в течение времени t; q_i(t) - вероятность отказа i -го элемента системы в течение времени t.

Формула (3.1) является точной, формула (3.2) - приближенной. Если элементы системы одинаково надёжны, то отношение R_c(t) к R_c^*(t) имеет вид:

. (3.3)

G_R(t,n) является убывающей функцией времени, при этом:

,

Это означает, что с увеличением длительности времени работы системы погрешность приближенной формулы увеличивается.

3.3. Последовательность выполнения работы

Лабораторную работу следует выполнять в такой последовательности:

1. Вычислить показатели надежности системы P_c(t) и T_i. Значение вероятности безотказной работы P_c(t) следует получить при t=T и t=T₁.

2. Исследовать функцию риска системы по точной формуле (3.1), для чего:

Получить формулу риска для заданных n, λ_i, r_i.

Исследовать зависимость R_c(t), представив функцию в виде графика и таблицы;

Вычислить значение риска для исходных данных своего варианта при t=T и t=T₁.

3. Исследовать зависимость G_R(t,n) при допущении, что элементы системы равно надежны и интенсивность отказа каждого элемента равна их средней интенсивности отказов, т.е. .

4. Сделать выводы.

 

 

По результатам лабораторной работы представляется отчет, в котором обязательными являются следующие пункты:

1. Постановка задачи.

2. Расчетные формулы.

3. Численные значения показателей надежности и риска исследуемой системы.

4. Значение времени непрерывной работы системы, при котором обеспечивается требуемое значение риска.

5. Графики и таблицы функций риска.

6. Выводы по результатам исследований.

3.4. Пример выполнения лабораторной работы

Пусть дана система со следующими исходными данными:

число элементов системы n= 9;

время непрерывной работы T =1000 ч;

допустимый риск R =5000 у.е.

Значение риска и интенсивностей отказов элементов приведены в таблице3.1. Для того, чтобы создать несколько вариантов численных значений для выполнения лабораторных работ будем считать, что станции работают в разных условиях, следовательно, имеют разные интенсивности отказов и риски из-за отказов.

Далее приводится последовательность выполнения работы. Исследования будем проводить с помощью универсальной системы символьной математики Derive 6.

Таблица 3.1

Исходные данные примера

Номера элементов
λ·10-5, ч.-1	1,2	0,8	0,5		1,5	0,6	0,09	0,05
r, у.е.

3.5. Определение показателей надежности системы

Интенсивность отказов системы равна . Подставляя в это выражение значения интенсивности отказов элементов из табл. 3.1, получим: λ_c=8,24·10^-5 ч.^-1 (технология вычисления λ_c с помощью системы Derive 6 приведена далее.

Тогда вероятность и среднее время безотказной работы будут равны:

, ч.

При t=T =1000 ч. P_c (1000)= .

3.6. Определение риска системы по точной формуле

Для образования вектора интенсивностей отказов и вектора риска r в системе Derive 6 необходимо выполнить следующие действия:

1. Выбрать пункт меню «Author → Vector», на экране появится окно «Vector Setup »;

2. Ввести размер вектора (в нашем случае 9), нажать кнопку OK, на экране монитора появится окно ввода элементов вектора «Auhor 10 element vector»;

3. Ввести интенсивности отказов элементов (для ускорения процедуры ввода значения λ не умножается на 10^-5), после нажатия кнопки OK на экране в строке #1 отобразится вектор интенсивностей отказов элементов.

Аналогично образуется вектор риска r. Пусть он находится в строке #2.

Вычисление интенсивности отказов системы λ_с осуществляется с помощью следующих действий:

Набрать в строке пользователя функцию: ELEMENT (#1, n), после нажатия клавиши <Enter> на экране появится функция ELEMENT с вектором интенсивностей отказов.

Внимание.

В функции ELEMENT первым аргументом должен быть номер строки с вектором λ, определенным ранее, а вторым аргументом - символ n, а не его численное значение.

Щелкнуть на кнопке «Find Sum» панели инструментов, на экране появится новое окно «Calculus Sum». На вкладке «Variable» установить значение n, на вкладке «Sum» установить переключатель в положение «Definite», на вкладке «Definite Sum» определить область суммирования (в нашем случае от 1 (Lower Limit) до 9 (Upper Limit)). После нажатия ОК на экране монитора отобразится выражение суммы элементов вектора λ_с.

Нажать кнопку «Approximate» панели инструментов, на экране монитора появится искомое значение суммы интенсивностей отказов элементов. В нашем случае с учетом масштаба (10^-5) λ_с =8,24·10^-5ч.^-1

Для вычисления суммы 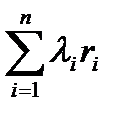необходимо получить скалярное произведение векторов λ и r, которые в нашем примере находятся соответственно под номерами #1 и #2. Для этого в строке пользователя набираются выражения #1и #2, далее нажимаются клавиша < Enter > и кнопка «Approximate» панели инструментов, на экране монитора появляется ответ 1,0506·10⁴. В нашем случае с учетом масштаба интенсивностей отказа (10^-5) искомая сумма равна 0,10506.

Процедуры решения (рис. 3.2) на экране монитора имеют следующий вид:

Рис. 3.2. Вычисление интенсивности отказов системы λ_с

Так как Q_c(t)=1-P_c(t)=1-e^-λ_c^t, λ_c= 8,24·10^-5, то в соответствии с (3.1) функция будет равна:

или

.

Вычисление R_c(t) для заданного значения времени непрерывной работы t=T и среднего времени безотказной работы t=T₁ выполняется с помощью кнопок «Variable Substitute» и «Approximate» панели инструментов. Для нашего примера при t = 1000 ч. риск R_c (1000)=100,848.

Для t=T₁ =12136 ч. значение риска R_c(t) = 805,953. Из полученных значений R_c(t) видно, что риск исследуемой системы ниже допустимого значения, равного 5000 условных единиц.

3.7. Исследование функции риска

Предполагая, что все элементы системы равно надежны, а интенсивность отказа каждого элемента ч.^-1, получим следующее выражение риска:

Найдем зависимость R_c(t) при различных значениях n в виде графиков и таблиц, используя возможности пакета Derive 6.

 

3.8. Получение графика функции риска

Построим графики функции риска, выполнив следующие действия:

1. Ввести выражение риска R_c(t,n) = .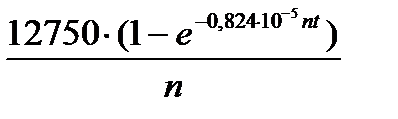

2. Получить выражение риска для различных значений n путем подстановки в выражение риска численных значений n с помощью кнопки «Sub» панели инструментов, на экране появится выражения риска (в нашем случае при n =10, 30,50);

3. Щелкнуть мышью на кнопке «2D-plot window» панели инструментов, на экране появится окно «2D-plot» с сеткой координат;

4. настроить с помощью клавиш <F5> — <F10> оси координат на нужный диапазон времени (ось x) и риска (ось y);

5. после нажатия кнопки «Plot Expression» панели инструментов на экране появится график функции риска при данном n;

6. щелкнуть мышью на кнопке «Algebra window» панели инструментов графического окна, на экране появится главное окно системы;

7. выделить формулу риска при новом значении n (в нашем случае при n = 30) и построить график описанным ранее способом и т.д. На экране образуется семейство графиков (в нашем случае три графика при n =10, 30, 50).

Далее приводятся процедуры образования функций риска (рис. 3.3) и соответствующих им графиков (рис. 3.4).

Рис. 3.3. Процедура образования функции риска

Из рис. 3.4 видно, что с увеличением времени t работы системы техногенный риск функционирования системы увеличивается и при t стремится к постоянной величине, равной среднему значению риска.

Рис. 3.4. Зависимость риска от времени при различных значениях n

3.9. Представление функции риска в виде таблицы

При выполнении предыдущих действий для построения графика на экране было получено выражение риска. Предположим, что оно находится в строке #1. Тогда функцию риска в виде таблицы можно получить путем табулирования функции R_c(t).

В строке пользователя набирается функция табулирования:

TABLE ([t,#2], t, tn, tk, dt),

где t - аргумент функции риска; tn, tk, dt- соответственно начальное, конечное значения времени t и шаг изменения t. В нашем случае tn = 0, tk выбираем равным среднему времени безотказной работы tk = T = 12136 ч.

Выберем шаг таблицы dt = 1500. Тогда функция будет иметь вид:

После ввода функции нужно нажать кнопку «Approximate» панели инструментов. Процедуры табулирования и итоговая таблица при n = 9 на экране монитора имеют следующий вид (рис.3.5):

Рис. 3.5. Процедура табулирования и итоговая таблица

Из строки #4 рис. 3.5 видно, что риск возрастает с увеличением времени функционирования системы t. Так, например, с увеличением t с 1500 д 12 000 часов риск увеличивается примерно с 150 до 800 условных единиц.

3.10. Определение критического времени работы системы

Так как R_c(t) возрастает с ростом t, то представляет интерес предельное время, выше которого риск будет превышать допустимое значение. Решение задачи сводится к определению корня уравнения

.

Так как в рассматриваемом случае , ч.^-1,

R=5000, то, подставляя эти значения в последнее выражение, получим:

.

Решая это уравнение с помощью функции «SOLVE», получим критическое значение τ. В нашем примере вещественного корня нет. Это значит, что при любом t риск системы не превосходит допустимого значения.

3.11. Исследование зависимости G_R(t,n)

Для анализа зависимости G_R(t,n) представим эту функцию в виде графиков и таблиц. Графики позволят сделать качественный анализ, а таблицы — количественный. Далее описываются процедуры представления функций в виде графиков и таблиц с помощью системы Derive 6.

3.12. Построение графиков G_R(t,n)

Предположим, что система состоит из n равно надежных элементов, каждый из которых имеет интенсивность отказов λ. Тогда функция G_R(t,n) будет выражаться формулой (3.3). Подставим в эту формулу значение λ=0,824·10^-5 ч.^-1 и наберем формулу в строке пользователя. Построение графиков осуществляется так, как было описано в ранее. Построим графики для 3—4 значений n, например, для n, 3 n, 5 n, где n - число элементов системы. В итоге получим семейство кривых (рис. 3.6), из которых можно сделать два важных вывода:

1. Чем больше элементов n и чем больше время работы системы, тем больше погрешность приближенной формулы.

2. Приближенной формулой можно пользоваться в том случае, когда время работы системы мало и риск, вычисленный по приближенной формуле, не превышает допустимого значения.

Рис. 3.6. График функции G_R(t,n)

3.13. Представление функции G_R(t,n) в виде таблицы

Представление функции в виде таблицы выполним с помощью функции «VECTOR» в такой последовательности:

Ввести выражение (3.3);

Присвоить переменной λ среднее значение (в нашем примере λ=0,824·10^-5 ч.^-1); присвоение осуществляется с помощью кнопки «Substitute» панели инструментов;

присвоить переменной n значения n = 10, 30, 50. На экране монитора появятся три выражения. Пусть эти выражения находятся на строках #2, #3, #4 (рис 3.7);

ввести функцию:

VECTOR ([t,#2,#3,#4], t, tn, tk, dt).

В нашем примере tn = 0, tk= T₁ =12136, dt = 1500, тогда команда будет иметь вид:

VECTOR([t,#2,#3,#4], t, 0, 12136, 1500);

нажать кнопку «Approximate», на экране появится решение в виде таблицы.

Вычислительные процедуры (рис. 3.7) и итоговая таблица (рис. 3.8) имеют следующий вид:

Рис. 3.7. Вычислительная процедура

Рис. 3.8. Итоговая таблица

 

Из таблицы видно, что функция G_R(t,n) является убывающей. Это означает, что с увеличением времени и увеличением числа элементов погрешность приближенной формулы возрастает.

Определим предельные значения функции G_R(t,n) воспользовавшись кнопкой «Find Limit (lim)» панели инструментов.

Пределы существуют, если переменные n и λ положительны и значение n конечно. Укажем это программе с помощью пункта меню «Author | Variable Domain». Процедура решения представлена на рисунке 3.9.

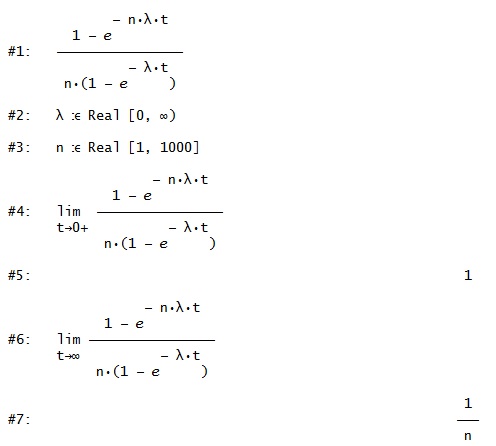
Рис. 3.9. Процедура решения

 

Таким образом, предельное значение погрешности приближенной формулы равно 1/ n.

По результатам выполненной работы необходимо сделать выводы об особенностях надежности работы нерезервированных

ВАРИАНТЫЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ

Вариант 1

Номера элементов
λ 10-5, ч-1	1,1	0,5		4,2	3,6	2,1	4,4	4,8
r, у.е.

Т=1500 ч.,R= 8000 у.е.

Вариант 2

Номера элементов
λ 10-5, ч-1	2,6	3,2	6,4	1,2		1,8	5,1	4,2
r, у.е.

Т=1200 ч.,R= 5000 у.е.

Вариант 3

Номера элементов
λ 10-5, ч-1	0,5	0,2		1,2	0,6	2,1	1,2	0,7
r, у.е.

Т=2500 ч.,R= 3200 у.е.

Вариант 4

Номера элементов
λ 10-5, ч-1	0,2	0,8	2,3	0,1	0,5	1,2	3,4	0,7
r, у.е.

Т=3800 ч.,R= 5000 у.е.

Вариант 5

Номера элементов
λ 10-5, ч-1	1,1	2,3	4,7	0,6		4,8	3,2	2,6
r, у.е.

Т=4000 ч.,R= 4800 у.е.

Вариант 6

Номера элементов
λ 10-5, ч-1	1,2	0,8	1,6	0,2	0,1	0,05	6,2	2,4
r, у.е.

Т=5000 ч.,R= 860 у.е.

Вариант 7

Номера элементов
λ 10-5, ч-1	3,2	0,1		0,7	1,2	0,3	0,1	1,2
r, у.е.

Т=1500 ч.,R= 8000 у.е.

Вариант 8

Номера элементов
λ 10-5, ч-1	1,1	0,5		4,2	3,6	2,1	4,4	4,8
r, у.е.

Т=5000 ч.,R= 860 у.е.

Вариант 9

Номера элементов
λ 10-5, ч-1	2,6	3,2	6,4	1,2		1,8	5,1	4,2
r, у.е.

Т=4200 ч.,R= 3850 у.е.

Вариант 10

Номера элементов
λ 10-5, ч-1	0,5	0,2		1,2	0,6	2,1	1,2	0,7
r, у.е.

Т=4000 ч.,R= 4800 у.е.

Вариант 11

Номера элементов
λ 10-5, ч-1	0,2	0,8	2,3	0,1	0,5	1,2	3,4	0,7
r, у.е.

Т=2500 ч.,R= 3200 у.е.

Вариант 12

Номера элементов

Поделиться: