Математика, 22.10.20. гр.24, занятие № 26-27-28
Тема: Анализ контрольной работы Работа над ошибками. Прямоугольная система координат в пространстве. Координаты точки и координаты вектора.
Цель: Ознакомить с прямоугольной системой координат в пространстве. Научить определять координаты точки и координаты вектора в пространстве.
План.
1.Работа над ошибками.Решение примеров 2. Прямоугольная система координат в пространстве3. Домашнее задание
1. Решение примеров.
1.Угол 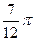 принадлежит:
принадлежит:
а) 1 четверти; б) 2 четверти; в) 3 четверти; г) 4 четверти;
2. В прямоугольном треугольнике АВС найти 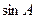 :
:
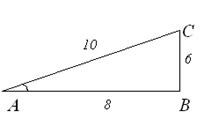
а) 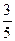 ; б)
; б) 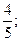 в)
в) 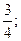 д)
д) 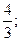
3. Указать верное равенство:
а) 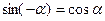 ; б)
; б) 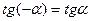 ;
;
в) 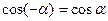 ; г)
; г) 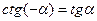 ;
;
4. Указать неверное равенство:
а) 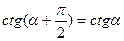 ; б)
; б) 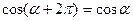 ;
;
в) 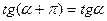 ; г)
; г) 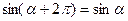 ;
;
5. График какой функции изображен на рисунке*
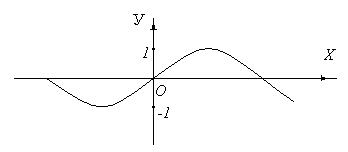
а) 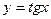 ; б)
; б) 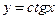 ; в)
; в) 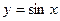 ; г)
; г) 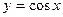
Теоретический материал для самостоятельного изучения
Прямоугольная система координат в пространстве
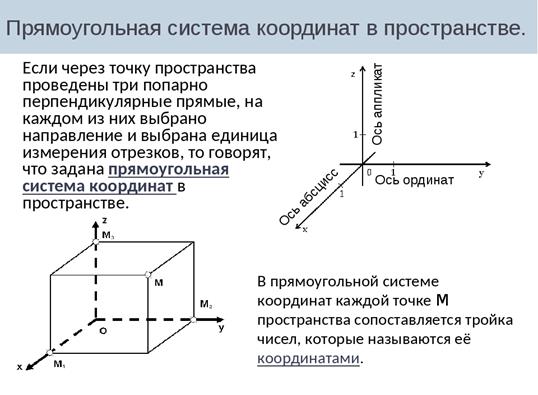
| Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве. Прямые с выбранными на них направлениями называются осями координат, а их общая точка —началом координат. Она обозначается обычно буквой О. Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат. Вся система координат обозначается Охуz. Плоскости, проходящие соответственно через оси координат ОхиОу, ОуиОz, ОzиОх, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх. Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью. |
В прямоугольной системе координат каждой точке А пространства сопоставляется тройка чисел, которые называются ее координатами. Они определяются аналогично координатам точек на плоскости. Вы уже знакомы с прямоугольной системой координат на плоскости, другими словами прямоугольной координатной плоскостью. Такую систему координат задают две взаимно перпендикулярные прямые, на каждой из которых выбрано направление и величина единичного отрезка. Эти прямые называют осями абсцисс и ординат. Каждой точке плоскости сопоставляется только одна пара чисел, которые называют её координатами. Для определения координат, из точки нужно провести перпендикуляры к осям, тем самым мы и получим абсциссу и ординату точки.



Свойства векторов, заданных координатами
- Координаты нулевого вектора равны нулю.
- Координаты равных векторов соответственно равны.
- Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов.
- Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов.
- Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.
Формулы
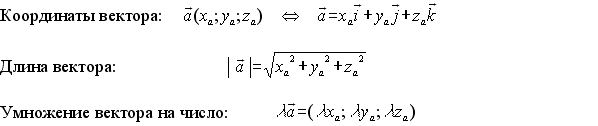
Основной учебник:
Л.С. Атанасян, В.Ф.Бутузов, Геометрия 10-11, учеб. для общеобразовательных учреждений.– М. Просвещение, 2016
Домашнее задание: гл. 4 п46-48.с102-105. Составить конспект урока, Решить задачи:
1. Определите, лежит ли данная точка на координатной оси. Если да, то укажите эту ось. 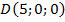 ,
, 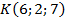 ,
, 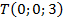 ,
, 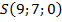 ,
, 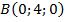 (см. таблицу внизу)
(см. таблицу внизу)
2. Определите, принадлежит ли данная точка координатной плоскости. Если да, то назовите ее. 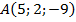 ,
, 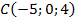 ,
, 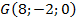 ,
, 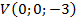 ,
, 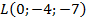 .
.

Результат в виде файла в формате Word направить преподавателю на yptu45@mail. ru
Также в группы 24 гр. https://vk.com/club194181059