98. Механическая характеристика материала листа, для определения силы, необходимая для продавливания отверстий
1. Предел текучести
2. Предел прочности на растяжение
3. Предел прочности на срез
99. Указать напряженное состояние,которое называется «чистым сдвигом»
1. 1
2. 2
3. 3
4. 4
Тема 5. Кручение
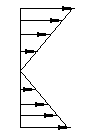
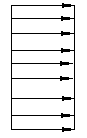
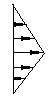
100. Выбрать эпюру распределения напряжений в поперечном сечении бруса при кручении
R kbixZCWbRmk6TSCuIDZA4pY1XlvROFWTreXfY07s5mc/PX+v2Ey+E2ccYhvIwGKuQCBVwbVUG3jf P9+uQcRkydkuEBr4wQibcnZV2NyFkd7wvEu14BCKuTXQpNTnUsaqQW/jPPRIfDuGwdvEcqilG+zI 4b6TmVIr6W1L/KGxPT42WH3vTt7Ax8vx61Or1/rJL/sxTEqSv5fG3FxP2wcQCaf0b4Y/fEaHkpkO 4UQuio71WnGXZCBbaA2CHdmd5s2Bh6XSIMtCXnYofwEAAP//AwBQSwECLQAUAAYACAAAACEAtoM4 kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAI AAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAI AAAAIQC91ReBxAIAAMIFAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQA BgAIAAAAIQBOB37+3gAAAAsBAAAPAAAAAAAAAAAAAAAAAB4FAABkcnMvZG93bnJldi54bWxQSwUG AAAAAAQABADzAAAAKQYAAAAA " filled="f" stroked="f">
1 2 3 4 5
Тема 6. Изгиб
101. В поперечном сечении балки возникли изгибающий момент и поперечная сила. Указать вид изгиба.
1. Чистый изгиб
2. Поперечный изгиб
102. Изменение величины и знака поперечной силы и изгибающего момента, при вычислении их по внешним силам, расположенным слева или справа от сечения
1. Изменяются
2. Не изменяются
103. Поперечные силы сечений на расстоянии от концов балок выражены уравнениями: Q1 = - F; Q2 = - F + q·z. Указать, какими линиями очерчены эпюры поперечных сил
1. В обоих случаях наклонными прямыми линиями
2. В первом случае — прямой, параллельной оси балки, во втором — прямой, наклоненной к оси балки
104. Изгибающие моменты в сечении на расстоянии от концов балок выражены уравнениями: М1= VA·х; M2 = m. Указать, какими линиями очерчены эпюры изгибающих моментов.
1. В обоих случаях наклонными прямыми линиями
|
|
2. В первом случае — прямой, наклоненной к оси, во втором — прямой, параллельной оси
105. Указать, какими линиями очерчена эпюра изгибающих моментов, если закон их изменения по длине балки выражается уравнением
Мих= q·x2 /2
1. Наклоненной к оси
2. Прямой
3. В виде параболы
106. 
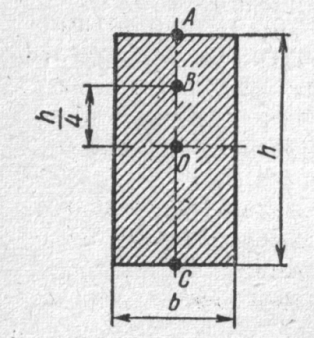Точка поперечного сечения балки,на которой возникает наибольшие нормальные напряжения
1. Точка А
2. Точка О
3. Точка В
107. Указать, для какой точки на рисунке поперечного сечения балки нормальные напряжения могут быть вычислены по формуле
1. Для точки О
2. Для точки В
3. Для точек А и С
108. Указать вкаком из двух вариантов нагружения(а или б) двутавровая балка сможет выдержать большую силу Р. Длина консолей l в обоих случаях одинакова.
1. В случае, изображенном на рисунке а)
2. В случае, изображенном на рисунке б)
3. В обоих случаях балка может выдержать одинаковую нагрузку
109. Балки, изготовленные из стали и чугуна, имеющие одинаковые размеры и устройство опор, подвергаются действию одинаковых сил. Сравнить величину максимальных прогибов этих балок.
1. У стальной балки прогиб больше
2. У чугунной балки прогиб больше
3. Прогиб балок одинаковый
110. Условие возникновения изгибающего момента в сечениях вала, если на валу закреплены зубчатые колеса. К зубьям колес приложены окружные силы Р1 и Р2.
1. Вал будет работать только на кручение
2. Вал будет работать на изгиб и кручение
111. Устойчивая форма стержня, когда величина сжимающей силы больше критической
1. Прямолинейная
2. Криволинейная
112. Возможность установленияизлома по внешнему виду, напряжения при которых работала деталь, когда излом имеет две зоны: одну гладкую притертую и другую - грубо зернистую
|
|
1. Деталь работала при постоянных напряжениях
2. Деталь работала при переменных напряжениях