Задача о загрузке оборудования
Завод располагает двумя видами станков, из них 20 станков типа 1 и 25 станков типа 2. Станки могут производить 3 вида продукции: П1, П2, П3 с разной производительностью. Например, станок 1 типа производит (в смену) a 11 продукции П1, a 12 продукции П2 и т.д. (первый индекс – тип станка, второй – вид продукции). Производительность станков при производстве каждого вида продукции задана таблицей.
| Тип станков | Вид продукции | Кол-во станков, не более | ||
| П1 | П2 | П3 | ||
  a 11 = 12
a 21 = 17
| a 12 = 10 a 22 = 14 | a 13 = 13 a 23 = 16 | ||
| Доход – max | ||||
| План, не менее |
По плану завод должен производить (в смену) не менее 200 единиц продукции типа П1, 150 ед. – типа П2 и 220 ед. – типа П3.
Каждая единица продукции 1-го, 2-го и 3-го типов приносит заводу доход соответственно 5, 3 и 7 условных единиц.
Требуется так распределить загрузку станков производством продукции различного типа, чтобы план был выполнен и при этом прибыль была максимальна.
За x принимается не продукция, а станки.
Пусть xij – число станков i -го типа, занятых на производстве продукции j -го типа (i = 
; j = 
). Т.е. имеется 6 переменных, которые мы должны выбрать так, чтобы прибыль была максимальной.
Т. к. плановые задания должны быть выполнены или перевыполнены, то принимаются ограничения по выпуску продукции и по числу занятых станков:
Целевая функция должна обеспечивать максимальный доход от производства всех видов продукции, т.е.
max z = 5(12 x 11 + 17 x 21) + 3(10 x 12 + 14 x 22) + 7(13 x 13 + 16 x 23)
Ответ: max z = 3552,35; x 11 = x 12 = 0; x 13 = 20; x 21 = 11,76; x 2 2 = 10,7;
x 23 = 2,52.
Дополнительные ограничения
Если перевыполнение плана ограничено, чтобы не было затоваривания продукции, то вводятся дополнительные ограничения. Например, нельзя производить более 250 ед. продукции вида 1, 200 ед. вида 2, 260 ед. вида 3.
Тогда вводятся дополнительные ограничения
(3)
При условии обязательной загрузки всего оборудования ограничения по числу используемых станков из неравенств станут равенствами, т. е
(4) вместо (2)
Ответ: max z = 3484,2; x 11 = x 12 = x 23 = 0; x 13 = 20; x 21 = 14,3; x 22 = 10,7.
Целочисленное линейное программирование
Экстремальная задача, переменные которой принимают лишь целые значения, называется задачей целочисленного программирования.
В математической модели задачи ЦЛП, как целевая функция, так и функции в системе ограничений могут быть линейными и нелинейными. Рассмотрим пример для линейного случая.
Графическое решение задач ЦЛП
Пример. (Акулич, с. 176)
В цехе надо установить оборудование, для размещения которого выделено 19/3 м2 площади. На приобретение оборудования можно израсходовать 10 тыс. руб., при этом можно купить оборудование двух видов: I и II. Оборудование I вида стоит 1 тыс. руб., а II вида – 3 тыс. руб. Приобретение оборудования I вида позволит увеличить выпуск продукции в смену на 2 единицы, а II вида – на 4 единицы. Для установки одного оборудования I вида требуется 2 м2, II вида – 1 м2.
Требуется определить набор оборудования, который позволит максимально увеличить выпуск продукции.
Решение:
Составим математическую модель задачи.
Примем, что предприятие приобретает x 1 оборудования I вида и x 2 – II вида. Тогда x 1 и x 2 должны удовлетворять неравенствам:
I II
2 x 1 + x 2 ≤ 19/3 м2, (1)
x 1 + 3 x 2 ≤ 10 тыс. руб. (2)
x 1 ≥ 0; x 2 ≥ 0.
Увеличение выпуска продукции составит (целевая функция):
z = 2 x 1 + 4 x 2 → max.
При этом
x 1, x 2 ³ 0,
x 1, x 2 – целые.
Это задача ЦЛП.
Решим задачу графически.
Координаты всех точек многоугольника ОАВС удовлетворяют условию неотрицательности переменных. Максимум z в точке В (1,8; 2,73).
Нельзя округлять, например, x 1=2, x 2=3, т.к. не выполняются ограничения.
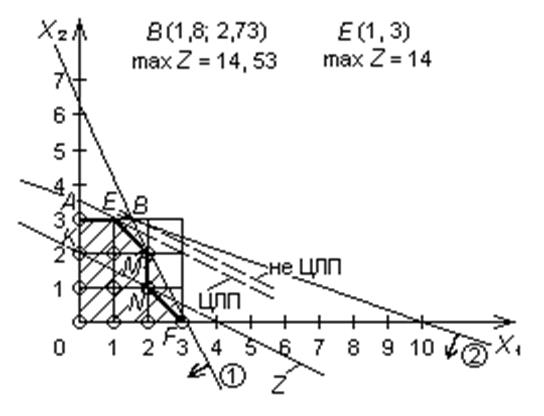
Условию целочисленности удовлетворяют координаты лишь 12 точек многоугольника OKENMF, среди которых надо найти точку максимума функции, которая определяет оптимильный план задачи.
Перемещаем линию целевой функции z, пока она не пройдет через последнюю общую с многоугольником точку Е. Полученное решение: x 1=2, x 2=3, а z =14 ед. (Проверить соседние вершины К и М).
Метод ветвей и границ
Аналитическое решение возможно методами: Гомори и ветвей и границ.
Метод ветвей и границ представляет собой процедуру перебора всех целочисленных допустимых решений.
Последовательность решения задач ЦЛП:
Шаг 1. Решается задача ЛП-1 и находится значение целевой функции z 1. Если переменные xi принимают дробные значения, то оптимальное решение целочисленной задачи не совпадают с решением ЛП-1 и величина z 1 является верхней границей оптимального значения целочисленной задачи. (в примере было z =14,53).
Шаг 2. Производится ветвление по одной из переменных, имеющей дробное значение в задаче ЛП-1 по следующему правилу:
1) выбирается переменная, имеющая наибольшее дробное значение;
2) если дробные значения одинаковые, то выбирается переменная, коэффициент при которой в целевой функции наибольший.
Определяются два допустимых целых значения переменной xi, удовлетворяющих одному из неравенств:
xi £ [ xi ]; xi ³ [ xi ] + 1,
где [] – целая часть дроби.
Исходная задача разветвляется на две подзадачи: ЛП-2 и ЛП-3, каждая из которых решается.
Шаг 3
1 ) Если одно из полученных решений оказывается допустимым для целочисленной задачи, то значение целевой функции z является начальной нижней границей оптимального значения.
2)Если решения дробные, то для дальнейшего ветвления выбирают вершину, соответствующую наибольшему значению целевой функции.
В процессе решения отбрасываются все подзадачи, в которых значение z хуже начального. Такие подзадачи называются прозондированными.
Процесс ветвления продолжается до тех пор, пока не будут прозондированы все подзадачи и установлена невозможность улучшения (нижней границы) решения.
Пример.
max z = 3 x 1 + 2 x 2,
x 1 + x 2 ≤ 3,5,
x 1 ≤ 2; x 2 ≤ 2,
x 1, x 2 ≥ 0, целые.
Шаг 1. Решается задача ЛП-1.
Верхняя граница целевой функции z 1 = 9
Шаг 2. Т.к. x 2 =1,5 дробное, то просматриваются его целочисленные значения при x 2 £1 и x 2 ³2.
Шаг 3. 1) Решая ЛП-2, находим при x 2 = 1 начальное целочисленное решение. Значение z 2 = 8 является нижней границей.
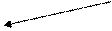
2) Решая ЛП-3, при x 2 = 2, значение x 1 = 1,5 – дробное, что недопустимо.
Т.к. z 3 = 8,5 > z 2 = 8, то проверяется наличие (зондируем) в допустимой области задачи ЛП-3 целочисленного решения, дающего значение z ³ 8.
Рассмотрим задачи ЛП4 и ЛП5 при целых значениях x 1:
а) при x 1 = 1 решение ЛП-4 целочисленное, но z 4 = 7 < z 2 = 8;
б) при x 1 = 2 нет допустимых решений.
Т.о. точка x 1 = 2, x 2 = 1 является оптимальным целочисленным решением задачи и значение целевой функции равно z = 8.
Шаг 1. ЛП-1.
x 1 = 2, x 2 =1,5, z 1 =9 (верхняя граница)
Шаг 2
ЛП2 ЛП3
x 2 £ 1 x 2 ³ 2
x 1 = 2, x 2 = 1, z 2 = 8 x 1 = 1,5, x 2 = 2, z 3 = 8,5
Решение начальное (нижняя граница) z 3³ z 2
Оптимум
ЛП-4 ЛП-5
x 1 £ 1 x 1 ³ 2
нет допустимых решений
x 1 = 1, x 2 = 2, z 4 = 7
Решение (не оптимум)