Практические заНЯТИя
Цель: освоить применение классического (графо-аналитического) метода расчета цепей гармонического тока. Получить навыки построения векторных диаграмм и их использования для расчета цепей синусоидального тока.
 Задача 1. В сеть с переменным напряжением
Задача 1. В сеть с переменным напряжением 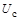 = 220 В включается электрическая лампа, номинальное напряжение которой
= 220 В включается электрическая лампа, номинальное напряжение которой 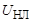 =
=
= 127 В, мощность 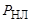 = 60 Вт. Для «погашения» части напряжения последовательно с лампой включается конденсатор. Определить необходимую емкость конденсатора, если f = 50 Гц.
= 60 Вт. Для «погашения» части напряжения последовательно с лампой включается конденсатор. Определить необходимую емкость конденсатора, если f = 50 Гц.
Решение
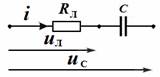
В схеме замещения электрической цепи (см. рисунок) лампа представляется активным сопротивлением 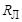 .
.
Мощность лампы определяется выражением
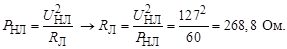
Ток в электрической цепи
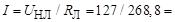 0,472 A.
0,472 A.
Модуль полного сопротивления цепи
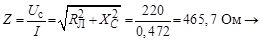
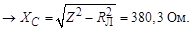
Величина емкости конденсатора
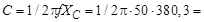 8,3 мкФ.
8,3 мкФ.
Ответ: 8,3 мкФ.
Задача 2. Цепь состоит из последовательного соединенных активного сопротивления, индуктивности L = 0,142 Гн и емкости С. Напряжение на зажимах цепи 120 В, ток цепи 4 А, активная мощность 240 Вт, частота 50 Гц.
Определить величины активного сопротивления и емкости. Объяснить, почему существует два значения емкости, удовлетворяющих условию.
Решение
Модуль полного сопротивления цепи
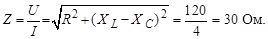
Активное сопротивление цепи
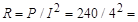 15 Ом.
15 Ом.
Реактивное сопротивление индуктивности
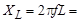 44,6 Ом.
44,6 Ом.
Реактивное сопротивление цепи
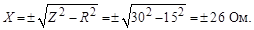
Реактивное емкостное сопротивление
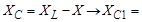 18,6 Ом;
18,6 Ом;  70,6 Ом.
70,6 Ом.
Значения емкости:
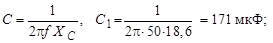
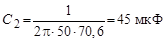 .
.
Получены два значения величины емкости, удовлетворяющие условию, это объясняется тем, что сопротивление цепи с Z = 30 Ом может иметь как активно-индуктивный характер, так и активно емкостный (R = 15 Ом, X = ±26 Ом).
Ответ: 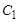 = 171 мкФ;
= 171 мкФ; 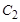 = 45 мкФ.
= 45 мкФ.
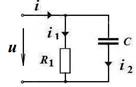 Задача 3. Две параллельные ветви подключены к источнику синусоидального напряжения. Определить напряжение u, токи i и
Задача 3. Две параллельные ветви подключены к источнику синусоидального напряжения. Определить напряжение u, токи i и 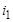 , если
, если 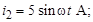 R = 10 Ом;
R = 10 Ом; 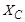 = 10 Ом.
= 10 Ом.
Решение
Построим векторную диаграмму токов и напряжений для заданной схемы. Последовательность построения 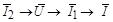 .
.
Вектор тока 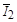 имеет длину
имеет длину 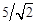 и расположен горизонтально (начальная фаза равна нулю).
и расположен горизонтально (начальная фаза равна нулю).
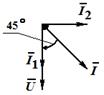 Вектор напряжения на емкости (входного напряжения)
Вектор напряжения на емкости (входного напряжения) 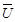 имеет длину
имеет длину 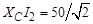 и отстает от вектора тока
и отстает от вектора тока 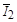 на угол 90°. Вектор тока через резистор
на угол 90°. Вектор тока через резистор 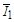 совпадает по направлению с вектором напряжения и имеет длину
совпадает по направлению с вектором напряжения и имеет длину 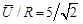 . Вектор входного тока
. Вектор входного тока 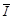 определяется как сумма векторов токов через резистор
определяется как сумма векторов токов через резистор 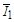 и емкость
и емкость 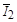 . Векторы имеют равную длину
. Векторы имеют равную длину 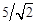 и расположены относительно друг друга под прямым углом. Следовательно, длина вектора
и расположены относительно друг друга под прямым углом. Следовательно, длина вектора 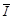 равна 5 А и опережает вектор входного напряжения на угол 45°.
равна 5 А и опережает вектор входного напряжения на угол 45°.
В соответствии с векторной диаграммой записываем мгновенные значения искомых величин:
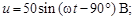
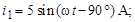
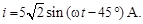
Ответ: 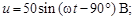
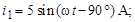
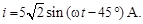
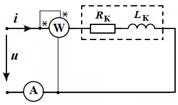
Задача 4. Катушка индуктивности подключена к сети с напряжением U = 100 В. Ваттметр показывает значение 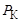 = 600 Вт, амперметр – значение I = 10 А. Определить параметры катушки
= 600 Вт, амперметр – значение I = 10 А. Определить параметры катушки 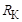 ,
, 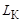 .
.
 Решение
Решение
Вычисляем модуль полного сопротивления катушки:
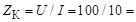 10 Ом.
10 Ом.
По показаниям ваттметра и амперметра определяем активное сопротивление катушки 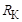 . Ваттметр, включенный на входе цепи, измеряет потребляемую цепью активную мощность, которая в данной схеме потребляется активным сопротивлением
. Ваттметр, включенный на входе цепи, измеряет потребляемую цепью активную мощность, которая в данной схеме потребляется активным сопротивлением 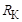 :
:
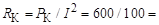 6 Ом.
6 Ом.
Зная величину модуля полного сопротивления катушки и ее активное сопротивление, из треугольника сопротивлений определяем реактивное сопротивление катушки 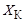 :
:
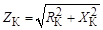 ;
; 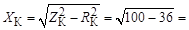 8 Ом.
8 Ом.
Найдем индуктивность катушки 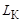 :
:
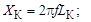
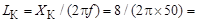 0,025 Гн.
0,025 Гн.
Ответ: 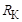 = 6 Ом;
= 6 Ом; 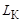 = 0,025 Гн.
= 0,025 Гн.
Задача 5. К электрической сети напряжением U = 220 В и частотой f = 50 Гц подключены параллельно два электроприбора, потребляющие активные мощности 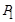 = 0,3 кВт и
= 0,3 кВт и 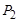 = 0,4 кВт, имеющие коэффициенты мощности
= 0,4 кВт, имеющие коэффициенты мощности 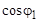 = 0,6 и
= 0,6 и 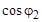 = 0,7 соответственно, и электропечь мощностью
= 0,7 соответственно, и электропечь мощностью 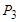 = 0,5 кВт.
= 0,5 кВт.
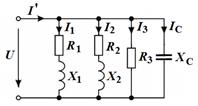
1. Начертить электрическую схему замещения цепи.
2. Определить токи каждого устройства и ток, потребляемый схемой от сети, ее активную, реактивную и полную мощности.
3. Определить емкость конденсатора, подключаемого параллельно нагрузке для повышения 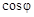 цепи до значения 0,9, рассчитать ток, потребляемый схемой от источника в этом режиме.
цепи до значения 0,9, рассчитать ток, потребляемый схемой от источника в этом режиме.
Решение
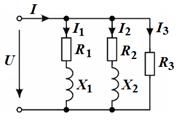 1. Схема замещения каждого электрического прибора может быть представлена в виде последовательного соединения резистивного и индуктивного элементов, так как в приборе происходит необратимое преобразование электрической энергии в механическую и тепловую и колебательный обмен энергией между магнитным полем потребителей и сетью. Схема замещения электропечи представляется активным сопротивлением. Схема замещения всей цепи показана на рисунке.
1. Схема замещения каждого электрического прибора может быть представлена в виде последовательного соединения резистивного и индуктивного элементов, так как в приборе происходит необратимое преобразование электрической энергии в механическую и тепловую и колебательный обмен энергией между магнитным полем потребителей и сетью. Схема замещения электропечи представляется активным сопротивлением. Схема замещения всей цепи показана на рисунке.
2. Токи устройств рассчитываются по паспортным данным:
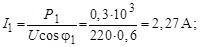
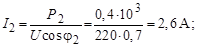
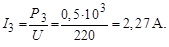
Сдвиги токов ветвей по фазе по отношению к напряжению:
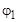 = 53,1°;
= 53,1°; 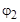 = 45,5°;
= 45,5°; 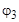 = 0°.
= 0°.
Активная мощность цепи
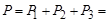 300 + 400 + 500 = 1200 Вт.
300 + 400 + 500 = 1200 Вт.
Реактивные мощности электроприборов:
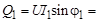 220 × 2,27 × 0,8 = 399 вар;
220 × 2,27 × 0,8 = 399 вар;
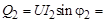 220 × 2,6 × 0,713 = 407 вар.
220 × 2,6 × 0,713 = 407 вар.
Реактивная мощность цепи
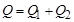 = 399 + 407 = 806 вар.
= 399 + 407 = 806 вар.
Полная мощность цепи
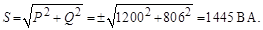
Ток, потребляемый схемой от сети,
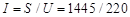 = 6,57 А.
= 6,57 А.
Коэффициент мощности схемы
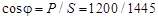 = 0,83.
= 0,83.
3. Рассчитаем емкость конденсатора, необходимую для повышения коэффициента мощности нагрузки сети до 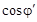 = 0,9.
= 0,9.
 Включение конденсатора параллельно нагрузке не изменяет ее активную мощность, но позволяет уменьшать реактивную и полную мощность, потребляемую всей схемой от источника. Поэтому по активной мощности цепи и заданному значению
Включение конденсатора параллельно нагрузке не изменяет ее активную мощность, но позволяет уменьшать реактивную и полную мощность, потребляемую всей схемой от источника. Поэтому по активной мощности цепи и заданному значению 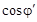 определим полную мощность цепи:
определим полную мощность цепи:
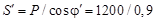 = 1333 ВА.
= 1333 ВА.
Реактивная мощность цепи
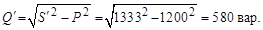
Реактивная мощность всей цепи равна алгебраической сумме реактивных мощностей ее участков. В данном случае 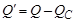 , поэтому мощность конденсатора
, поэтому мощность конденсатора
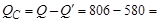 226 вар.
226 вар.
Ток в цепи конденсатора и его сопротивление:
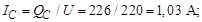
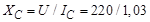 = 214 Ом.
= 214 Ом.
Емкость конденсатора
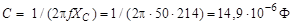 = 14,9 мкФ.
= 14,9 мкФ.
Результирующий потребляемый цепью ток при подключении к нагрузке компенсирующей емкости
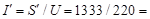 6,06 А.
6,06 А.
Ответ: 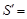 1333 ВА;
1333 ВА; 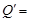 580 вар;
580 вар; 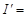 6,06 А.
6,06 А.
Задача 6. Известны показания амперметров:
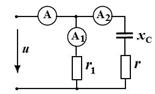
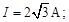
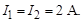
Определить значения R и 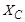 ; коэффициент мощности цепи
; коэффициент мощности цепи 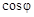 , если
, если 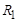 = 50 Ом.
= 50 Ом.
Решение
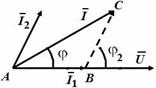 Построим векторную диаграмму для заданной цепи. Построение начинаем с вектора входного напряжения, так как имеем параллельное соединение ветвей. Вектор тока
Построим векторную диаграмму для заданной цепи. Построение начинаем с вектора входного напряжения, так как имеем параллельное соединение ветвей. Вектор тока 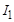 совпадает по направлению с вектором входного напряжения, так как сопротивление ветви чисто активное. Вектор тока
совпадает по направлению с вектором входного напряжения, так как сопротивление ветви чисто активное. Вектор тока 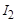 опережает вектор входного напряжения, потому что ветвь носит активно-емкостный характер. Вектор входного тока
опережает вектор входного напряжения, потому что ветвь носит активно-емкостный характер. Вектор входного тока 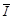 равен сумме векторов токов параллельных ветвей
равен сумме векторов токов параллельных ветвей 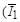 и
и 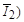 в соответствии с первым законом Кирхгофа.
в соответствии с первым законом Кирхгофа.
Векторы токов образуют треугольник АВС. Применив теорему косинусов, определим угол АВС (ψ):
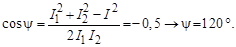
Угол разности фаз между входным напряжением и током 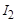
(в r – C ветви)
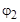 = 180° – ψ = 60°.
= 180° – ψ = 60°.
Модуль полного сопротивления r – C ветви
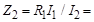 50 Ом.
50 Ом.
Активная составляющая сопротивления 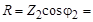 25 Ом, емкостное сопротивление ветви
25 Ом, емкостное сопротивление ветви 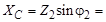 43,3 Ом.
43,3 Ом.
Определим коэффициент мощности цепи. Треугольник АВС равнобедренный 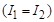 , следовательно, угол разности фаз (между векторами входного напряжения и входного тока) φ = 30°. Коэффициент мощности цепи
, следовательно, угол разности фаз (между векторами входного напряжения и входного тока) φ = 30°. Коэффициент мощности цепи 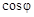 = 0,866.
= 0,866.
Ответ: R = 25 Ом; 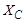 = 43,3 Ом;
= 43,3 Ом; 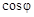 = 0,866.
= 0,866.
Дополнительные задачи
Задача 1. В последовательном контуре с реальной катушкой индуктивности (R = 50 Ом; L = 20 мГн) и конденсатором (C = 1 мкФ) задан ток 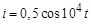 A.
A.
Определить мгновенные значения напряжений на катушке и на входе цепи.
Ответ: 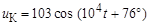 B;
B; 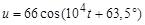 B.
B.
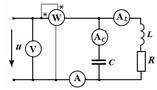 Задача 2. Определить показания амперметров (электромагнитной системы) и ваттметра, если вольтметр показывает 100 В;
Задача 2. Определить показания амперметров (электромагнитной системы) и ваттметра, если вольтметр показывает 100 В;
f = 50 Гц; R = 10 Ом; L = 0,2 Гн; С = 40 мкФ.
Ответ: I = 0,388 A, 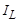 = 1,57 А,
= 1,57 А,  =
=
= 1,25 А, P = 27,3 Вт.
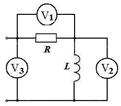 Задача 3. В цепи R – L известны показания вольтметров
Задача 3. В цепи R – L известны показания вольтметров 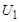 = 100 В;
= 100 В; 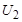 = 150 Ви сопротивление R = 10 Ом. Определить показание третьего вольтметра и индуктивность, если частота тока
= 150 Ви сопротивление R = 10 Ом. Определить показание третьего вольтметра и индуктивность, если частота тока
f = 50 Гц.
Ответ 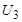 = 180 В; L = 47,7 мГн.
= 180 В; L = 47,7 мГн.
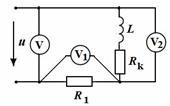 Задача 4. Вольтметры электромагнитной системы показывают: V = 220 В,
Задача 4. Вольтметры электромагнитной системы показывают: V = 220 В, 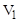 = 110 В,
= 110 В, 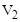 = 138 В. Определить параметры катушки индуктивности, если сопротивление
= 138 В. Определить параметры катушки индуктивности, если сопротивление 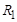 = 22 Ом.
= 22 Ом.
Ответ: 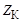 = 27,6 Ом;
= 27,6 Ом; 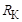 = 16,63 Ом;
= 16,63 Ом; 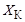 = 22,75 Ом.
= 22,75 Ом.
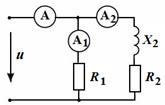
Задача 5. Показания амперметров электромагнитной системы: 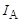 = 6,5 А;
= 6,5 А;
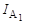 = 4 А;
= 4 А; 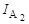 = 3,5 А. Определить мощность, расходуемую катушкой индуктивности
= 3,5 А. Определить мощность, расходуемую катушкой индуктивности 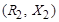 , если сопротивление резистора
, если сопротивление резистора 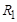 = 30 Ом.
= 30 Ом.
Ответ: S =780 ВА; P = 690 Вт; Q = 364 вар.