Для нахождения оптимального решения задачи в зависимости от вида и структуры целевой функции и ограничений используются следующие методы теории оптимальных решений (методы математического программирования):
1)Линейное программирование – если функции f(Х,Y,A,Q) линейные относительно переменных Х.
2)Нелинейное программирование – если функции f(Х,Y,A) не линейны относительно переменных Х.
3) Дискретное программирование, если на управляющие переменные наложено условие дискретности, например, целочисленности.
4) Динамическое программирование, если функция f(Х,Y) имеет специальную структуру и являются аддитивной или мультипликативной от переменной Х.
А также геометрическое, стохастическое, нечеткое математическое, эвристическое программирование.
Исходя из формализации задачи, определяется вид и структура целевой функции. Функции f(Х,Y,A,Q) являются линейными относительно переменных Х, значит метод решения – линейное программирование.
Поиск решения на модели:
Из постановки задачи следует, что общая функция расходов за период будет иметь следующий вид:
 . (1)
. (1)
Как следует из рис. 1, текущий уровень запасов описывается так:
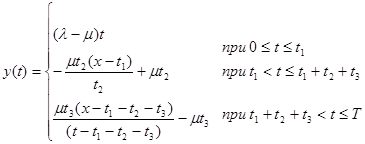
Максимальный дефицит Yg выражается через Y (рис. 1)
 . (1.1)
. (1.1)
Находим  и
и  , тогда
, тогда
 . (2)
. (2)
Обозначим
 , (3)
, (3)
Получим
 . (4)
. (4)
Подставляя (4) в (1.1), получаем
 (5)
(5)
Найдем выражение для функции затрат с учетом (4), (5):
 . (6)
. (6)
Для нахождения средних затрат в единицу времени, поделим функцию затрат LT на период времени Т:
 . (7)
. (7)
Теперь нужно найти такие значения Y0, T0, для которых функция Lср минимальна. Для этого составляем и решаем систему уравнений из частных производных функции средних затрат в единицу времени Lср по предельному запасу Y и по периоду времени Т:

Получим из первого уравнения системы и приравняем к нулю:
 . (8)
. (8)
Из второго аналогично:
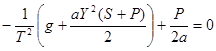 . (9)
. (9)
Из (8) получим такое соотношение
 . (10)
. (10)
Наконец, из (9) получим
 . (11)
. (11)
Подставляя в уравнение (11) выражение для Т из (10), после несложных преобразований получим
 (12)
(12)
Подставив в (12) выражение для a из (3) и поделив числитель и знаменатель на λР, получим окончательное выражение для оптимального уровня запаса
 ; (13)
; (13)
Подставив это выражение в (10), находим оптимальный период поставки
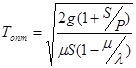 . (14)
. (14)
При таких значениях Y0, T0, достигается минимум средних расходов в единицу времени:
 . (15)
. (15)
Рассмотрим теперь частные случаи общей задачи:
1)недостаток запасов недопустим (см. рис. 3).

Рис. 3. График изменения запасов в случае, когда недостаток запасов не допустим
Если дефицит запасов недопустим значит, что удельный штраф за дефицит единицы продукта в единицу времени Р = ∞ и подставив S/P =0 в (13) - (15), получим:
 , (16)
, (16)
 ,(17)
,(17)
 ; (18)
; (18)
2) мгновенные поставки (рис. 4).

Рис. 4. График изменения запасов при мгновенных поставках
Мгновенные поставки означают, что λ = ∞ и μ/λ = 0. Теперь подставим в уравнения (13) - (15), получим
 , (19)
, (19)
 ,(20)
,(20)
 ; (21)
; (21)
3)дефицит не допускается, поставки мгновенные (рис. 5).

Рис. 5. График изменения запасов в случае, когда не допускается дефицит и поставки мгновенные
Данный частный случай является комбинированным из первого и второго пунктов, которые рассмотрены выше. Подставив Р = ∞ и S/P =0, λ = ∞ и μ/λ = 0 в (13) - (15), получим
 , (22)
, (22)
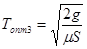 ,(23)
,(23)
 ; (24)
; (24)
Соотношения (22) – (24) называются формулами Уилсона, а (22) - экономическим размером партии.