1. Цель работы: Ознакомиться с законами электромагнитной индукции. Определить индуктивность катушки и сдвига фаз между током и напряжением.
Теоретическая часть.
Основной характеристикой магнитного поля является магнитная индукция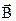 
, определяемая наибольшей величиной вращательного момента, действующего на рамку с током, помещенную в исследуемую точку пространства. Величина
Ф = В S соs α (1)
называется потоком магнитной индукции через некоторую реальную или воображаемую площадку S, расположенную в данном месте. По отношению к силовым линиям индукции магнитного поля (касательные к ним совпадают с векторами 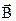) площадка ориентирована под углом α (рис. 1).
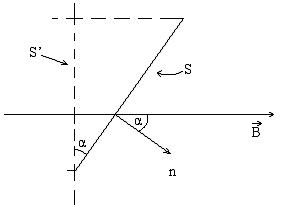
Рис.1
На рисунке 1 S1 = S соs α – проекция S на направление перпендикулярное 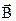. Обычно под α имеют в виду угол между силовой линией 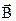и нормалью n (перпендикуляром к площадке S).
В 1931 г. М.Фарадей опытным путем установил, что во всяком замкнутом проводящем контуре при изменении потока магнитной индукции dФ/dt через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление назвали электромагнитной индукцией, возникающей ток – индукционным, а вызвавшую этот ток электродвижущую силу - электродвижущей силой индукции ε1. В соответствии законом Фарадея
εί = –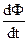 
(2)
Как известно, вокруг любого проводника с током возникает магнитное поле, силовые линии индукции которого совпадают с окружностями, а их направления определяют по правилу правого винта (рис. 2а).
Рис.2
Следовательно, вокруг замкнутого контура с индукционным током также возникает и магнитное поле (рис. 2б) Это поле может усиливать или ослаблять магнитный поток, пронизывающий площадку, ограниченную контуром. Знак «-» в законе Фарадея (2) указывает на то, что индукционный ток в контуре направлен таким образом, чтобы его магнитное поле противодействовало изменению магнитного потока, вызвавшего этот индукционный ток (правило Ленца).
|
|
Частным случаем электромагнитной индукции является самоиндукция. Она возникает при отсутствии внешнего источника изменяющегося магнитного поля. Причиной её появления служит изменяющийся ток, который пропускают через этот же замкнутый контур. Такой ток порождает изменяющееся магнитное поле, а следовательно, и поток магнитной индукции через площадь, ограниченную контуром (рис. 2б). Поэтому в контуре возникает электродвижущая сила индукции или, применительно к настоящему случаю, электродвижущая сила самоиндукции εs.
По закону Био - Савара - Лапласа магнитная индукция 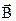прямопропорциональна силе тока J, вызывающей это магнитное поле. Однако в соответствии с формулой (1) магнитный поток Ф в свою очередь прямопропорционален указанной магнитной индукции (1). Следовательно, магнитный поток прямопропорционален также и величине тока в данном контуре:
Φ = L J, (3)
где L – коэффициент пропорциональности, который называют коэффициентом самоиндукции или индуктивностью.
Дифференциал магнитного потока равен:
dΦ = LdJ. (4)
Подставляя выражение дифференциала (4) в закон Фарадея (2), получим значение электродвижущей силы самоиндукции εs:
. (5)
Физический смысл коэффициента самоиндукции вытекает из формулы (5). Коэффициент самоиндукции
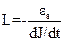(6)
числено равен той электродвижущей силе самоиндукции, которая возникает при изменении силы тока в замкнутом контуре на один ампер за одну секунду.
|
|
За единицу коэффициента самоиндукции в СИ принимается генри (Гн):
[Гн] = 
Величина коэффициента самоиндукции зависит от геометрической формы и размера проводника; для катушки (соленоида) коэффициент самоиндукции в очень большой степени зависит от числа витков и магнитной проницаемости сердечника и выражается формулой:
L = μ0 μn2V,
где n – число витков катушки, приходящееся на единицу её длины
μ – магнитная проницаемость сердечника,
V – объём катушки,
μ0 – магнитная постоянная, μ0 = 4π·10-7Гн/м
Знак минус в формуле (5) означает, что εs имеет всегда такое направление в контуре, которое препятствует изменению тока, вызывающему эту электродвижущую силу. Чем больше изменение тока, тем больше возникает εs, а значит и сопротивление такому изменению. εs аналогична инерции в механике. В результате в цепи возникает как бы добавочное сопротивление переменному току. Оно получило название индуктивного сопротивления Ri. Его величина вычисляется по формуле
Ri =ωL, (7)
где ω – круговая или циклическая частота колебаний тока в контуре.
По определению
(8)
где Т и ν – период и частота (число колебаний в единицу времени) переменного тока.
Представим себе электрическую цепь, состоящую из генератора переменного тока с электродвижущей силой ε, ключа К, катушки с индуктивностью L и омическим сопротивлением R0 (рис. 3). Под омическим понимают сопротивление, которое возникает вследствие столкновений упорядочено движущихся электронов с узлами кристаллической решетки. Оно зависит от физических свойств проводника и не обладает индуктивностью.
|
|
Рис.3
Омическое сопротивление вычисляют по формуле:
Rо= ρ 
, (9)
где ℓ - длина проводника, Ѕ – площадь сечения, ρ – удельное сопротивление, характеризующее материал проводника (табличное значение).
Если замкнуть ключ К, то по цепи потечет переменный ток J, а в катушке возникает электродвижущая сила самоиндукции (5). Применим к этой замкнутой цепи второе правило Кирхгофа:
. (10)
Пусть электродвижущая сила генератора изменяется по гармоническому закону:
ε = εо sίn ωt, (11)
где ε0 – его максимальное (амплитудное) значение. Выражая из (10) силу тока J, получим:
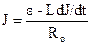, (12)
Таким образом, сила тока в цепи (12) не обращается в ноль, когда ε становится равным нулю. Сила тока изменяется с некоторым запозданием по сравнению с ε (11). Анализ показывает, что закон изменения силы тока можно выразить следующей формулой:
J=Jо sίn (ωt –φ), (13)
где J0 – максимальное (амплитудное) значение силы тока,
φ – фаза, на которую запаздывает изменение тока в цепи от изменения ε
(сдвиг фазы).
Выразим амплитуду и сдвиг фазы установившегося в цепи тока от заданных значений ε0,R0,L и ω. Для этого найдем производную от тока (13) по времени t:
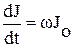соs(ωt-φ). (14)
Подставляя в формулу (10) выражения электродвижущей силы генератора (11), силы тока в цепи (13) и изменение этой силы тока в цепи (13) и изменение этой силы (14), получим:
JоRо sίn (ωt-φ) = εо sίn ωt - LωЈо соs (ωt-φ) (15)
или L ωJо соs (ωt-φ) + JоRо sίn (ωt-φ) -εо sίn ωt = 0.
Применяя правила тригонометрии, представим (15) в развернутом виде:
L ωJо соs ωt · соsφ +L ωJоsίn ωt·sίnφ +JоRоsίnωt·соsφ-JоRо соs ωt· sίnφ-εоsίnωt=0.
Сгруппируем члены отдельно с соs ωt и отдельно с sίn ωt:
(LωJо соsφ- ЈоRоsίn φ) соs ωt+(LωJоsίn φ+ LωJо соsφ-εо)sίnωt=0. (16)
Для любого момента времени соs ωt 0 и sίnωt 0. Поэтому уравнение (16) может быть выполнено только при условии, если оба выражения в скобках одновременно равны нулю:
LωJо соsφ- ЈоRоsίn φ =0
LωJоsίn φ+ЈоRо соsφ- εо =0
или
LωJо соsφ - ЈоRоsίn φ =0
LωJоsίn φ + ЈоRо соsφ = εо. (17)
Возводя оба равенства (17) в квадрат и почленно их складывая, получим:
(ωL)2J 
+ 
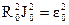. (18)
Из (18) выразим искомое значение Јо ;
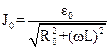. (19)
Сопоставляя равенство (19) с законом Ома, заметим, что знаменатель
. (20)
совпадает с общим сопротивлением всей цепи и, включающей омическое сопротивление Ro и индуктивное ωL сопротивления. Из формулы (20) путем возведения её в квадрат, легко выразить индуктивность катушки L. С учетом связи между ω и ν (8), значение индуктивности равно:
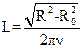. (21)
Для нахождения величины сдвига фаз φ между J и ε можно воспользоваться одним из равенств (17), например, верхним:
LωJо соsφ = ЈоRоsίn φ. (22)
Разделив правую и левую части (22) на Јо соsφ получаем:
Lω = Rо tg φ.
Отсюда находим искомое φ:
tg φ = 
. (23)
Зная амплитудное значение тока (19) и сдвиг фазы φ (23), путем подстановки их в закон изменения силы тока (13) можно найти протекающий в цепи ток в любой момент времени.
На практике при вычислении амплитудных значений падений напряжений, токов, сопротивлений и сдвига фаз часто применяют так называемый метод векторных диаграмм. Он заключается в том, что каждый колебательный процесс отождествляют с вращением некоего вектора в плоскости вокруг точки, совпадающей с его началом, против часовой стрелки. Длина этого вектора принимается равной амплитуде колебания, а скорость вращения совпадает с ω. Очевидно, что если некоторая совокупность колебаний происходит с одинаковой частотой, то соответствующие им вращающиеся вектора, совмещенные своими началами, будут неподвижны относительно друг друга. Причем угловые расстояния между векторами как раз равняются сдвигам фаз между колебаниями. Такая застывшая картина фиксированных векторов относительно некоторой оси отсчета Х, проходящей через начальную точку и совпадающей по направлению, например, с одним из них, называется векторной диаграммой данной совокупности колебаний. Параметры результирующего колебания (амплитуду и фазу) находят путем векторного сложения этих указанным образом ориентированных векторов.
В качестве примера применим метод векторных диаграмм для вычисления характеристик колебаний ε и J в цепи, соответствующей схеме на рис. 3. Пусть ось отсчета Х совпадает с направлением вектора тока J0 (рис. 4).
Рис.4
Тогда амплитуду падения напряжения на омическом сопротивлении R0 будет R0J0. Сдвиг фаз между вектором R0J0 и осью Х равняется нулю. Поэтому вектор R0J0 совпадает по направления с вектором J0. Амплитуда падения напряжения на индуктивном сопротивлении ωL будет ωLJ0. Однако, как было показано выше, ток в катушке всегда отстает по фазе с прилагаемой ε. Чтобы оценить величину этого отставания, положим в формуле (23) R0 = 0. Тогда tgφ = ∞, а φ = 
. Таким образом, колебание, соответствующее падению напряжения на индуктивности, опережает падение напряжения на омическом сопротивлении R0J0 на 90о.
Для нахождения результирующего падения напряжения на катушке Z сложим вектора R0J0 и ωLJ0. По теореме Пифагора получаем:
Z 2 = (R0J0)2 + (ωLJ0)2 . (24)
Так как при последовательном соединении ток в цепи везде одинаков, результирующее падение напряжения на катушке можно представить в виде произведения Z= R J0, где R – общее сопротивление цепи. Тогда, сокращая (24) на J2, имеем:
R2 = 
+ (ωL)2
или
что полностью совпадает с формулой (20).
Очевидно, результирующее падение напряжения на катушке равно электродвижущей силе ε, приложенной к этой катушке. Для нахождения сдвига фаз φ между ε и Jрассмотрим треугольник ОМN. Из определения тангенса угла φ имеем:
что также совпадает с вышевыведенной формулой (23).
3. Экспериментальная часть.
ОПИСАНИЕ УСТАНОВКИ
Для определения коэффициента самоиндукции и угла сдвига фаз необходимо иметь катушку индуктивности L с сердечником и ярмом, источник переменного и постоянного тока ИТ, вольтметр V и амперметр А, предназначенных для измерения постоянных и переменных напряжений и токов, и ключ К для замыкания и размыкания цепи. Для производства работы собирают электрическую цепь по схеме (рис.5):
Рис.5
ВЫПОЛНЕНИЕ РАБОТЫ
1. Собрать электрическую цепь (рис. 5) с источником переменного тока. Для этого провода, подходящие к ИТ, присоединяют к клеммам переменного напряжения.
Опыт производят для трех случаев:
а) в цепь включают катушке индуктивности без сердечника и ярма. Напряжение ε1 (около 10В) подается путем вращения ручки регулировки ИТ. Регистрируют силу тока J1. Шкалу амперметра выбирают до 1 А;
б) в цепь включают катушку индуктивности с сердечником, но без ярма. Напряжение ε2 оставляют также около 10 В. Регистрируют силу тока Ј2. Шкалу амперметра выбирают до 0,25 А;
в) в цепь включают катушку индуктивности с сердечником и ярмом. Напряжение ε3 и шкалу амперметра оставляют теми же что и в предыдущем случае Б. Регистрируют силу тока Ј3.
2. По закону Ома для каждого из трех указанных в пункте 1 случаев определить величину полного сопротивления катушки R1, R2, R3:
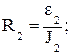
(25)
3. Собрать электрическую цепь (рис. 5) с источником постоянного тока. Для этого провода, подходящие к ИТ, присоединяют к клеммам постоянного напряжения. Также как и для переменного тока. Опыт проводят для трех случаев:
а) катушка без сердечника и ярма,
б) катушка с сердечником, но без ярма,
в) катушка с сердечником и ярмом.
Для каждого из трёх случаев регистрируют силу тока (
) при ранее выбранном и установленном на ИТ напряжении (
) Напряжения выбирают в интервале от 5 до 15 В. Шкала амперметра во всех случаях остается одной и той же до 1 А.
4. По закону Ома для каждого случая указанного в пункте 3 вычислить величину омического сопротивления катушки R01,R02, и R03:
(26)
5. С помощью формулы (21) найти величину L катушки для каждого из трёх случаев:
а) катушка без сердечника и ярма (L1),
б) катушка с сердечником, но без ярма (L2),
в) катушка с сердечником и ярмом (L3),
Частота тока городской сети ν = 50 с-1=50 Гц.
6. С помощью формулы (23) с учетом определения (8) вычислить величину сдвига фаз между током и напряжением для каждого из трех случаев:
а) катушка без сердечника и ярма (φ1),
б) катушка с сердечником, но без ярма (φ2),
в) катушка с сердечником и ярмом (φ3).
7. Все величины записать в таблицы.
Таблица 1
Переменный ток
| ε1 | J1 | R1 | ε2 | J2 | R2 | ε3 | J3 | R3 |
Таблица 2
Постоянный ток
| 
| 
| 
| 
| 
| 
| 
| 
|
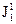
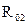
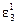
Таблица 3
Коэффициент самоиндукции и угол сдвига фаз
| L1 | L2 | L3 | φ1 | φ2 | φ3 |
8. По результатам измерений выявить закономерности изменений полного R и омического R0 сопротивлением катушки, коэффициента ее самоиндукции L и угла сдвига фаз φ между током и напряжением при переходе от одного случая к другому. Сделать вывод о причинах таких изменений. Результаты записать в тетради.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Взаимосвязь электрических и магнитных явлений. Электромагнитная индукция. ЭДС индукции.
2. Явление самоиндукции. ЭДС самоиндукции. Индуктивность и её физический смысл.
3. Принцип работы генератора переменного тока.
4. Цепи переменного тока с активным, емкостным и индуктивным сопротивлениями. Полное сопротивление цепи переменного тока. Обобщенный закон Ома.
5. Физическая причина сдвига фаз между током и напряжением в цепи переменного тока.
6. Энергия магнитного поля. Объемная плотность энергии магнитного поля.
Работа № 6