Определители квадратных матриц

Основные сведения о матрицах

Матрицейразмера 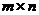называется прямоугольная таблица чисел, содержащая т строк и п столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Для обозначения матриц используются прописные латинские буквы, например, А, В, С,..., а для обозначения их элементов - соответствующие строчные буквы с двойной индексацией: , где i - номер строки, j - номер столбца.

Общий вид матрицы размерности 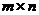следующий:

(1)

или, в сокращенной записи, ; ;

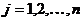
Например,

.

Наряду с круглыми скобками используются и другие обозначения матрицы: , .

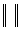Две матрицы A и В одинаковой размерности называются равными, если они совпадают поэлементно, т.е. для любых ;

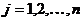
Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой,а из одного столбца - матрицей (вектором)-столбцом: - матрица-строка;

.

Определение. Матрица называется квадратной n -го порядка (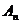), если число ее строк равно числу столбцов и равно п.

Элементы матрицы , у которых номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы , , …, .

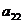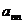Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Если у диагональной матрицы n -го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n -го порядка, она обозначается .

Матрица любого размера называется нулевой, если все ее элементы равны нулю:

Операции над матрицами

1. Умножение матрицы на число.

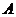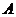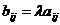Произведением матрицы на число называется матрица , каждый элемент которой равен произведению соответствующего элемента матрицы на число , т.е. для ; .

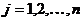Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.

В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е .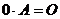

2. Сложение матриц.

Суммой двух матриц 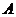и одинакового размера 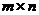называется матрица 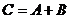, каждый элемент которой 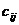равен сумме соответствующих элементов матриц 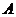и , т.е. для ; 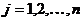(т.е. матрицы складываются поэлементно).

3. Вычитание матриц.

Разность двух матриц одинакового размера определяется через предыдущие операции: .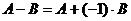

Умножение матриц.

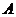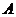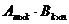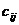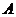Произведение матриц и определено, когда число столбцов матрицы равно числу матрицы . Произведением матриц называетсятакая матрица , каждый элемент которой равен суммепроизведений элементов -й строки матрицы на соответствующие элементы 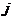-го столбца матрицы : , ; .

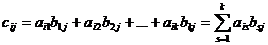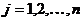(Иными словами, матрицы умножаются строка на столбец).

Операции над матрицами обладают следующими свойствами:

1) ;

2) ;

3) .

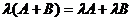4) ;

5) ;

6) ;

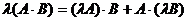7) .

Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:

а) Если произведение матриц существует, то после перестановки сомножителей местами произведения матриц 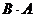может и не существовать.

б) Если даже произведения и 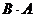существуют, то они могут быть матрицами разных размеров.

в) В случае, когда оба произведения и 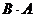существуют и оба - матрицы одинакового размера (это возможно только при умножении квадратных матриц 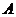и одного порядка), коммутативный (переместительный) закон умножения, вообще говоря, не выполняется, т.е. .

В частном случае коммутативным законом обладает произведение любой квадратной матрицы 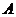-го порядка на единичную матрицу 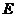того же порядка, причем это произведение равно :

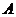Таким образом, единичная матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.

г) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из того, что , не следует, что или .

5. Возведение в степень. Целой положительной степенью квадратной матрицы 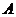называется произведение матриц, равных 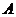, т.е.

.

Заметим, что операция возведения в степень определена только для квадратных матриц. Полагают , . Нетрудно показать, что , . Если , то это не означает, что матрица .

6. Транспонирование матрицы - переход от матрицы 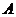к матрице , в которой строки и столбцы поменяны местами с сохранением порядка. Матрица называется транспонированной относительно матрицы :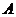

, . (2)

Из определения следует, что если матрица 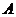имеет размер 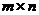, то транспонированная матрица имеет размер .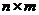

Свойства операции транспонирования:

1)

2)

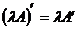
3)

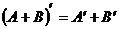
4) .

Определители квадратных матриц

Определитель квадратной матрицы – это число, характеризующего эту матрицу. Он обозначается или .

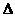Определителем матрицы первого порядка 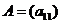, или определителем первого порядка, называется число, определяемое по формуле: .

Например, пусть , тогда .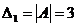

Определителем матрицы второго порядка 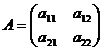, или определителем второго порядка, называется число, которое вычисляется по формуле:

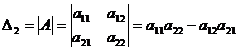(3).

Произведения 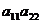и 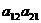называются членами определителя второго порядка.

Пусть дана квадратная матрица третьего порядка:

.

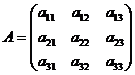Определителем матрицы 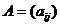третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

(4).

Это число представляет алгебраическую сумму, состоящую из 6 слагаемых, или 6 членов определителя. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Знаки, с которыми члены определителя входят в формулу (4), легко запомнить, пользуясь схемой (рис. 1), которая называется правилом Сарруса.

Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия.

Рассмотрим квадратную матрицу n-го порядка:

.

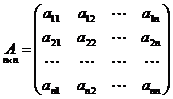Из общего числа элементов этой матрицы выберем набор, содержащий n элементов, таким образом, чтобы в него входило по одному элементу из каждой строки и каждого столбца. Например, наборы элементов 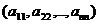или 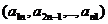соответствуют главной и побочной диагоналям матрицы.

Любой такой набор можно упорядочить, записав сначала элемент из 1-й строки, затем из 2-й и т.д., т.е.

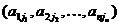. (5)

Номера столбцов 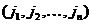образуют при этом перестановку J из n чисел: 1, 2,..., n. Всего существует различных перестановок из n.

Введем понятие беспорядка, или инверсии, в перестановке J. Это наличие пары чисел, в которой большее число предшествует меньшему. Например, в перестановке из трех чисел J =(2; 1; 3) имеется одна инверсия (2; 1), а в перестановке J =(3; 2; 1) - три: (3; 2), (3; 1), (2; 1). Обозначим через r(J) количество инверсий в перестановке J.

Возвращаясь к наборам (5) из элементов матрицы А, мы можем каждому такому набору поставить в соответствие произведение его элементов:

. (6)

и число r(J), равное количеству инверсий в перестановке из номеров соответствующих столбцов.

Определителемквадратной матрицы п-го порядка, или определителем п-го порядка, называется число, равное алгебраической сумме членов, каждый из которых является произведением п элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как где r(J) - число инверсий в перестановке J из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания:

(7)

где сумма берется по всем перестановкам J.

Заметим, что с ростом n резко увеличивается число членов определителя (), поэтому даже для n = 4 использование формулы (7) весьма трудоемко (получим 24 слагаемых).

На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.

Пусть дана квадратная матрица А n -го порядка.

Минором элемента матрицы n -го порядка называется определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i -й строки и j- гo столбца.

Каждая матрица n -го порядка имеет миноров (n-1)-го порядка. Алгебраическим дополнением 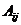элемента матрицы n -го порядка называется его минор, взятый со знаком :

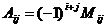, (8)

т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (i+j) - четное число, и отличается от минора знаком, когда (i+j) - нечетное число.

Для вычисления определителей квадратных матриц удобно пользоваться следующей теоремой:

Теорема Лапласа (частный случай). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

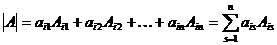(9)

(разложение по элементам i -й строки; i = 1,2,… n;

(10)

(разложение по элементам j -го столбца; j =1,2,..., n).

 

Таким образом, применение теоремы Лапласа позволяет свести вычисление определителей n- гопорядка к вычислению более простых определителей (n- 1)-го порядка.

Свойства определителей

1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.

2. Если все элементы какой-либо строки (столбца) матрицы умножить на число , то ее определитель умножится на это число .

Замечание. За знак определителя можно выносить общий множитель элементов любой строки или столбца в отличие от матрицы, за знак которой можно выносить общий множитель лишь всех ее элементов.

3. При транспонировании матрицы ее определитель не изменявется: .

4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

5. Если квадратная матрица содержит две одинаковые строки {столбца), то ее определитель равен 0.

6. Если элементы двух строк {столбцов) матрицы пропорциональны, то ее определитель равен 0.

6. Сумма произведений элементов какой-либо строки {столбца) матрицы на алгебраические дополнения элементов другой строки{столбца) этой матрицы равна 0, т.е.

при . (11)

Замечание. Объединяя результат теоремы Лапласа и свойство 7, получаем:

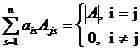. (12)

7. Определитель матрицы не изменится, если к элементам какой-либо строки {столбца) матрицы прибавить элементы другой строки {столбца), предварительно умноженные на одно и то же число.

9. Сумма произведений произвольных чисел 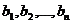на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа .

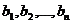10. Определитель произведения двух квадратных матриц равен произведению их определителей: 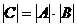, где ; А и В - матрицы п-го порядка.

Замечание. Из свойства 10 следует, что даже если 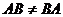, то .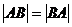

Перечисленные свойства определителей позволяют существенно упростить их вычисление, особенно для определителей высоких порядков. При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств 1-9, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).

Обратная матрица

Матрица 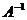называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:

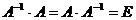(13)

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.

Для существования матрицы 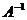таким условием является требование .

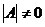Если определитель матрицы отличен от нуля (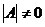), то такая квадратная матрица называется невырожденной, или неособенной; в противном случае (при ) - вырожденной, или особенной.

Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрица 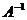существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.

Пусть 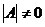. Рассмотрим квадратную матрицу n -го порядка , называемую присоединенной, элементы которой являются алгебраическими дополнениями элементов матрицы А^T, транспонированной к А: , , .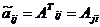

Тогда обратную матрицу определяют как

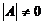(), (14)

Алгоритм вычисления обратной матрицы:

1. Находим определитель исходной матрицы. Если , то матрица А - вырожденная и обратной матрицы 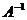не существует. Если 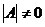, то матрица А - невырожденная и обратная матрица существует.

2. Находим матрицу , транспонированную к А.

3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу : (; ).

4. Вычисляем обратную матрицу по формуле (1.14).

Для невырожденных матриц выполняются следующие свойства:

1.

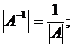
2.

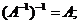
3.

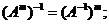
4.

5. .

Ранг матрицы

В матрице А размера 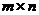вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k -го порядка, где . Определители таких подматриц называются минорами k-го порядка матрицы А.

Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

Ранг матрицы А обозначается rang А, или r(А).

Из определения следует:

а) ранг матрицы не превосходит меньшего из ее размеров, т.е. ;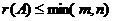

б) тогда и только тогда, когда все элементы матрицы равны нулю, т.е. ;

в) для квадратной матрицы n -го порядка тогда и только тогда, когда матрица невырожденная.

В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются преобразования, сохраняющие ранг матрицы.

Назовем элементарными преобразованиями матрицы следующие:

1) Отбрасывание нулевой строки (столбца).

2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.

3) Изменение порядка строк (столбцов) матрицы.

4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5) Транспонирование матрицы.

Теорема. Ранг матрицы не изменяется при ее элементарных преобразованиях.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.

Матрица А называется ступенчатой, если она имеет вид:

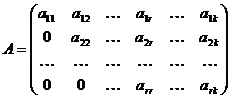, (15)

где , ; .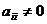

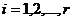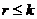Замечание. Условие 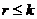всегда может быть достигнуто транспонированием матрицы.

Очевидно, что ранг ступенчатой матрицы равен r так как имеется минор r- гопорядка, не равный нулю:

,

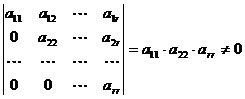Для рангов матриц справедливы следующие соотношения:

1) ;

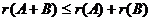2) ;

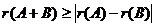3) ;

4) ;

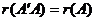5) , если В - квадратная матрица и ;

6) 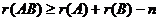,где п - число столбцов матрицы А или строк матрицы В.

В матрице А обозначим ее строки следующим образом:

; , … .

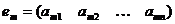Две строки матрицы называются равными, если равны их соответствующие элементы:

, если , .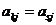

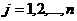Арифметические операции над строками матрицы (умножение строки на число, сложение строк) вводятся как операции, проводимые поэлементно:

;

.

Строка е называется линейной комбинацией строк матрицы, если она равна сумме произведений этих строк на произвольные действительные числа:

, (16)

где - любые числа.

Строки матрицы 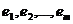называются линейно зависимыми, если существуют такие числа 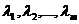, не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:

, (17)

где .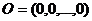

Линейная зависимость строк матрицы означает, что хотя бы дна строка матрицы является линейной комбинацией остальных.

Если линейная комбинация строк (17) равна нулю тогда и только тогда, когда все коэффициенты 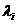равны нулю, т.е. 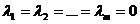, то строки 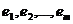называются линейно независимыми.

Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки {столбцы). Их называют базисными.

Теорема о ранге матрицы играет принципиальную роль в матричном анализе, в частности при исследовании систем линейных уравнений.