ИСТЕЧЕНИЕ С УЧЕТОМ СОПРОТИВЛЕНИЙ

ТГС с ОТ

 

Методические указания для контрольныхработ.

 

 

для студентов строительного института

 

 

Брянск 2014

 

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИИ

Брянская государственная инженерно-технологическая академия

 

 

Кафедра энергетики и автоматизации производственных процессов

 

 

Утверждена научно-методическим

советом БГИТА

Протокол______от________2014 г.

 

 

ТТГ с ОТ

 

 

Методические указания для

Контрольных, самостоятельных и практических

Работ.

 

 

для студентов строительного института

 

 

Брянск 2014

 

Составитель: Горюнова Е.А. – доцент кафедры энергетики и автоматизации

производственных процессов Брянской государственной

инженерно-технологической академии

 

Указания включают техническое и методическое обеспечение, содержание работы.

Устанавливают методику и порядок выполнения,требования к выполнению и оформлению.

 

Рецензент: Ульянов А.А. – доцент кафедры ЭиАПП Брянской государственной

инженерно-технологической академии

 

 

Рекомендовано учебно-методической комиссией СИ

Протокол №_____от ________2014г.

 

 

Содержание

 

1 Введение…………………………………………………………………………..

2 Содержание контрольной работы……………………………..

2.1Расчет газовой смеси……………………………………..…………….....

2.1.1Теоретические сведения……………………………………………..

2.1.2Условия задачи…………………………………………………………

2.1.3Пример решения задачи…………………………………………………

2.2 Истечение через сопло……..…………………………………….…………...

2.2.1Теоретические сведения………………………………………………

2.2.2Условия задачи…………………………………………………………

2.2.3Пример решения задачи……………………………………………….

2.3 Расчет компрессора. ……………………………...…………………………..

2.3.1Теоретические сведения………………………………………………...

2.3.2Условия задачи…………………………………………………………

2.3.3Пример решения задачи……………………………………………….

2.4Расчет теплопроводности через многослойную плоскую

стенку………………………………………………………………...………

2.4.1Теоретические сведения……………………………………………..

2.4.2Условия задачи…………………………………………………………

2.4.3Пример решения задачи……………………………………………….

Рекомендуемая литература……………………………………………

 

ВВЕДЕНИЕ

 

ТГС с ОТ – наука, которая изучает методы получения, преобразования, передачи и использования теплоты, а также принципы действия и конструктивные особенности тепловых машин, аппаратов и устройств. Теплота используется во всех областях деятельности человека. Для установления наиболее рациональных способов его использования, анализа экономичности рабочих процессов тепловых установок и создания новых, наиболее совершенных типов тепловых агрегатов необходима разработка теоретических основ теплотехники.

Целью данной работы является закрепление теоретических знаний и получение навыков в самостоятельном решении задач, связанных с различными теплотехническими расчетами, такими как:

- газовой смеси;

- параметров истечения через сопло;

- компрессора;

- теплопроводности через многослойную плоскую стенку.

Решение задач должно сопровождаться кратким поясняющим текстом. Все данные, необходимые для выполнения задания, но не приведенные в исходных данных, принимаются самостоятельно по рекомендованной учебной или справочной литературе, при этом на соответствующий литературный источник делается ссылка. Список используемых источников приводится в конце работы.

Вычисление всех величин должно даваться в развернутом виде: сначала приводится формула в общем виде, затем подставляются численные значения параметров, в нее входящих и вычисляются результаты.Обозначение всех величин и их размерности должны отвечать требованиям системы СИ.

 

 

2.1 Расчет газовых смесей

2.1.1 Теоретические сведения

Состав газовой смеси определяется количеством каж­дого из газов, входящих в смесь, и может быть задан мас­совыми или объемными долями.

Массовая доля определяется отношением массы отдель­ного газа, входящего в смесь, к массе всей смеси:

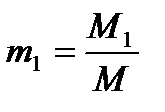; ; ; ……, ;(2.1.1) где M₁, M₂, M_{3, …..,}M_n — массы отдельных газов и М — масса всей смеси.

Объемной долей газа называют отношение объема каждого компонента, входящего в смесь, к объему всей газовой смеси при условии, что объем каждого компонента отнесен к давлению и температуре смеси (приведенный объем):

; ; ; · · ·, ; (2.1.2)

где V₁, V₂, V_{3, …..,}V_n - приведенные объемы компонентов газов, входящих в смесь;V - общий объем газовой смеси.

Очевидно, что M₁ + M₂ + M₃ + · · · + M_n=M; m₁ + m₂ +m₃ + · · · + m_n = 1,(2.1.3)

а также V₁ + V₂ + V₃ +· · · + V_n = V; r₁ + r₂ + r₃ + · · · + r_n = 1(2.1.4)

 

Для перевода массовых долей в объемные пользуются формулой

(2.1.5)

Перевод объемных долей в массовые производится по формуле

(2.1.6)

Плотность смеси определяется из выражения

ρ_см = ∑ r_i·ρ_i кг/м³ (2.1.7)

и, если известен массовый состав, по формуле

(2.1.8)

Удельный объем смеси представляет величину, обратную ρ_см; поэтому, если дан объемный состав смеси, то

(2.1.9)

Если же известен массовый состав, то

(2.1.10)

Из уравнения (2.7) легко получается значение так называемой кажущейся молекулярной массы газовой смеси

(2.1.11)

и через массовый состав

(2.1.12)

Газовую постоянную смеси газов R_см,Дж/(кг·град) можно выра­зить либо через газовые постоянные отдельных компонен­тов, входящих в смесь, либо через кажущуюся молеку­лярную массу смеси

или 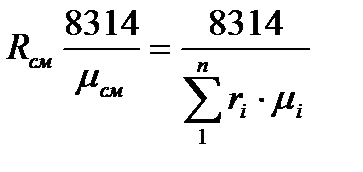(2.1.13,14)

Связь между давлением газовой смеси и парциальными давлениями отдельных компонентов, входящих в смесь, устанавливается следующей зависимостью (закон Даль­тона), легко получаемой из основного уравнения кинети­ческой теории газов:

р = р₁ + р₂ + р₃ · · · + р_n(2.1.15)

где р — общее давление газовой смеси;

р₁, р₂, р₃ · · · р_n - парциальные давления отдельных компонентов, входящих в смесь.

Парциальные давления определяются проще всего, если известны объемные доли отдельных компонентов, входящих в смесь: р₁ = pr₁, p₂ = pr₂ и т.д. или вообще р_i= pr_i— парциальное давление любого газа, входящего в смесь. Если известны массовые доли, то парциальное давление любого газа, входящего в смесь, определяется из фор­мулы

(2.1.16)

 

2.1.2 Условия задачи №1

Задан состав газовой смеси в массовых (объемах) долях. Произвести пересчет газовой смеси, вычислить молекулярную массу смеси, газовую постоянную смеси, а так же парциальное давление и плотность каждого из компонентов при условии, что газовая смесь находится при нормальных физических условиях. Определить средние массовые теплоемкости газовой смеси в диапазоне температур t₁ и t₂ при постоянном объеме и при постоянном давлении (р_атм=760мм рт.ст.)

№	Н2	СО	СО2	N2	t1	t2
	0.51	0.24	0.06	0.19
	0.52	0.06	0.24	0.18
	0.20	0.22	0.04	0.54
	0.54	0.04	0.28	0.14
	0.14	0.28	0.04	0.54
	0.25	0.05	0.40	0.30
	0.30	0.10	0.15	0.45
	0.45	0.15	0.1	0.3
	0.122	0.071	0.004	0.803
	0.803	0.004	0.071	0.122
	0.120	0.073	0.002	0.805
	0.805	0.002	0.120	0.073
	0.002	0.805	0.073	0.12
	0.50	0.10	0.22	0.18
	0.18	0.22	0.50	0.10
	0.06	0.24	0.52	0.18
	0.36	0.34	0.18	0.12
	0.18	0.12	0.36	0.34
	0.11	0.09	0.25	0.55
	0.55	0.25	0.09	0.11
	0.46	0.32	0.15	0.07
	0.15	0.07	0.46	0.32
	0.07	0.15	0.32	0.46
	0.34	0.18	0.12	0.36
	0.08	0.14	0.47	0.31
	0.12	0.13	0.23	0.52

 

 

2.1.3 Пример расчета задачи

Дано:

m_H2=0.20; m_co2=0.04; m_co=0.22; m_N2=0.54; t₁=70^oC; t₂=1050^oC;

Найти:

R_Н2=?; r_CO=?; r_CO2=?; r_N2=?; μ_cm=?; R_cm=?; p_H2=?; p_CO=?; p_CO2=?; p_N2=?; ρ_cm=?; с_Vcm=?; с_ρcm=?

Решение:

Перевод массовых долей в объемные осуществляется по формуле:

Где r_i–объемная доля компонента

m_i –массовая доля компонента

μ_i– кажущаяся молекулярная масса компонента

Аналогично

 

Проверка

Газовая постоянная смеси

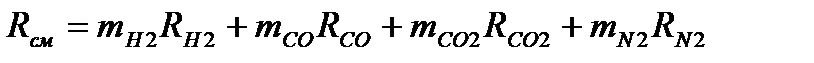
(Значения R_H2, R_CO, R_CO2, R_N2 –из справочника Рабиновича- т.IIIcтp. 327)

Кажущаяся молекулярная масса смеси:

(Из справочника μ_H2=2.016, μ_CO=28.01, μ_CO2=44.01, μ_N2=28.026)

 

Проверка

Парциальные давления:

р-общее давление газовой смеси

Плотность

где ρ_i–плотность каждого из компонентов

(Рабинович- ρ_H2=0.090 кг/м³ ρ_CO=1.250 кг/м³ ρ_CO2=1.977 кг/м³ ρ_N2=1.251 кг/м³)

Средняя массовая теплоемкость газовой смеси

 

Где С_pi, C_vi – средняя массовая теплоемкость компонента при постоянном давлении, объеме, кДж/кг*град

При t=70⁰С (по т. 5, стр 45)C_vi:

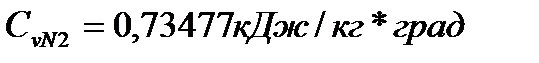
С_pi:

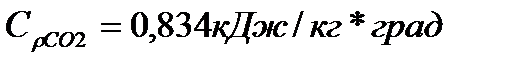
При t₂=1050⁰С

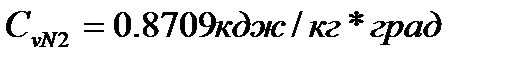
70⁰С

1050⁰С

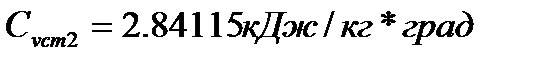
Средняя массовая теплоемкость газовой смеси в диапазоне температур от 70⁰С до 1050⁰С:

-при постоянном объеме

-при постоянном давлении

Ответ:

 

r_H2 = 0,781; r_CO = 0,061; r_CO2 = 0,007; r_N2 = 0,151.

 

 

 

 

 

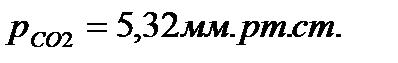
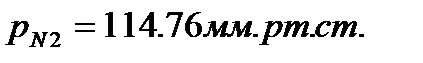
Истечение через сопло

Теоретические сведения

При решении задач, связанных с истечением газа через сопла (насадки) (рисунок2.2.1), чаще всего приходится опреде­лять скорость истечения и расход, т. е. количество газа, вытекающего в единицу вре­мени. В этих случаях необ­ходимо прежде всего найти отношение , где р₂ —давление среды на выходе из сопла; р₁ —давление среды на входе в сопло.

Рисунок 2.2.1 – Истечение газа

Полученное числовое значение сравнивают с так называемым критическим отношением

давлений для дан­ного газа, определяемым из равенства и равным:

= (2.2.1)

 

для одноатомных газов при k = 1,67

(2.2.2)

для двухатомных газов при k = 1,4

(2.2.3)

для трех- и многоатомных газов при k = 1,29

(2.2.4)

Если адиабатное истечение газа происходит при > то теоретическая скорость газа у устья суживающегосясопла определяется по формуле:

, (2.2.5)

где k — показатель адиабаты; v₁ — удельный объем газа на входе в сопло.

Заменяя для идеального газа в формуле (2) p₁v₁ на RT₁, получаем

, (2.2.6)

 

В формулах (2.2.5) и (2.2.6) значенияp, v и R даны соответственно в следующих единицах: н/м², кг/м³и дж/ (кг∙град)

Теоретическая скорость газа может быть также най­дена по формуле

^, (2.2.7)

где i₁ иi₂ соответственно энтальпии газа в начальном и конечном состояниях в дж/кг.

Расход газа определяется по формуле

(2.2.8)

где f — выходное сечение сопла в м².

Если же адиабатное истечение газа происходит при ≤ , то теоретическая скорость газа в устье суживающегося сопла будет равна критической скорости и определится по уравнению

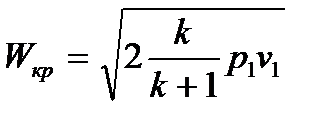(2.2.9)

Критическая скорость по формуле (2.2.9) зависит только от начального состояния газа и показателя адиабаты k. Поэтому, подставляя значение k для различных рабочих тел, получим более удобные формулы для определения критической скорости. В частности, для двухатомных газов

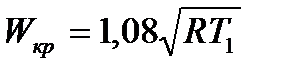(2.2.10) или (2.2.11)

 

Расход газа в этом случае будет максимальным и может быть вычислен по уравнению

(2.2.13)

Подставляя в эту формулу значение k, получаем для двухатомных газов

(2.2.14)

для трехатомных газов

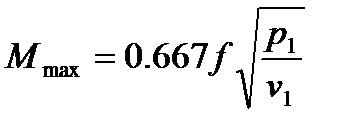(2.2.15)

Во всех перечисленных формулах следует брать р в н/м², av — в м³/кг. Расход газа получается в кг/сек.

Для получения скоростей истечения выше критиче­ских (сверхзвуковые скорости) применяется расширя­ющееся сопло, или сопло Лаваля (рисунок 2.2.2). В минималь­ном сечении сопла Лаваля скорость движения газа равна критической скорости или скорости звука, определяемой параметрами р_кр и v_Kp.

Площадь минималь­ного сечения сопла опре­деляется по формуле

(2.2.16)

Рис. 2.2.2 – Сопло Лаваля

 

Площадь выходного сечения сопла

(2.2.17)

причем — удельный объем газа при давлении среды р₂

Длина расширяющейся части сопла определяется по уравнению

(2.2.18)

где d и d _min— соответственно диаметры выходного и минимального сечений;

α — угол конусности расширяющейся части сопла.

При истечении водяного пара все общие законы, установленные для истечения газов, остаются в силе.Однако формулы истечения для газов, в которые входит величина k> для водяного пара будут приближенными, так как значение k для пара в процессе изменения его состояния непостоянно.

ИСТЕЧЕНИЕ С УЧЕТОМ СОПРОТИВЛЕНИЙ

Действительная скорость истечения всегда меньше теоретической, так как процесс истечения связан с нали­чием трения. Если обозначить действительную скорость истечения через W_дто потеря кинетической энергии струи

 

откуда

(2.2.19)

Обозначая 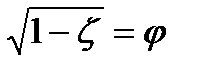(2.2.20)

Получаем

W_д = W^′ = φ∙W (2.2.21)

Коэффициент φ называют скоростным коэффициентом сопла, а коэффициент ζ = 1 – φ² – коэффициентом потери энергии в сопле.

Часть кинетической энергии в результате трения пре­вращается в тепло, которое при отсутствии теплообмена повышает энтальпию и энтропию рабочего тела, вытека­ющего из сопла. Поэтому состояние газа или пара в конце действительного процесса истечения в диаграмме is изо­бражается точкой, всегда расположенной правее точки, характеризующей конечное состояние рабочего тела в идеальном процессе истечения.

Пользуясь диаграммой is, можно определить пара­метры в конце процесса расширения.

Если дана началь­ная точка А (рисунок 3) и коэффициент ζ (или φ), то, проводя адиабату АВ, откладывают от точки В вверх отрезок ВС = i ₂ — i_2d и, проведя через точку С горизонталь до пере­сечения с конечной изобарой р₂, получают точку D, характеризующую состояние рабочего тела в конце дей­ствительного процесса истечения. По ней можно найти необходимые параметры пара: удельный объем, степень сухости и т. д.

 

Рисунок2.2.3

Если же даны начальное и конечное состояния, т. е. точки А и D, то очень легко изобразить потери работы в виде отрезков, проведя через точку D горизонталь до пересечения ее с адиабатой. Отношение отрезков даст значение коэффициента потери энергии, а следовательно, и скоростного коэффициента.

 

 

Условия задачи №2

 

Воздух из резервуара с постоянным давлением Р₁ и температурой t₁ вытекает через сопло в среду с давлением Р₂. Определить скорость потока на выходе из сопла, критические параметры потока, критическую скорость истечения, расход газовой смеси. Площадь сопла – F_MIN. Нарисовать профиль сопла, указав в характерных сечениях численные значения основных параметров потока (температура, удельный объем, давление, скорость). Изобразить в диаграмме Т – S обратимый и необратимый процессы истечения через сопло.

Вариант
Р1,МПа	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0	1.1	1.3	0.75	0.81	2.0
t1, °C
Р2,МПа	0.09	0.10	0.12	0.20	0.28	0.2	0.3	0.4	0.3	0.5	0.52	0.21	0.39	0.8
Fmin,мм2

 

Вариант
Р1,МПа	0.21	0.32	0.43	0.54	0.61	0.63	0.64	0.91	1.2	1.12	1.33	0.76	0.82	2.1
t1, °C
Р2,МПа	0.09	0.10	0.12	0.20	0.28	0.2	0.3	0.4	0.3	0.5	0.52	0.21	0.39	0.80
Fmin,мм2

 

Вариант
Р1,МПа	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0	1.1	1.3	0.75	0.81	2.0
t1, °C
Р2,МПа	0.08	0.09	0.11	0.19	0.27	0.19	0.29	0.37	0.29	0.47	0.51	0.19	0.29	0.82
Fmin,мм2

 

Вариант
Р1,МПа	0.22	0.31	0.41	0.52	0.62	0.71	0.82	0.92	1.02	1.13	1.34	0.77	0.83	2.1
t1, °C
Р2,МПа	0.09	0.10	0.12	0.20	0.28	0.2	0.3	0.4	0.3	0.5	0.52	0.21	0.39	0.80
Fmin,мм2

 

 

Пример расчета задачи

(дан для истечения двухатомной смеси газов)

Дано:

Р₁ =0,5 МПа; t₁=358°С; P₂= 0,19 МПа; F_MIN = 15мм²

Найти:

W₂, T_КР, v_кр, P_кр, G_кр, W_MAX, W_кр.

Решение:

1.Определим профиль сопла:

β = 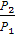= = 0,38<0,5 – используется сопло Лаваля (рис.1)

2. Определим скорость газовой смеси на выходе из сопла:

R = 2045 , Т₁ = 358°С = 631К, k = 1,36.

3. Определим критическую температуру (из уравнения адиабаты):

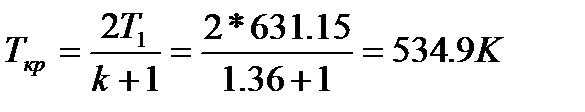
4. Находим удельный объем в первом сечении

Определим критический удельный объем

5. Находим критическое давление:

6. Находим расход газовой смеси

7. Находим максимально возможную скорость истечения:

8. Находим критическую скорость истечения:

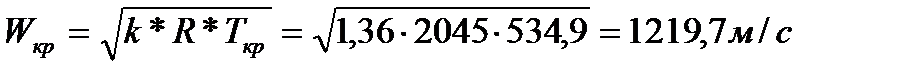
9. Удельный объем смеси на выходе:

10. Находим параметры сопла:

- минимальная площадь сечения сопла

-площадь выходного сечения сопла

- длина расширяющейся части сопла

принимаем угол конусности сопла α ≈ 12⁰

 

Тогда = 0,0038 м

 

 

Рисунок 2.2.4 – Сопло Лаваля

 

T

P₁ P₂

631,15 1

 

 

534,92

 

 

∆S

Рисунок 2.2.5

Расчет компрессора

Теоретические сведения

На рисунке2.3.1 в диаграмме pv изображены процессы, про­текающие в идеальном компрессоре. Линия 4—1 изобра­жает процесс всасывания газа, кривая 1—2 — процесс сжатия и линия 2—3 — процесс нагнетания. Диаграмму 1—2—3—4 называют теоретической индикаторной диа­граммой.

Теоретическая работа компрессора l ₀ определяется площадью индикаторной диаграммы и зависит от процесса сжатия (рисунок 2.3.2). Кривая 1—2 изображает процесс изотер­мического сжатия, кривая 1—2" — адиабатного сжатия и кривая 1—2' —политропного сжатия.

 

 

Рисунок 2.3.1 Рисунок 2.3.2

 

При изотермическом сжатии теоретическая работа компрессора равна изотермическому сжатию

(2.3.1)

Если масса всасываемого воздуха М кг, а объем его Vx м³, то

(2.3.2)

Работа, отнесенная к 1 м³ всасываемого воздуха,

(2.3.3)

Работа для получения 1 м³ сжатого воздуха

(2.3.4)

Количество тепла, которое должно быть отведено при изотермическом сжатии,

 

q = l₀ или Q = L₀.

 

При адиабатном сжатии теоретическая работа компрес­сора в k раз больше работы адиабатного сжатия:

(2.3.5)

 

Если масса всасываемого воздуха М кг, а объем его V_x м³, то

 

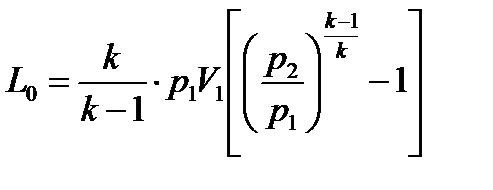(2.3.6)

Работа, отнесенная к 1 м³ всасываемого воздуха,

(2.3.7)

Работа для получения 1 м³ сжа­того воздуха

(2.3.8)

Температуру газа в конце cжатия можно определить из соотношения параметров адиабатного процесса. Работа компрессора при адиабатном сжатии может быть также найдена по формуле

l₀ = i₂– i₁ (2.3.9)

где i₁ и i₂ соответственно начальное и конечное значения энтальпии воздуха.

Эта формула весьма удобна для подсчета работы идеаль­ного компрессора при адиабатном сжатии с помощью диаграммыi– S.

В этом случае из точки 1 (рис. 2.3.3), характеризующей начальное состояние, проводят вертикальную линию до пересечения ее в точке 2 с изобарой р₂. Ординаты точек 1и 2 дают значения энтальпии i₁ и i₂ а отрезок1—2 —их разность.

 

Рисунок 2.3.3

 

При политропном сжатии теоретическая работа ком­прессора в nраз больше работы политропного сжатия:

(2.3.10)

 

Если масса всасываемого воздуха М кг, а объем его V_L ж³, то

(2.3.11)

Работа, затрачиваемая на сжатие 1 м³всасываемого воздуха,

(2.3.12)

Работа для получения 1 м³сжатого воздуха

(2.3.13)

Количество тепла, которое должно быть отведено при политропном сжатии, определяется по формуле:

 

Все приведенные выше формулы для определения ра­боты компрессора дают абсолютную величину работы.

Теоретическая мощность двигателя для привода ком­прессора определяется по формулам:

(2.3.14)

(2.3.15)

(2.3.16)

В формулах (2.3.1)—(2.3.16) значения p, v, l₀, L₀, даны соответственно в следующих единицах: p₁ и p₂ в н/мг²; v (объем всасываемого или сжатого воздуха) — в м³/ч; l₀ – в дж/ч; – в Дж/м³иN в кВт.

Действительная индикаторная диаграмма значительно отличается от теоретической главным образом вследствие наличия в действительном компрессоре вредного про­странства, потерь давления во впускном и нагнетатель­ном клапанах и теплообмена между газом и стенками цилиндра.

При наличии вредного пространства (рисунок2.3.4) в инди­каторную диаграмму вводится добавочный процесс (ли­ния 3 — 4) — процесс расширения сжатого газа, остав­шегося к концу нагнетания во вредном пространстве цилиндра.

 

 

Рисунок2.3. 4

Отношение объема вредного пространства к объему, описываемому поршнем, т. е. величину

;

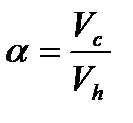называют относительной величиной вредного про­странства.

Вследствие наличия вредного пространства производительность ком­прессора уменьшается. Величину характеризующую степень полноты использования рабо­чего объема цилиндра, называют объемным к. п. д. ком­прессора.

 

(2.3.17)

Объемный к. п. д. компрессора можно также выразить через относительную величину вредного пространства и отношение давлений нагнетания и всасывания:

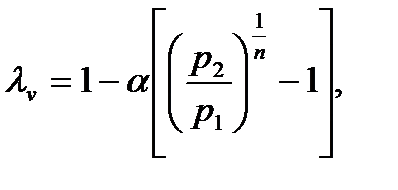(2.3.18)

где n- показатель политропы расширения газа, остав­шегося во вредном пространстве.

Теоретическая работа идеального компрессора яв­ляется минимальной. Действительную работу реального компрессора определяют при помощи изотермического или адиабатного к. п. д. и механического к. п. д.:

(2.3.19)

где l_из и l_ад — соответственно теоретическая работа компрессора при изотермическом и адиабатном сжатий, а l_к — действительная работа компрессора. Эти коэффициенты характеризуют степень совершенства действи­тельного процесса в сравнении с идеальным.

Механический к. п. д. учитывает механические потери в компрессоре. Произведение изотермического или адиабатного к. п. д. на механический называют эффективным

к. п. д. компрессора η_к = η_из ∙η_м = η_ад ∙ η_м;

 

Рис. 2.3.5 Рис. 2.3.6 Рис. 2.3.7.

 

Действительная мощность, потребляемая двигателем компрессора, для сжатия М кг/ч газа определяется по формуле

, (2.3.20)

С увеличением конечного давления объемный к. п. д.одноступенчатого компрессорауменьшается (рис. 2.3.5) и, сле­довательно, уменьшается также производительность компрессора. В пределе, когда кривая сжатия пересекает линию характеризующую объем вредного пространства, всасывание воздуха в цилиндр прекращается и, следовательно, объемный кпд. и производительность компрессора становятся равными нулю.

На рис. 2.3.6 и 2.3.7 показаны процессы сжатия в двух и трехступенчатом компрессоре.

Линии 1-2, 3 - 4 и 5 - 6изображают процесс адиабатного сжатия в каждом цилиндре компрессора, а линии 2—3 и 4—5 - процессы изобарного охлаждения воздуха в специальных холодиль­никах.

 

 

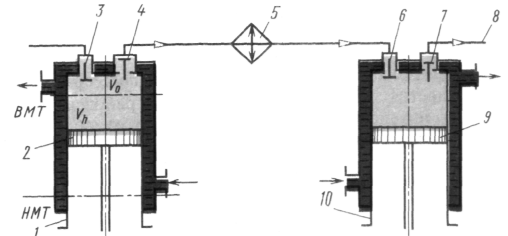
Рисунок2.3.8 - Схема двухступенчатого компрессора

 

Процесс сжатия воздуха (газа) в многоцилиндровых или многоступенчатых компрессорах осуществляется по­следовательно во всех цилиндрах с охлаждением воздуха после сжатия в каждом цилиндре. Обычно при этом стре­мятся к тому, чтобы воздух (газ) после холодильника имел ту же температуру, с которой он поступил в преды­дущую ступень. Таким образом, для трехступенчатого компрессора (рис. 2.3.7)

t₁= t₂ = t₃

Наиболее выгодным оказывается многоступенчатое сжа­тие в случае, если отношение давлений в каждой ступени прин