Тема 1: «Рациональные дроби и преобразование выражений»
1. 
 2.
2.

3.
 4.
4.
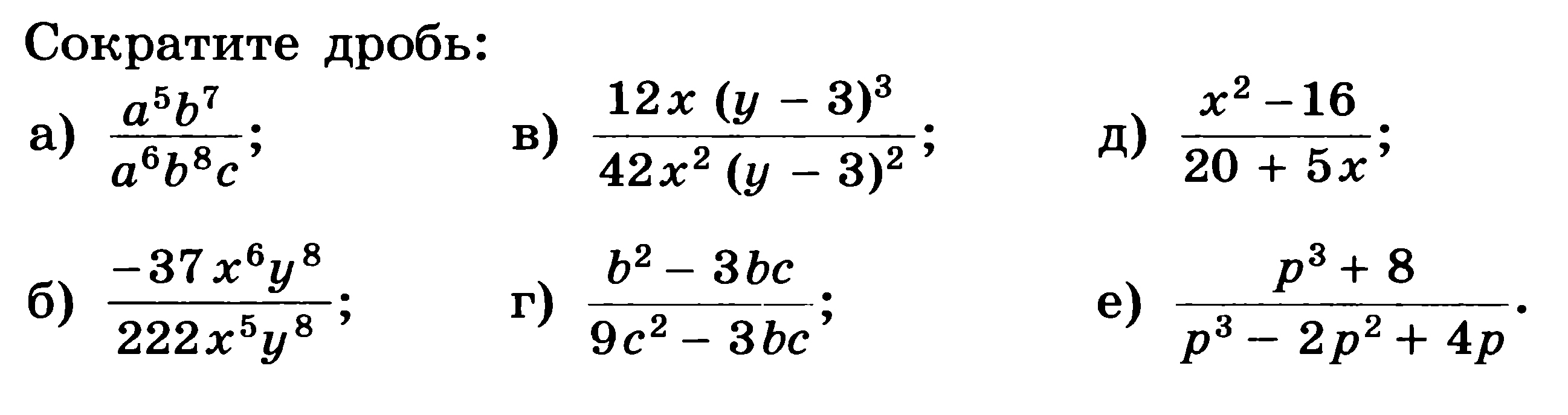
5.
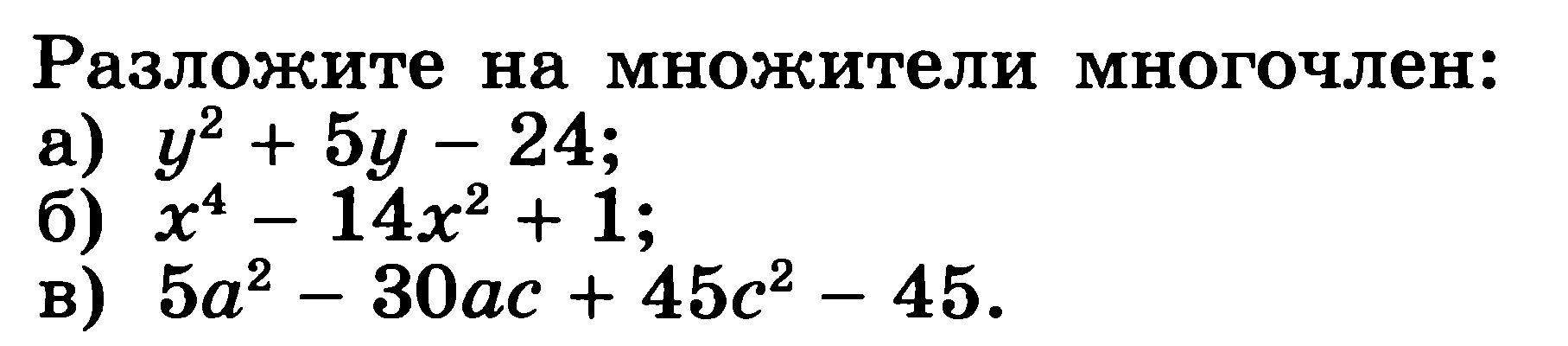 Тема 1_ Занятие 2: «Рациональные дроби и преобразование выражений»
Тема 1_ Занятие 2: «Рациональные дроби и преобразование выражений»
0.
 1.
1.

2.

3.

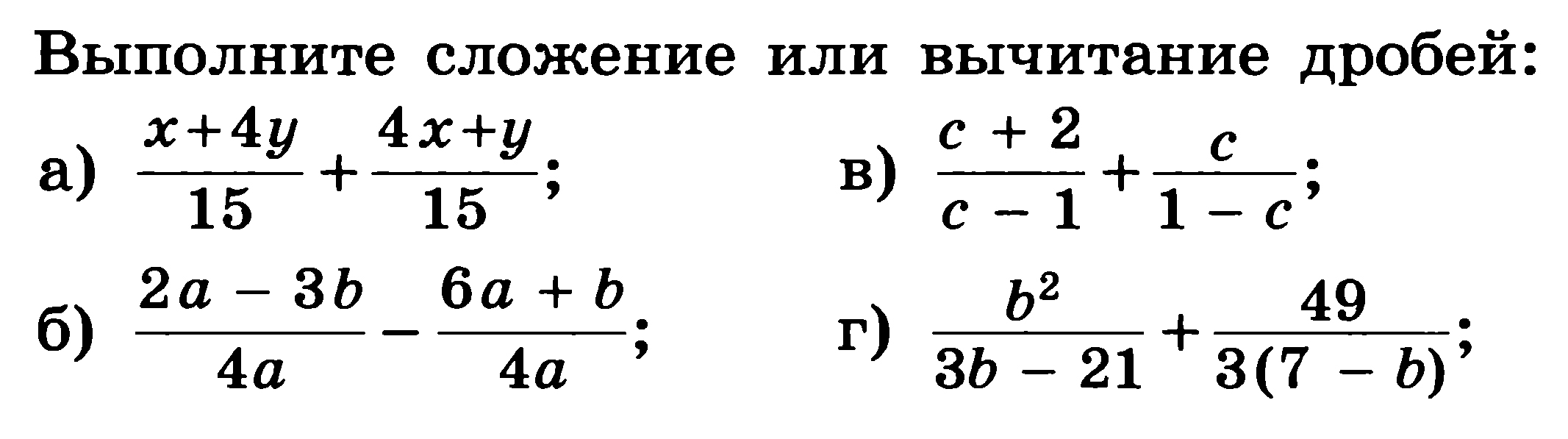 4.
4.
5.
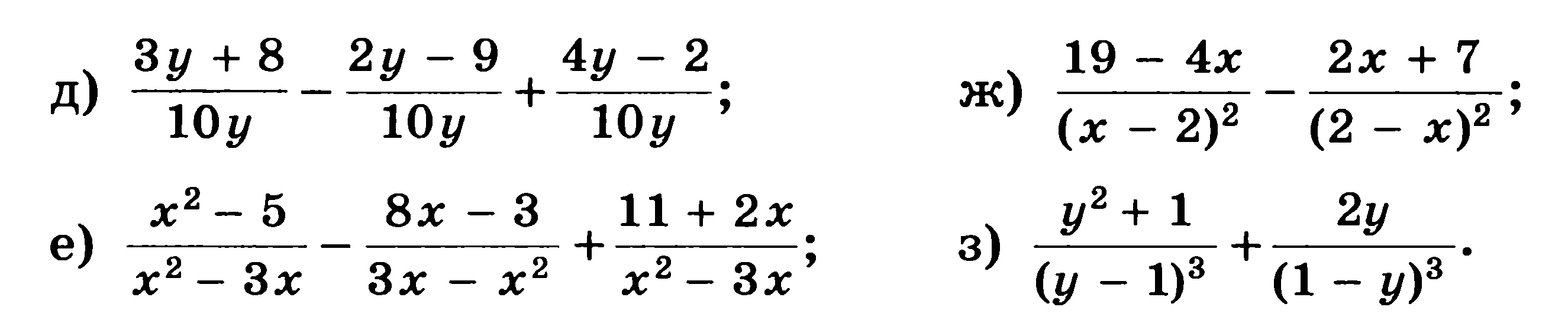
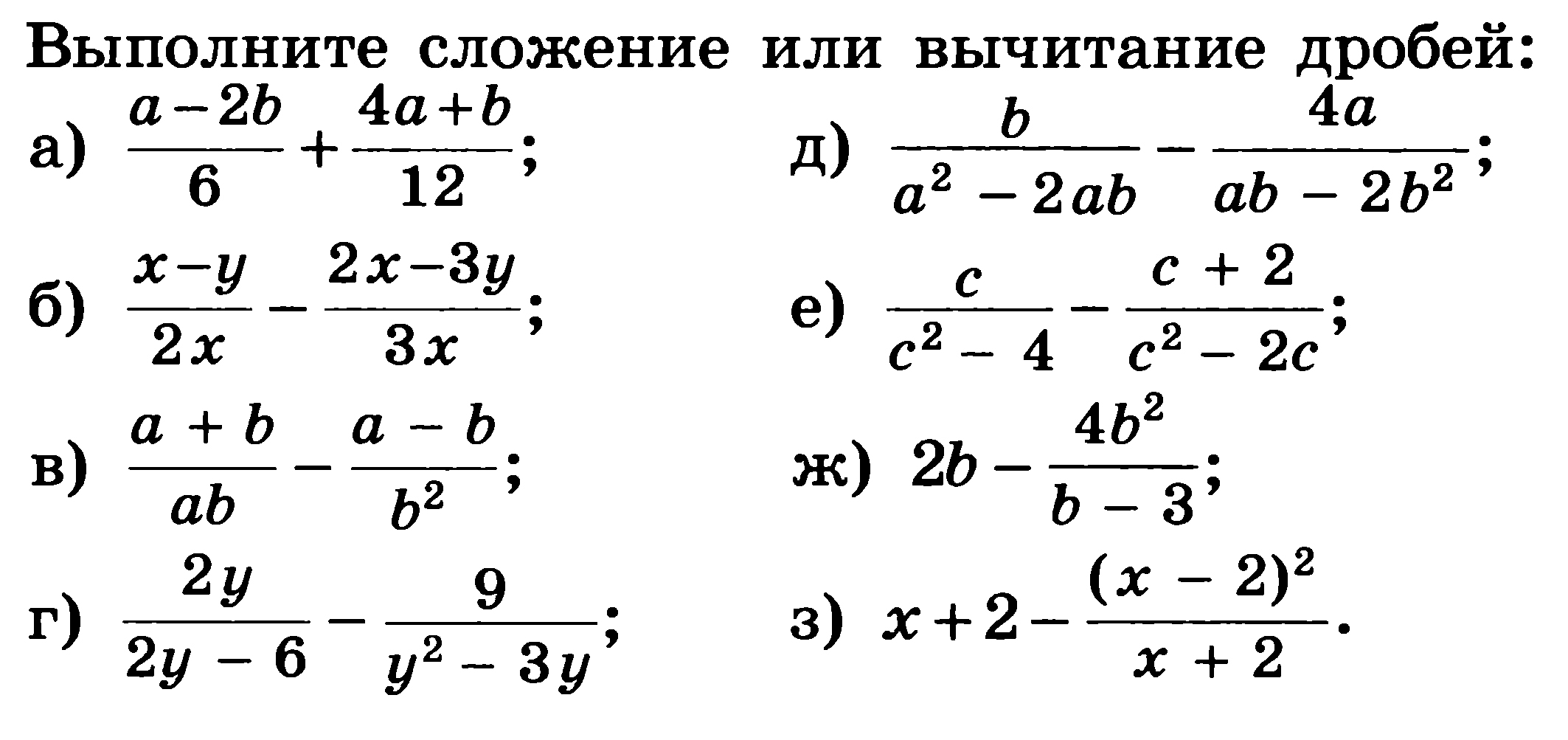
6.
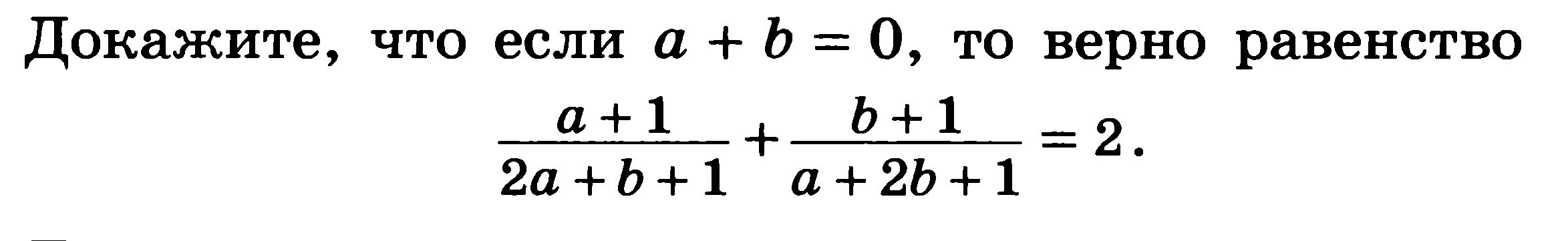 7.
7.

8.
Дополнительные задания к теме 1
1. Постройте график функции y=f(x), где

При каких значениях х функция принимает значения, меньше 2?
2. Постройте график функции

При каких значениях с прямая y=c имеет с графиком ровно две общие точки?
3. Найдите наименьшее значение выражения и значения х и у, при которых оно достигается  .
.
4. Найдите наименьшее значение выражения и значения х и у, при которых оно достигается  .
.
5. Постройте график функции  и найдите значения m, при которых прямая y=m имеет с ним ровно две общие точки.
и найдите значения m, при которых прямая y=m имеет с ним ровно две общие точки.
6. Постройте график функции 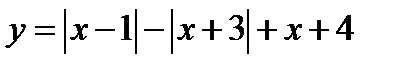 и найдите значения m, при которых прямая y=m имеет с ним ровно две общие точки.
и найдите значения m, при которых прямая y=m имеет с ним ровно две общие точки.
Тема 2: «Умножение и деление рациональных дробей. Рациональные уравнения»
| 1. | Выполните умножение

|
| 2. | Выплните деление

|
| 3. | 
|
| 4. | 
|
| 5. | 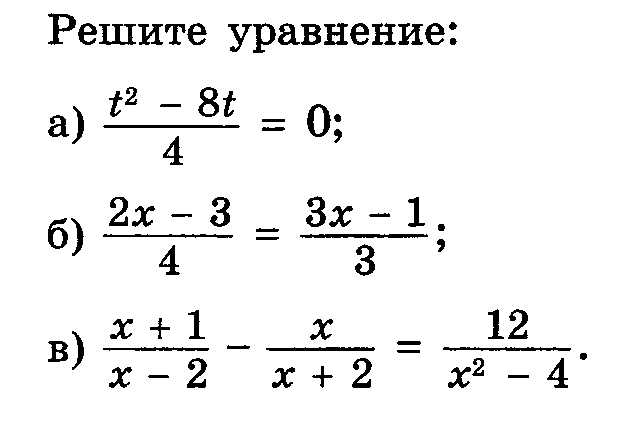
|
| 6. | Найдите наименьшее значение выражения (5х-4y+3)2+(3x-y-1)2 и значения х и у, при которых оно достигается. |
| 7. | Постройте график функции  и найдите значения k при которых прямая y=kx имеет с ним ровно одну общую точку. и найдите значения k при которых прямая y=kx имеет с ним ровно одну общую точку.
|
| Домашнее задание | |
| 1. | 
|
| 2. | 
|
| 3. | 
|
| 4. | 
|
| 5. | 
|
| 6. | Постройте график функции  и найдите значения k при которых прямая y=kx имеет с ним ровно одну общую точку. и найдите значения k при которых прямая y=kx имеет с ним ровно одну общую точку.
|
Дополнительные задания к теме 2
0. Упростите выражение

А)

Б)
1. 
Домашнее задание


Тема 3: «Действительные числа. Квадратные корни»
 1.
1.

2.
 3.
3.

4.

5.

6.

7.
 8.
8.

9.
Тема 4: «Свойства квадратных корней»
| 1. | 
|
| 2. | 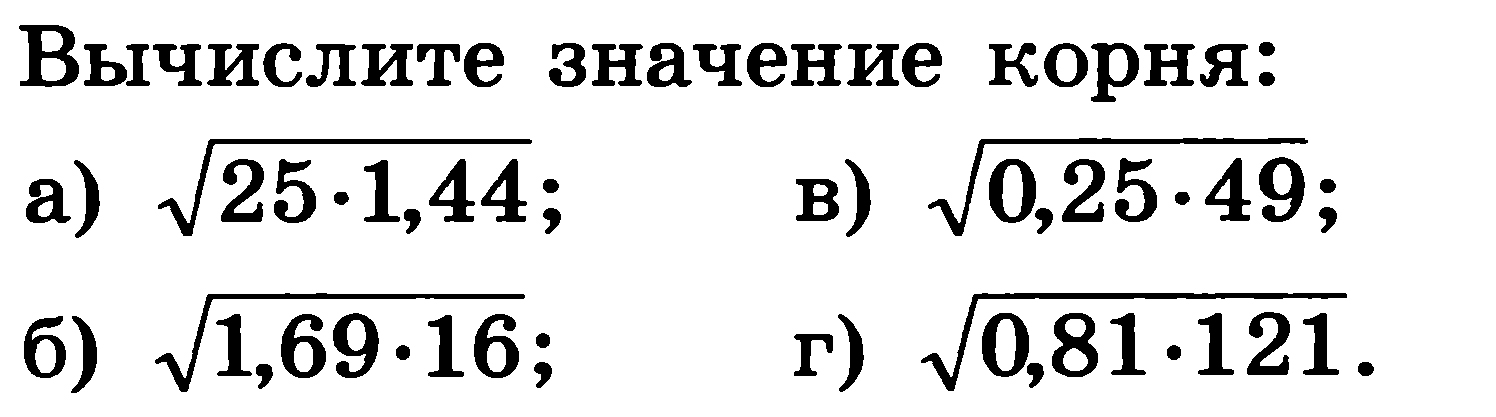
|
| 3. | 
|
| 4. | 
|
| 5. | 
|
| 6. | 
|
| 7. | 
|
| 8. | 
|
| 9. | 
|
| 10. | 
|
| 11. | 
|
Тема 5: «Преобразование выражений, содержащих квадратные корни»

| |

| |

| |

| |

| |

| |

| |

| |

|
| 11.01.16 | Квадратные уравнения: формула корней | |
| 18.01.16 | Квадратные уравнения: неполные квадратные уравнения, т. Виета | |
| 25.01.16 | Квадратные уравнения: Разложение квадратного трехчлена | |
| 01.02.16 | Квадратные уравнения: Задачи | |
| 08.02.16 | Квадратные уравнения: Задачи2 | |
| 15.02.16 | ||
| 22.02.16 | ||
| 29.02.16 | ||
| 07.03.16 | ||
| 14.03.16 | ||
| 21.03.16 | ||
| 04.04.16 | ||
| 11.04.16 | ||
| 18.04.16 | ||
| 25.04.16 | ||
| 16.05.16 | ||
| 23.05.16 | ||
| 30.05.16 |
Тема 6: «Квадратные уравнения: формула корней»
| 1. | Катеты прямоугольного треугольника меньше его гипотенузы соответственно на 2см и 4см. Чему равны длины сторон этого треугольника? |
| 2. | Решить уравнение методом выделения квадрата двухчлена
  
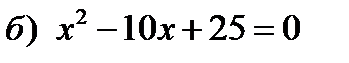  
  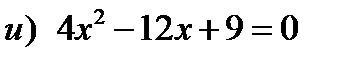
|
| 3. | 
|
| 4. | 
|
| 5. | 
|
| 6. | 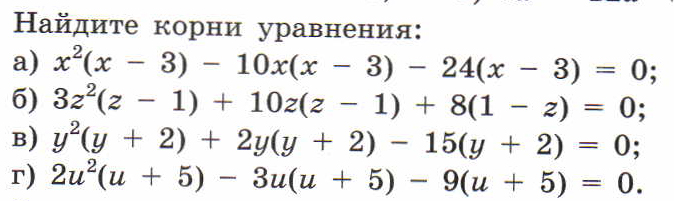
|
| 7. | 
|
Тема 7: «Метод замены переменных. Неполные квадратные уравнения. Теорема Виета»
| 0. | Покажите, что числа  и и  являются корнями квадратного уравнения являются корнями квадратного уравнения 
|
| 0.1 | Решите уравнение:
 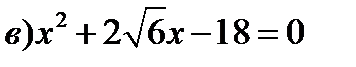
 
|
| 1. | Введите подходящую замену и решите уравнение:
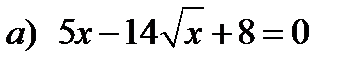 
 
 

|
| 2. | Решите уравнение:

|
| 3. | 
|
| 4. | 
|
| 5. | Решить уравнение: 

|
| 6. | 
|
| 7. | 
|
| 8. | 
|
Тема 8: «Разложение квадратного трехчлена на множители»
| 0. | 
|
| 0.1 | 
|
| 0.2 | 
|
| 0.3 | 
|
| 0.4 | 
|
| 1. | 
|
| 2. | Разложите на множители

|
| 3. | Разложите на множители

|
| 4. | 

|
| 5. | 
|
| 6. | Решите уравнение

|
Тема 9: «Решение текстовых задач. Задачи на движение»
А) Прямолинейное равномерное движение
Пример 1.
Из городов A и B, расстояние между которыми равно 330км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.
Пример 2.
Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в А, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
Б) Движение по замкнутой кривой
Пример 3.
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Пример 4.
Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
В) Движение по реке
Пример 5.
Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула
обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.