Диагностический инструментарий
по математике
10 класс
В соответствии с требованиями ФГОС СОО
Выполнил: Чеботарева Ф.М.
Кувандык, 2019 год
В настоящее время проблема самостоятельного успешного усвоения учащимися новых знаний, умений и компетенций, включая умение учиться, приоритетна. Большие возможности для этого представляет освоение универсальных учебных действий. Именно поэтому «Планируемые результаты» Стандартов второго поколения (ФГОС) определяют не только предметные, но и метапредметные (умственные действия учащихся, направленные на анализ и управление своей познавательной деятельностью), а также личностные результаты.
Важнейшим компонентом, входящим в функциональную математическую грамотность выступает математическая деятельность, успешность овладения приемами которой определяется соблюдением следующих требований к организации образовательного процесса: практико-ориентированный характер конструирования учебной информации; деятельностью способов и формы ее освоения; обеспечение условий для развития творческих способностей учащихся.
Задачи по формированию УУД на уроках математики в 10 классе
I. Регулятивные учебные действия обеспечивают возможность управления познавательной и учебной деятельностью посредством постановки целей, планирования, контроля, коррекции своих действий, оценки успешности усвоения.
Можно подобрать задания следующего типа: на планирование; на рефлексию; на принятие решения; на самоконтроль; на коррекцию.
Учебная дисциплина: алгебра и начала математического анализа.
Тема: «Тригонометрические уравнения»
Задание № 1. «Проблемная ситуация».
Цель: обучающийся самостоятельно учится выделять проблему, выдвигать гипотезу, определять цель своей деятельности, планировать её.
Форма выполнения задания: опережающее домашнее задание.
Описание задания. Создание проблемной ситуации на основе домашнего задания. За день до урока по теме «Арккосинус. Решение уравнения cos x = a » учащиеся получают задание решить уравнения: 
.
Решение уравнений осуществляется с помощью числовой окружности. При записи ответа для первых трёх уравнений учащиеся не испытывают трудностей, а вот в четвёртом уравнении возникает проблема – как записать ответ. Возникшее затруднение требует своего разрешения – это уже учебная проблема. Учащиеся высказывают свои гипотезы. На уроке учитель рассматривает гипотезы учеников, обобщает их, сообщает новые факты, направленные на обоснование выдвинутой гипотезы.
Задание № 2. «Преднамеренные ошибки».
Цель: ученик самостоятельно учится определять цель своей деятельности, планировать её самостоятельно двигаться по заданному плану, оценивать и корректировать полученный результат.
Форма выполнения задания: работа индивидуальная с последующей проверкой и коллективным обсуждением.
Описание задания. В задании надо найти ошибку в решении, объяснить на какое правило она допущена, предложить правильное решение тригонометрического уравнения.
а) 
Следовательно,
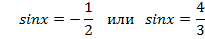
Используется формула корней для простейшего тригонометрического уравнения относительно косинуса – к уравнению относительно синуса. Не учитывается область значений 
).
б) 
Нарушение логики умозаключений, отсутствие логических вязок, рассмотрение одного частного случая верного равенства вместо решения уравнения, вычислительная ошибка.
в) 
Не учитывается область значений 
).
Задание № 3. «Оцениваем работу».
Цель: ученик самостоятельно учится оценивать и корректировать полученный результат.
Форма выполнения задания: работа индивидуальная с последующей проверкой и коллективным обсуждением.
Описание задания. В задании надо оценить работу (от 0 до 2 баллов), выполненную другим учащимся, при необходимости предложить правильное решение тригонометрического уравнения.
Варианты решения: 1-ый
Комментарий. Обоснованно получены верные ответы в обоих пунктах. 2 балла.
2-ой.
Комментарий.
Обоснованно получен верный ответ в пункте а, но отбор корней нельзя назвать обоснованным, так как перебор остановлен на корне, принадлежащем отрезку. 1 балл.
3-ий.
Комментарий.
Тригонометрическое уравнение решено неверно. Во второй строчке в правой части отсутствует знак минус – ошибка в формуле приведения. Пункт а не выполнен (не из-за вычислительной ошибки). 0 баллов.
Задание № 4. «Необходимая и достаточная информация».
Цель: ученик учится ставить себе конкретную цель, прогнозировать результат, планировать и организовывать деятельность для достижения поставленной цели.
Форма выполнения задания: работа индивидуальная с последующей проверкой и коллективным обсуждением.
Описание задания: Изучить задания под №13 для подготовки к ЕГЭ в различных источниках (учебная литература, образовательные сайты и т.п.). Составить справочник по теории, необходимой для успешного выполнения заданий №13. Требуется выделить значимую информацию.
II.Коммуникативные учебные действия обеспечивают возможности сотрудничества: умение слышать, слушать и понимать партнера, планировать и согласованно выполнять совместную деятельность, распределять роли, взаимно контролировать действия друг друга, уметь договариваться, вести дискуссию, правильно выражать свои мысли, оказывать поддержку друг другу и эффективно сотрудничать как с учителем, так и со сверстниками.
Можно подобрать задания следующего типа: на учёт позиции партнёра; на организацию и осуществление сотрудничества; на передачу информации и отображению предметного содержания; тренинги коммуникативных навыков; ролевые игры; групповые игры.
Учебная дисциплина: геометрия.
Тема: «Тела вращения»
Задание № 1. Кроссворд на тему «Тела вращения».
Цель: формирование коммуникативных действий, направленных на структурирование информации по данной теме, умение сотрудничать в процессе создания общего продукта совместной деятельности.
Форма выполнения задания: работа групповая с последующей взаимопроверкой и коллективным обсуждением.
Описание задания: при закреплении темы «Тела вращения. Площади поверхности» можно предложить учащимся составить кроссворды на эту тему, используя понятия и определения составляющих элементов (образующая, радиус, высота, сечение и так далее). Команды соперников отгадывают кроссворд (бонус команде, которая составила кроссворд с использованием большего количества терминов).
Задание № 2. «Составь задание партнеру».
Цель: формирование коммуникативных действий, направленных на умение сотрудничать в процессе обучения (закрепления материала).
Форма выполнения задания: работа в парах.
Описание задания: придумать задачи на вычисление элементов тел вращения, их поверхностей, площади сечения. Обучающиеся с высоким уровнем знаний составляют задачи по данной теме и предлагают решить их своим товарищам. Проверяется теоретический материал, и вырабатываются навыки решения задач по заданной теме, правильное применение формул.
III.Познавательные учебные действия включают действия исследования, поиска, отбора и структурирования необходимой информации, моделирование изучаемого содержания.
Можно подобрать задания следующего типа: задачи и проекты на выстраивание стратегии поиска решения задач; задачи и проекты на сравнение, оценивание; задачи и проекты на проведение эмпирического исследования; задачи и проекты на проведение теоретического исследования; задачи на смысловое чтение.
Учебная дисциплина: геометрия.
Тема: «Правильные многогранники»
Задание № 1. Работа с моделями.
Цель: уметь сравнивать, классифицировать объекты по выделенным признакам; обрабатывать, систематизировать и обобщать полученную информацию.
Форма выполнения задания: работа индивидуальная с последующей взаимопроверкой и коллективным обсуждением.
Описание задания. Выделить особую группу многогранников и дать понятие о правильных многогранниках.
1) Работа с моделями пространственных тел.
− Отложите в коробку те модели, которые не являются моделями многогранников.
− Уберите в коробку модели невыпуклых многогранников.
− Прочитайте определение правильного многогранника.
− Оставьте на столе только модели правильных многогранников.
2) Отметить признаки правильного многогранника символом «х»:
□ Выпуклость многогранника.
□ Все грани – равные правильные многоугольники.
□ Все грани – правильные многоугольники с одним и тем же числом сторон.
□ Равны все ребра.
□ Равны все двугранные углы.
□ Равны все плоские углы.
□ Равны все многогранные углы.
Задание № 2. Частично–поисковая работа.
Цель: уметь сравнивать, классифицировать объекты по выделенным признакам; обрабатывать, систематизировать и обобщать полученную информацию.
Форма выполнения задания: работа индивидуальная с последующей взаимопроверкой и коллективным обсуждением.
Описание задания. Учитель перед учениками ставит проблему: Много ли существует видов правильных многогранников? Предлагает высказать различные предположения о том, как установить количество видов правильных многогранников? Для рациональной организации учебной деятельности предлагается заполнить таблицу.
I Грань –
an – внутренний угол правильного n – угольника.
a = ____
n – число граней многогранного угла.
1). n = 3 ______________________________ Вывод:
2). n = 4 ______________________________
3). n = 5 ______________________________
4). n = 6 ______________________________
I I. Грань –
a = ____
1). n = 3 ______________________________ Вывод:
2). n = 4 ______________________________
3). n = 5 ______________________________
4). n = 6 ______________________________
I I I. Грань –
a = ____
1). n = 3 ______________________________ Вывод:
2). n = 4 ______________________________
3). n = 5 ______________________________
4). n = 6 ______________________________
I V. Грань –
a = ____
1). n = 3 ______________________________ Вывод:
2). n = 4 ______________________________
3). n = 5 ______________________________
V. Грань –
a = ____
1). n = 3 ______________________________ Вывод:
2). n = 4 ______________________________
Вывод:
Результат работы:
I. Грань – правильный треугольник.
a3 – внутренний угол треугольника.
a3 = 60°
n – число граней многогранного угла.
1). n = 3 60° · 3 = 180° < 360° Вывод: Существует 3 вида
2). n = 4 60° · 4 = 240° < 360° правильных многогранников,
3). n = 5 60° · 5 = 300° < 360° гранями которых являются
4). n = 6 60° · 6 = 360° (многогранный правильные треугольники.
угол совпадает с плоскостью)
 Рис. 1
Тетраэдр Октаэдр Икосаэдр
|
I I. Грань – квадрат.
a4 = внутренний угол квадрата.
a4 = 90°
1). n = 3 90° · 3 = 270° < 360° Вывод: Существует 1 вид
2). n = 4 90° · 4 = 360° (многогранный правильного многогранника,
 угол совпадает с плоскостью) гранями которого являются
квадраты.
Куб (гексаэдр).Рис 2.
|
I I I. Грань – правильный пятиугольник.
a5 = 180° · (5 – 2) / 5 = 108°
1).n = 3 108° · 3 = 324° < 360° Вывод: Существует 1 вид
2).n = 4 108° · 4 = 432° > 360° правильного многогранника,
гранями которого являются
правильные пятиугольники.
Рис. 3. Додекаэдр
I V. Грань – правильный шестиугольник.
a6 = 120° Вывод: правильный многогранник
1).n = 3 120° · 3 = 360° (многогранный гранями которого являются
гол совпадает с плоскостью) правильные шестиугольники
не существует.
Вывод: существует 5 видов правильных многогранников.
|
Задание № 3. Исследование.
Цель: учиться выдвигать и обосновывать гипотезы, самостоятельно находить способы решения проблем творческого и поискового характера, проводить эмпирические и теоретические исследования.
Форма выполнения задания: работа индивидуальная с последующей взаимопроверкой и коллективным обсуждением.
Описание задания. Постановка проблемы исследования: « С незапамятных времен тянется история драгоценных кристаллов. Пример тому – история одного из самых замечательных алмазов – алмаза «Кохинор». Первые известия об этом алмазе приходят к нам из Древней Индии. Многие века он был родовой ценностью раджей. Но в 1526 году бесценный камень оказался в руках могущественных Моголов. И с тех пор стал камнем раздора. И вот в 1739 году персидский хан Надир обманом узнал, что владелец камня Великий Могол Мухаммед носит алмаз в тюрбане. При прощальном визите шах Надир предложил в знак вечной дружбы обменяться тюрбанами. Когда новый хозяин размотал тюрбан и увидел алмаз, он воскликнул «Кох и нур!», что означает «гора света». В 1848 году алмаз попал как военный трофей в сокровищницу английской короны. Английская королева дала указание сделать огранку вдоль ребер алмаза золотой нитью. Но огранка не была сделана, так как ювелир не сумел рассчитать максимальную длину золотой нити, а сам алмаз ему не показали. Ювелиру были сообщены следующие данные: число вершин В=54, число граней Г=48, длина наибольшего ребра L= 4мм». А вы сумеете найти максимальную длину золотой нити?
Проблема: Найти число ребер алмаза (выпуклого многогранника).
Тема: Зависимость между числами вершин, граней и ребер выпуклого многогранника.
Цель: Выявить зависимость между числами вершин, граней и ребер выпуклого многогранника.
Гипотеза: Если существует зависимость между числами вершин, граней и ребер, то ее можно выразить формулой и по ней найти число ребер выпуклого многогранника.
Эксперимент: Заполняется таблица. Выявляется зависимость.
Если учащиеся затрудняются в установлении зависимости, то учитель руководит их действиями (сравните числа вершин, граней и ребер для каждого многогранника; установите зависимость; проанализируйте получившиеся результаты; сделайте обобщение; сформулируйте вывод).
| Название правильного многогранника | Вид грани | Число вер-шин (В) | Число гра- ней (Г) | Число ребер (Р) | Вывод из наблюдений |
| Четырехгранник (тетраэдр) | правильный треугольник | В+Г=Р+2 | |||
| Шестигранник (куб-гексаэдр) | квадрат | В+Г=Р+2 | |||
| Восьмигранник (октаэдр) | правильный треугольник | В+Г=Р+2 | |||
| Двенадцатигранник (додекаэдр) | правильный пятиугольник | В+Г=Р+2 | |||
| Двадцатигранник (икосаэдр) | правильный треугольник | В+Г=Р+2 |
«Теорема носит название Декарта – Эйлера. Эйлер нашел и проверил эту зависимость. За сто лет до Эйлера эта теорема была сформулирована Декартом, но не доказана. Теорема верна не только для правильных многогранников, но и для любых выпуклых многогранников и даже для некоторых невыпуклых».
Задание № 4. Поиск и обработка информации.
Цель: учиться выполнять поиск и выделение необходимой информации; применять различные методы информационного поиска, в том числе с помощью компьютерных средств.
Форма выполнения задания: работа индивидуальная с последующим отчетом перед классом.
Описание задания. 1.Прочитать содержание §9 (стр.53-54,56). 2.Подготовить короткое сообщение с демонстрацией минералов. 3.Заполнить таблицу (под каждым прямоугольником напишите кристаллы каких минералов используются). Литература: С.И.Кабардин, Н.И.Шедер. Факультативный курс физики. – М.:Просвещение, 1989 г. (дополнительная литература на усмотрение обучающегося).
IV. Личностные учебные действия позволяют сделать учение осмысленным, увязывая его с реальными жизненными целями и ситуациями. Личностные действия направлены на осознание, исследование и принятие жизненных ценностей, позволяют сориентироваться в нравственных нормах и правилах, выработать свою жизненную позицию в отношении мира.
Можно подобрать задания следующего типа: на личностное самоопределение; на развитие Я-концепции; на смыслообразование; на мотивацию; на нравственно-этическое оценивание.
Учебная дисциплина: алгебра и начала анализа.
Тема: «Решение задач на сложные проценты».
Задание № 1. Творческие задания, имеющие практическое применение (в рамках урока с элементами игры «Компетентность», который содержит мини-исследования и проект).
Цель: преодолевать в сознании учеников неизбежно возникающее представление о формальном характере предмета, оторванности от жизни и практики; обучающимся научиться задаваться вопросом о том, «какое значение, смысл имеет для меня учение», и уметь находить ответ на него; уметь ориентироваться в социальных ролях и межличностных отношениях.
Форма выполнения задания: работа в группах с последующим отчетом.
Описание задания. Дидактическая игра «Компетентность». «Решение одной задачи».
«Отдел экономики и строительства». Вы являетесь группой менеджеров отдела экономики крупной строительной фирмы. Ваша фирма получила предложение вложить 9 000 000 долларов в строительство моста, эксплуатация которого будет в течение 15 лет приносить ежегодный доход 810 000 долларов, выплачиваемый в конце года. Банковская ставка р=3% не будет меняться в течение всего срока. Выясните, выгоден ли этот проект, т.е. сравните сегодняшние затраты – 9 000 000 долларов – с завтрашними доходами по 810000 долларов ежегодно в течение 15 лет.
Частное предприятие «Такси». Вы предполагаете приобрести новый автомобиль, который станет приносить ежегодно чистый доход 2000$ в течение 7 лет, а затем будет продан за 1000$. Какую сумму вы будите готовы уплатить за автомобиль при банковской ставке 12%?
Члены родительского комитета. За обучение в музыкальной школе родители ежемесячно платят 300 рублей в течение 10 месяцев, внося плату в начале каждого месяца. Администрация школы заинтересована в том, чтобы получить первого сентября как можно больше наличных денег, и поэтому предлагает родителям заплатить сразу 2800 рублей и больше в течение года за обучение не платить. Банковская ставка составляет 3% в месяц. Кому выгоднее один раз в год заплатить 2800 рублей: администрации или родителям?