Билет 8
Числовые неравенства и их свойства
Числовое неравенство – это неравенство, в записи которого по обе стороны от знака неравенства находятся числа или числовые выражения.
Шар. Сфера
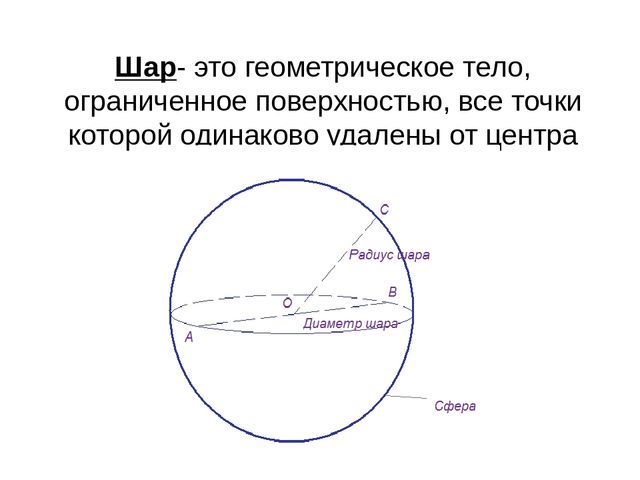
Сфера-это поверхность шара.
У шара Можно найти объем 
У сферы можно найти площадь
Билет 9
Числовые промежутки
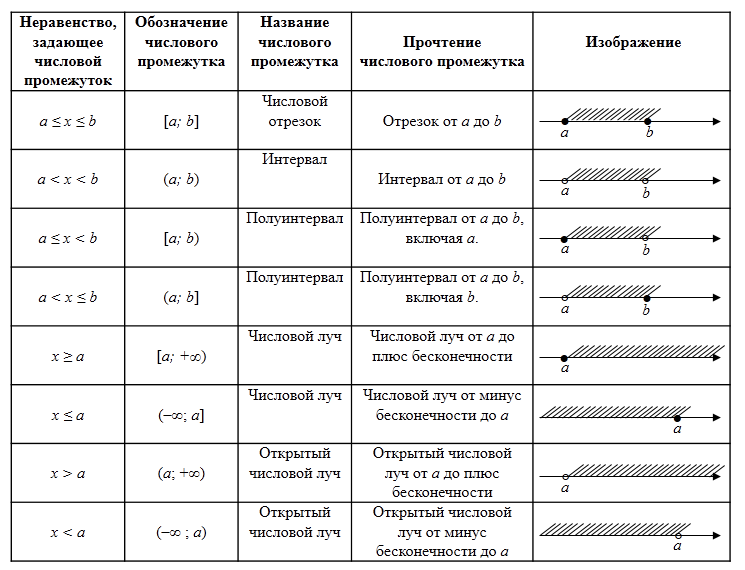
Множество чисел справа от точки a, отвечающих неравенству x > a, называется открытым числовым лучом. Обозначается так:
(a; +∞)
Читается так: открытый числовой луч от a до плюс бесконечности.
Множество чисел слева от точки a, отвечающих неравенству x < a, называется открытым числовым лучом от минус бесконечности до a.
Обозначается так:
(–∞; a)
Читается так: открытый числовой луч от минус бесконечности до a.
Теперь представим луч с точкой a, справа и слева от которой – множество чисел.
Множество чисел справа от точки a, отвечающих условию x ≥ a, называется числовым лучом.
Обозначается так:
[ a; +∞)
Читается так: числовой луч от a до плюс бесконечности.
Множество чисел слева от точки a, отвечающих условию x ≤ a, называется числовым лучом от минус бесконечности до a.
Обозначается так:
(–∞; a ]
Читается так: числовой луч от минус бесконечности до a.
Множество чисел, отвечающих условию a < x < b, называется интервалом. Обозначается так:
(a; b)
Читается так: интервал от a до b.
Представим на координатной прямой числа a и b, а также число x между ними.
Множество всех чисел, отвечающих условию a ≤ x ≤ b, называется числовым отрезком или просто отрезком. Обозначается так:
[ a; b ]
Читается так: отрезок от a до b.
Масштаб. Определение и примеры
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
|
|
Расстояние между точками – это длина отрезка, соединяющего эти точки
Например 1:2000 ОЗНАЧАЕТ ЧТО ОДНА ЕДИНИЦА ИЗМЕРЕНИЯ НА СХЕМЕ СООТВЕТСТВУЕТ ДВУМ ТЫСЯЧАМ.
Например, если на схеме отрезок имеет длину 1 см, это значит что на самом деле длина этого отрезка-2000 см
Кратчайшее расстояние между двумя точками- это длина отрезка прямой, соединяющего эти точки.
Билет 10
Прямоугольная система координат
Прямоугольная система координат образуется пересечением на плоскости двух перпендикулярных координатных прямых так, что положительная полуось одной направлена вправо (ось x, или ось абсцисс), а второй — вверх (ось y, или ось ординат).
точка 0 каждой из них и называется началом координат.
Возьмем на координатной плоскости 0 ху произвольную точку М. Опустим из нее перпендикуляры на оси координат. На осях получим точки М 1 и М 2 – проекции точки М соответственно на ось 0 х и 0 у
ОСЕВАЯ СЕМЕТРИЯ
Тоже самое что и в 5 билете
Билет 11
Вычитание рациональных чисел
Вычитание рациональных чисел зависит от знаков чисел уменьшаемого н вычитаемого.
1 Правило. Чтобы из одного числа вычесть другое, достаточно к уменьшаемому прибавить число, противоположное вычитаемому.
Например: -102 — (-80) = -102 + 80 = -22.
2 Правило. Если уменьшаемое — отрицательное число, а вычитаемое — положительное число, то нужно сложить модули уменьшаемого и вычитаемого и перед полученным результатом поставить знак «-».
|
|
Например: -839 — 71 = — (|-839|+|-71|) = — (839+71) = -910.
3 Правило. Если уменьшаемое — положительное число н вычитаемое — положительное число, то нужно найти разность модулей уменьшаемого и вычитаемого и перед полученным результатом поставить знак «-», если модуль уменьшаемого меньше модуля вычитаемого. Если модуль уменьшаемого равен модулю вычитаемого, то разность равна нулю.
Примеры.
0,165 — 0,015 = 0,15 т. к. |0,1б5| > |0,0151
1 307 — 1 307 = 0 т. к. |1 307| = |1 307|