Работа выполняется в Exce l
Исходные данные.
Заданы две выборки двух случайных величин Х1 и Х2, объемы выборок N1 и N2 соответственно.
Определение основных характеристик двух выборок.
Для каждой из выборок необходимо определить:
выборочное среднее Х1ср и Х2ср (воспользоваться функцией Excel СРЗНАЧ);
выборочное среднеквадратичное (стандартное) отклонение S1 и S2 (воспользоваться функцией Excel СТАНДОТКЛОН);
коэффициент вариации по формуле:


выборочную дисперсию S12 и S22;
определение доверительных интервалов для средних:
коэффициент Стьюдента t 1 (p1,β), t 2 (p2,β)
здесь р1 и р2 – число степеней свободы, в данном случае р1 = N1, р2 = N2,
β – доверительная вероятность, выбирается одно из трех значений:
β =0,8; β =0,9; β =0,95.
Для определения коэффициента Стьюдента воспользоваться функцией Excel СТЬЮДРАСПОБР.
Доверительные границы для средних:
нижние


верхние
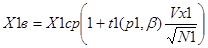

Проверка крайних значений на принадлежность к выборкам.
Для каждой из выборок:
отбрасываем максимальные значения;
определяем основные характеристики выборок с отброшенными значениями
выборочные средние Х1ср’ и Х2ср’,
выборочные среднеквадратичные отклонения S1’ и S2’;
коэффициенты вариации:


коэффициенты Стьюдента t 1’ (p1’,β), t 2’ (p2’,β)
здесь р1’ = N1-1, р2’ = N2-1;
Доверительные границы для средних:
нижние


верхние


Если выполняются условия:
 , а
, а  и
и  ,
,
то гипотеза о непринадлежности крайнего значения к первой выборке отвергается и дальше выборка должна рассматриваться полностью; в противном случае гипотеза принимается и дальше выборка должна рассматриваться без крайнего значения.
То же для второй выборки.
Если выполняются условия:
 , а
, а  и
и  ,
,
то гипотеза о непринадлежности крайнего значения ко второй выборке отвергается и дальше выборка должна рассматриваться полностью; в противном случае гипотеза принимается и дальше выборка должна рассматриваться без крайнего значения.
Далее то же выполняется для минимальных значений, при этом, если принята гипотеза о непринадлежности максимальных значений к выборкам, исходные выборки рассматриваются без этих значений.
Проверка возможности объединения двух выборок.
Проверка гипотезы о равенстве двух дисперсий.
Эмпирический критерий Фишера:
 , где
, где  - большее значение из двух S12 и S22, соответственно
- большее значение из двух S12 и S22, соответственно  - меньшее значение. Если выполняется условие
- меньшее значение. Если выполняется условие  , то гипотеза о равенстве дисперсий может быть принята.
, то гипотеза о равенстве дисперсий может быть принята.
Здесь α – уровень значимости, выбирается одно из трех значений: α=0,1; α=0,05; α=0,01.
nб=Nб-1, nм=Nм-1, а Nб, Nм – объемы выборок, соответствующих большему и меньшему значению дисперсий.
 - квантиль распределения Фишера, определяется с использованием функции Excel FРАСПОБР.
- квантиль распределения Фишера, определяется с использованием функции Excel FРАСПОБР.
Проверка гипотезы о равенстве двух средних.
Эмпирический критерий Стьюдента:
 ,
,
где  - стандартная ошибка разности средних значений:
- стандартная ошибка разности средних значений:

Если выполняется условие  , то гипотеза о равенстве средних значений может быть принята.
, то гипотеза о равенстве средних значений может быть принята.
Здесь r=N1+N2-2 – число степеней свободы.
Если приняты обе гипотезы – о равенстве дисперсий и средних, то две выборки могут быть объединены. В этом случае определяются общие среднее значение и стандартное отклонение объединенной выборки.
Пример расчета.
| Х1 | Х2 | ||||||||
| N1 | N2 | ||||||||
| X1cp | 10245,62 | X2cp | 5654,678 | ||||||
| S1 | 4756,955 | S2 | 3304,806 | ||||||
| S1^2 | S2^2 | ||||||||
| Vx1 | 0,464291 | Vx2 | 0,584437 | ||||||
| β | 0,9 | β | 0,9 | ||||||
| t1(p1,β) | 1,295585 | t2(p1,β) | 1,296066 | ||||||
| X1н | 9456,527 | X2н | 5097,047 | ||||||
| X1в | 11034,72 | X2в | 6212,309 | ||||||
| Отбрасываем минимальные значения | |||||||||
| X1min | X2min | ||||||||
| N1' | N2' | ||||||||
| X1cp' | 10405,15 | X2cp' | 5743,224 | ||||||
| S1' | 4629,629 | S2' | 3262,307 | ||||||
| S1'^2 | S2'^2 | ||||||||
| Vx1' | 0,444936 | Vx2' | 0,568027 | ||||||
| β | 0,9 | β | 0,9 | ||||||
| t1'(p1,β) | 0,126194 | t2'(p1,β) | 0,126222 | ||||||
| X1н' | 10329,73 | X2н' | 5689,155 | ||||||
| X1в' | 10480,57 | X2в' | 5797,293 | ||||||
| Условие | 
| ||||||||
| не выполняется | |||||||||
| │X1н'-X1cp│/X1cp | 0,008209 | ||||||||
| │X1в'-X1cp│/X1cp | 0,022931 | ||||||||
| Невыполнение хотя бы одного из трех условий | |||||||||
| свидетельствует о необходимости отбрасывания | |||||||||
| значения 674 первой выборки. | |||||||||
| Условие | 
| ||||||||
| не выполняется | |||||||||
| │X2н'-X2cp│/X2cp | 0,006097 | ||||||||
| │X2в'-X2cp│/X2cp | 0,025221 | ||||||||
| Невыполнение хотя бы одного из трех условий | |||||||||
| свидетельствует о необходимости отбрасывания | |||||||||
| значения 519 второй выборки. | |||||||||
| Характеристики выборок с отброшенными | ||||
| минимальными значениями | ||||
| N1 | N2 | |||
| X1cp | 10405,15 | X2cp | 5743,224 | |
| S1 | 4629,629 | S2 | 3262,307 | |
| S1^2 | S2^2 | |||
| Vx1 | 0,444936 | Vx2 | 0,568027 | |
| β | 0,9 | β | 0,9 | |
| t1(p1,β) | 0,126194 | t2(p1,β) | 0,126222 | |
| X1н | 10329,73 | X2н | 5689,155 | |
| X1в | 10480,57 | X2в | 5797,293 | |
| Отбрасываем максимальные значения | ||||
| X1max | X2max | |||
| N1' | N2' | |||
| X1cp' | 10220,68 | X2cp' | 5573,526 | |
| S1' | 4441,397 | S2' | 3022,023 | |
| S1'^2 | S2'^2 | |||
| Vx1' | 0,43455 | Vx2' | 0,54221 | |
| β | 0,9 | β | 0,9 | |
| t1'(p1,β) | 0,126203 | t2'(p1,β) | 0,126222 | |
| X1н' | 10147,7 | X2н' | 5523,002 | |
| X1в' | 10293,65 | X2в' | 5624,05 | |
| Условие | 
| |||
| не выполняется | ||||
| │X1н'-X1cp│/X1cp | 0,024742 | |||
| │X1в'-X1cp│/X1cp | 0,010716 | |||
| Невыполнение хотя бы одного из трех условий | ||||
| свидетельствует о необходимости отбрасывания | ||||
| максимального значения первой выборки. | ||||
| Условие | 
| |||
| не выполняется | ||||
| │X2н'-X2cp│/X2cp | 0,038345 | |||
| │X2в'-X2cp│/X2cp | 0,02075 | |||
| Невыполнение хотя бы одного из трех условий | ||||
| свидетельствует о необходимости отбрасывания | ||||
| максимального значения второй выборки. | ||||
| Характеристики выборок с отброшенными | ||||
| максимальными и минимальными значениями | ||||
| N1 | N2 | |||
| X1cp | 10220,68 | X2cp | 5573,526 | |
| S1 | 4441,397 | S2 | 3022,023 | |
| S1^2 | S2^2 | |||
| Проверка возможности объединения двух выборок | ||||
| Проверка равенства дисперсий | ||||
| Эмпирический критерий Фишера | ||||
| Fe | 2,15995 | |||
| α | 0,1 | |||
| nб | nм | |||
| Квантиль распределения F(α,nб,nм) | ||||
| 1,404371 | ||||
| Fe> F(α,nб,nм) | ||||
| Гипотеза о равенстве дисперсий отвергается | ||||
| Проверка равенства средних | ||||
| σ(х1-х2) | 65,71332 | |||
| Эмпирический критерий Стьюдента | ||||
| te | 70,71857 | |||
| r | ||||
| t(α,r) | 1,65833 | te>t(α,r) | ||
| Гипотеза о равенстве средних отвергается | ||||
| Выборки не могут быть объединены |
| Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | |||||||||
| Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | |||||||||
| Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | |||||||||
| Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | |||||||||
| Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | |||||||||
| < |
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2019-03-17 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд