Согласно закону Ома в комплексной форме, комплексным сопротивлением 
элемента в цепи синусоидального тока является отношение комплекса напряжения на элементе к комплексу тока, протекающего через элемент, т.е.
;
Комплексное сопротивление обозначается буквой z, с чертой снизу, указывающей на комплексный характер величины. Пусть заданы в общем виде комплекс действующего значения напряжения на элементе и комплекс действующего значения тока, протекающего через элемент:
;
;
Тогда комплексное сопротивление элемента запишется в виде:
;
Где Z – модуль комплексного сопротивления элемента;
- сдвиг по фазе, вносимый элементом.
Алгебраические операции с комплексными числами, векторная диаграмма
Изобразим комплексное число 
как вектор на комплексной плоскости (рис.2.1), где b – это проекция вектора на действительную ось, c - это проекция вектора на мнимую ось.
Очевидно, что алгебраическая форма записи комплексного числа определяет вектор в декартовых координатах.
Этот же вектор можно задать, определив его модуль r и угол между направлением вектора и положительным направлением действительной оси φ, т.е. определить вектор в полярных координатах (рис.2.1). Для этого воспользуемся показательной формой записи комплексного числа, т.е. 
. Угол φ отсчитывается против часовой стрелки от положительного направления действительной оси.
Переход от алгебраической формы к показательной выполняется по формулам, следующим из рис.1.1:
, где 
Обратный переход от показательной формы к алгебраической следует из формулы Эйлера:
, где 
Рисунок 1.1
Векторной диаграммой называется совокупность векторов ЭДС, напряжений и токов, изображенных в одной системе координат. Наиболее распространенным типом векторной диаграммы является диаграмма, которая содержит на комплексной плоскости комплексы действующих значений ЭДС, напряжений и токов.
Пример 2
Построить векторную диаграмму напряжений и токов на участке цепи, если известно, что: 
(В), 
(А).
Решение
Представим комплексы напряжений и токов в алгебраической форме:
Рисунок 1.2
Изобразим их на комплексной плоскости, задаваясь для каждого вектора значениями его проекций на действительную и мнимую оси, либо модулем вектора и углом между направлением вектора и положительным направлением действительной оси. Векторная диаграмма показана на рис.1.2.
Если заданы два комплексных числа 
и 
, то их суммой будет следующее комплексное число:
;
При сложении комплексных чисел отдельно суммируются их действительные и мнимые части. Очевидно, что удобно суммировать комплексные числа, представленные в алгебраической форме.
Пример 3
Известны комплексные сопротивления ветвей: 
и 
. Найти их сумму.
Решение
;
Умножение комплексных чисел, заданных в алгебраической форме, осуществляется почленным перемножением их действительных и мнимых частей:
; т.к. 
;
Пример 4
Известны комплексные сопротивления ветвей: и . Найти их произведение.
Решение
.
В случае если необходимо разделить два комплексных числа и 
, заданных в алгебраической форме, например:
;
то для того, чтобы представить искомое комплексное число 
в алгебраической форме, необходимо умножить и числитель, и знаменатель этого числа на сопряженное комплексное значение знаменателя 
.
Числом , комплексно сопряженным с числом 
, называется число, отличающееся от исходного знаком мнимой части, т.е. 
.
Таким образом
;
;
где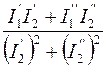 
- действительная часть комплексного числа ;
- мнимая часть комплексного числа .
Пример 5
Известны комплексные сопротивления ветвей: 
и 
. Найти их частное.
Решение
;
Очевидно, что операции умножения и деления комплексных чисел, заданных в алгебраической форме, приводит к достаточно громоздким преобразованиям, поэтому подобные операции удобнее производить с комплексными числами, заданными в показательной форме. Например, если 
, а 
то их произведение:
;
Частное от деления этих чисел:
.
Пример 6
Известны комплексные сопротивления ветвей: 
и 
. Найти их произведение и частное.
Решение
;
.