ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНИЕ
И ПОТЕНЦИАЛ
А В

В поле заряда Q поместим пробный заряд q. Под действием электрического поля Q, q начнет двигаться от точки А до бесконечности, значит электрическое поле совершает работу, то есть обладает энергией. Энергетическими характеристиками поля является потенциал и напряжение.
Электрические потенциал - это работа совершаемая силами поля по перемещению единичного заряда из одной точки поля в бесконечность.
φ - потенциал измеряется в вольтах (В)
Запишем потенциал точек А и В  ;
;  .
.
Электрическое напряжение - это работа, совершаемая силами поля по перемещению единичного заряда из одной точки поля в другую.
[U]=В  ;
;
 напряжение между двумя точками есть разность потенциалов этих точек
напряжение между двумя точками есть разность потенциалов этих точек
Потенциал Земли равен 0. 
Электрическая емкость. Конденсаторы
Энергию можно накапливать, поднимая груз (часы-ходики с кукушкой), закручивая пружину (обычные механические часы), сжимая газ (пневматическое оружие).
Энергию можно также накапливать в виде электростатического поля. Для этого служат устройства, называемые конденсаторами. В самом грубом приближении любой конденсатор - это пара проводников (обкладок), между которыми создается некая разность потенциалов Dj. Способность конденсатора накапливать энергию в форме электростатического поля характеризуется величиной его емкости. Сам этот термин восходит к временам, когда бытовало представление об электрической жидкости. Представим себе сосуд, который мы наполняем такой жидкостью. Ее уровень (перепад высот между дном сосуда и поверхностью жидкости) соответствует разности потенциалов Dj., до которой заряжается конденсатор. А количество жидкости в сосуде соответствует заряду q, сообщаемому конденсатору. В зависимости от формы сосуда при том же уровне (разности потенциалов) в него войдет больше или меньше жидкости (зарядов). Отношение

и называется емкостью конденсатора.
Уединенные проводники также обладают емкостью. Роль второй обкладки играют при этом бесконечно удаленные точки пространства. Рассмотрим, например, заряженную сферу радиусом R. Вне сферы (r>R) имеется кулоновское электрическое поле

| (2.6) |
направленное вдоль радиуса. Потенциал, создаваемый заряженной сферой при r>R, дается выражением

| (2.7) |
Внутри проводящей сферы поле отсутствует (E=0), и, следовательно, потенциал во всех точках сферы постоянен и совпадает со значением потенциала на ее поверхности

| (2.8) |
Это значение, в сущности, является разностью потенциалов между поверхностью сферы и бесконечно удаленной точкой. По определению емкость уединенной сферы будет равна

| (2.9) |
В системе СИ единицей измерения электрической емкости является фарад(Ф):
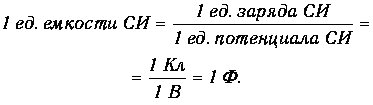
|
Фарад - это емкость такого проводника, которому для повышения потенциала на 1 В, необходимо сообщить заряд в 1 Кл.
Соотношение для емкости уединенной сферы в вакууме С=4pe0R показывает, что 1Ф - это емкость шара с радиусом R=9•109 м, что в 13 раз превышает радиус Солнца и в 1 413 раз - радиус Земли. Таким образом, емкость Земли составляет примерно 1/1413 Ф=700 мкФ. Иными словами, 1 Ф - это огромная емкость.
Плоский конденсатор. Идеальный плоский конденсатор представляет собой две металлические параллельные пластины, линейные размеры которых много больше расстояния d между ними. Пусть площадь каждой из пластин равна S (рис. 2.12).

Рис. 2.12. Электрическое поле идеального плоского конденсатора
На одну пластину помещен заряд (+q), на другую - (-q). Если пластины достаточно велики, то их можно считать «бесконечными» в том смысле, что допустимо пренебречь краевыми эффектами, то есть распределениями зарядов и конфигурациями полей вблизи их краев. Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью

Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними

| (2.10) |
Поле, создаваемое двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями, является однородным, и его напряженность равна

Напряженность поля в пространстве, окружающем пластины, можно считать равной нулю, если пренебречь краевыми эффектами. Интегрируя вдоль одной из силовых линий (которые ортогональны пластинам), получаем

| (2.11) |
Отсюда находим емкость плоского конденсатора
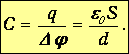
| (2.12) |
На рис. 2.13 показан опыт, в котором демонстрируется зависимость емкости раздвижного плоского конденсатора от расстояния между его пластинами. Зарядив конденсатор, присоединенный к электрометру, наблюдают уменьшение разности потенциалов между пластинами при их сближении, и увеличение - при их раздвижении. Поскольку заряд конденсатора при этом не меняется, это свидетельствует об увеличении емкости конденсатора при уменьшении расстояния между его пластинами.