Следствием этого является то, что напряжение на каждом параллельно соединённом проводнике одинаково и равно напряжению на всём участке параллельно соединённых проводников:
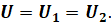
При параллельном соединении ток распределяется по проводникам так же, как поток воды, разветвляющийся на два параллельных канала. Количество воды, протекающее ежесекундно через неразветвлённую часть потока воды, равно сумме количеств воды, протекающих ежесекундно через каждый из каналов.
Аналогично обстоит дело и с прохождением электрических зарядов через параллельно соединённые проводники. Включив амперметры в цепь до разветвления и в каждую ветвь разветвления, можно убедиться, что ток в неразветвлённой части цепи равен сумме токов, текущих в отдельных параллельно соединённых проводниках:
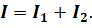
Этот опыт служит лишь подтверждением того, что в случае установившегося тока электрические заряды не скопляются в точках разветвления, а сколько их подходит к точкам разветвления, столько же и уходит.
Обозначим сопротивление каждого из разветвлённых участков цепи через R 1 и R 2, a напряжение во всей цепи через U. Теперь применим к каждой ветви закона Ома для участка цепи:
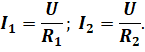
И выразим из этих формул напряжение.
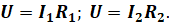
Так как напряжение на каждом параллельно соединённом проводнике одинаково, то давайте приравняем правые части последних двух равенств:
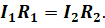
Отсюда находим, что токи в отдельных ветвях разветвлённой части цепи обратно пропорциональны их сопротивлениям:
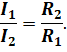
Третья закономерность параллельного соединения определяет общее сопротивление разветвлённого участка. Учтём, что сила тока в цепи равна сумме сил токов в ветвях, а напряжение везде одинаково. Тогда, на основании закона Ома, получим, что величина, обратная сопротивлению участка параллельно соединённых проводников, равна сумме величин, обратных сопротивлению отдельных проводников:
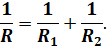
При этом общее сопротивление разветвлённой части цепи меньше наименьшего из сопротивлений её ветвей.
Нетрудно показать, что если в разветвление будет включено не два, а несколько проводников, то данная закономерность также будет выполняться:
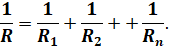
Из этого равенства следует, что общее сопротивление участка цепи, состоящего из п параллельно соединённых проводников с одинаковым сопротивлением, в п раз меньше сопротивления одного из них:
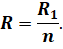
Параллельное соединение — это основной способ включения в электрическую цепь различных потребителей, так как в одну и ту же электрическую цепь могут быть включены самые различные потребители. Однако следует иметь в виду, что параллельно включаемые в данную цепь потребители должны быть рассчитаны на одно и то же напряжение, соответствующее напряжению в цепи.
Большинство задач на расчёт цепи сводится к определению токов, текущих в отдельных её участках, по заданному напряжению и по сопротивлениям отдельных проводников.
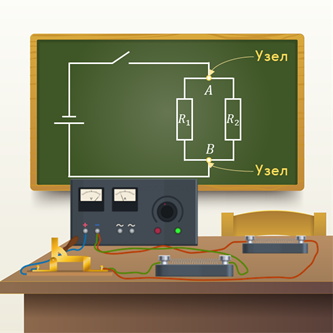
Для примера рассмотрим цепь, представленную на рисунке.
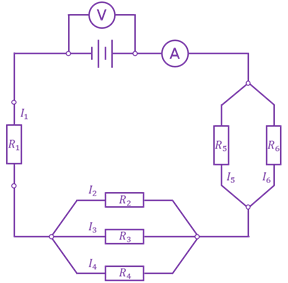
Пусть нам известно общее напряжение, питающее цепь, и сопротивления включённых в цепь резисторов (сопротивлением амперметра мы пренебрегаем, так как оно очень мало). Пусть нам надо найти силу тока, протекающего по каждому из резисторов.
Прежде всего мы должны установить, из скольких последовательных участков состоит наша цепь. Легко видеть, что таких участков три, причём второй и третий участки представляют собой разветвления. Обозначим сопротивления трёх последовательных участков нашей цепи через RI, RII, RIII.
Тогда всё сопротивление цепи выразится как сумма сопротивлений этих участков:
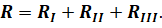
Общее сопротивление цепи необходимо знать, так как заданное общее напряжение можно отнести только к полному общему сопротивлению цепи. Применяя закон Ома, мы найдём полный ток, текущий в нашей цепи:
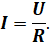
Нетрудно увидеть, что сила тока на первом резисторе равна силе тока во всей цепи:
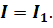
Для того чтобы найти токи в отдельных ветвях, надо предварительно найти напряжение на отдельных участках последовательных цепей. А поможет нам это сделать закон Ома:
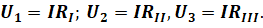
Незабываем о том, что RII и RIII — это эквивалентные сопротивления разветвлённых участков. Эти сопротивления мы с вами можем легко найти по закону параллельного соединения
Ну а дальше, зная напряжения на отдельных разветвлениях, найдём и токи в отдельных ветвях используя всё тот же закон Ома (при этом не забываем, что напряжение на концах всех параллельно соединённых проводников одно и то же):
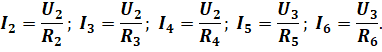
Таким образом, задача, поставленная перед нами, полностью решена.
Домашнее задание:
1. Прочитайте конспект
2. Что называется электрической цепью?
3. Что называется электрическими схемами?
4. Запишите условные знаки, которыми принято обозначать приборы на схемах
5. Запишите характеристику последовательного и параллельного соединения:
· Определение
· Постоянная величина
· Зарисуйте схему соединения
· Выпишите формулы
· Применение