Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.
В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».
В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».
В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.
В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.
Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).
Перейдем к взаимному расположению 2-х прямых в пространстве. Как и в планиметрии, две различные прямые в пространстве либо пересекаются в одной точке, либо не пересекаются (не имеют общих точек). Но второй случай допускает две возможности: прямые лежат в одной плоскости (параллельны) или прямые не лежат в одной плоскости. В первом случае они параллельны, а во втором - такие прямые называются скрещивающимися.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
|
|
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
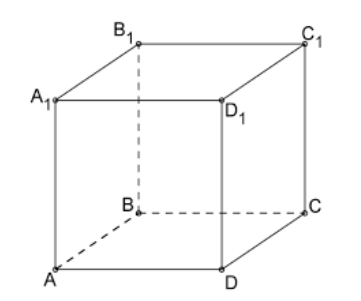Проиллюстрировать данные определения наглядно нам поможет куб.
Давайте укажем некоторые пары параллельных прямых:
AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.
А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:
AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
1. М и а задают плоскость α
2. Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. в плоскости α.
3. В плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна- это нам известно из кураса планиметрии.
4. На чертеже эта прямая обозначена буквой b.
5. Следовательно, b-единственная прямая, проходящая через точку М паралельно прямой а.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.
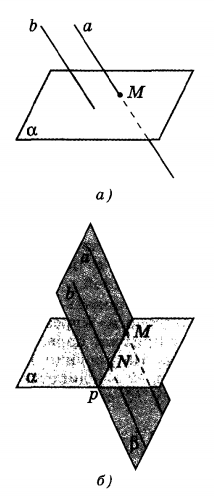Лемма. Если одна из двух паралельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
1. Рассмотрим две параллельные прямые a и b и допустим, что прямая b пересекает плоскость α в точке M(а рис.).
2. Мы знаем, что через параллельные прямые a и b можно провести только одну плоскость β. (теорема)
|
|
1. Так как точка M находится на прямой b, то M также принадлежит плоскости β (б рис.). Если у плоскостей α и β есть общая точка M, то у этих плоскостей есть общая прямая p, которая является прямой пересечения этих плоскостей (4 аксиома).
1. Прямые a, b и c находятся в плоскости β.
Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.
1. Точку пересечения прямых a и p обозначим за N.
Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.
1. Значит, прямая a пересекает плоскость α в точке N.
Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
Дано: a∥c и b∥c
Доказать: a∥b
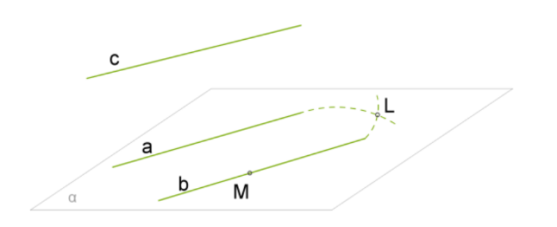Доказательство:
Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.
|
|
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:
| · 1. прямая лежит в плоскости | 
|
| · 1. прямая и плоскость имеют только одну общую точку, т.е. пересекаются |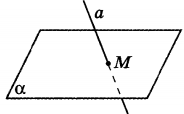 
|
| · 1. прямая и плоскость не имеют ни одной общей точки |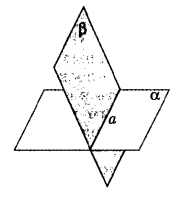 
|
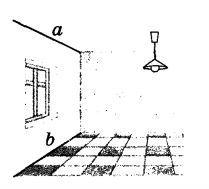
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Обозначение: a||α.
Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.
Задача 1
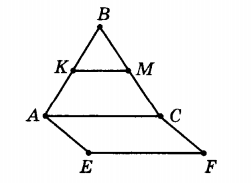
Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.
Найти: EF
Задача 2
Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.
1. АВ=2 см
2. АВ=4 см
3. АВ=5 см
4. АВ=10 см