Комбинированное занятие № 25.
Тема. Тригонометрические функции у=sin x, y=cos x, их свойства и графики.
Актуальность темы.
В рамках изучаемой темы рассматриваются основные свойства тригонометрических функций и их графики, связь данных функций с медициной и другими областями знаний, подчеркивается важность данной темы. В ходе освоения темы "Тригонометрические функции, их свойства и графики" студенты осознают роль математики и тригонометрии в медицине, а именно по расшифровке кардиограммы сердца, учатся высчитывать ЧСС (частоту сердечных сокращений), распознавать синусовый ритм (нормальный, тахикардия, брадикардия).
При изучении данной темы прослеживается связь с медициной, биологией, анатомией, что безусловно вызывает мотивацию у студентов к изучению данной темы, и позволяет в дальнейшем углубить знания по предмету.
В процессе изучения темы "Тригонометрические функции, их свойства и графики" студенты смогут в реальной жизни и в своей профессиональной деятельности определять по кардиограмме сердца ЧСС и делать заключение о характере синусового ритма.
Цель урока: Изучение тригонометрических функций, их свойств и графиков.
Определение роли тригонометрии для медицины.
Образовательные: Дать понятие тригонометрических функций у=sin x, y=cosx. Сформулировать их свойства, научится строить графики тригонометрических функций. Уметь делать заключение по кардиограмме сердца о синусоидном ритме и ЧСС.
Развивающие: Продолжить формирование умений и навыков по построению графиков, применяя зависимость y от x. Показать значимость тригонометрии для медицины.
Воспитательные: Воспитывать аккуратность, целеустремленность, дисциплинированность.Продолжить воспитание активности, взаимопомощи, творческого отношения к делу.
|
|
План занятия.
1. Актуализация знаний.
2. Изучение нового материала.
3. Закрепление изученного материала с помощью упражнений.
4. Домашнее задание. Самостоятельная работа
Ход урока.
Актуализация знаний.
Вопросы по изученным темам:
1. Что такое тригонометрические функции числового аргумента?
2.Каково значение тригонометрических функций в первой четверти
(таблица значений)?
3. Какие функции являются четными, а какие нечетными?
4.Какова симметрия графиков четных и нечетных функций?
5.Какие из тригонометрических функций являются четными (нечетными)?
Изучение нового материала
1) Начать изучение темы мне хотелось бы со слов великого математика Николая Ивановича Лобачевского:" Нет ни одной области математики, которая когда-нибудь не окажется применимой к явлениям действительного мира"
2) Поставим вопрос: Каково значение тригонометрии для медицины?
Надеюсь, после изучения нашей темы, каждый из вас сможет ответить на поставленный вопрос.
3) Итак, начнем изучение тригонометрических функций, рассмотрим их основные свойства и построим их графиики.
Тригонометрические функции.
\Посмотреть ОБЯЗАТЕЛЬНО видеоуроки:
https://youtu.be/fy2mI8MDrIo, https://youtu.be/vm7tLSCTL5M https://youtu.be/U8XQUFlufis
Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x). Рассмотрим каждую из них в отдельности.
Y = sin(x)
График функции y=sin(x).
Основные свойства:
1. Область определения вся числовая ось.
|
|
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом
равным 2π.
Y = cos(x)
График функции y=cos(x).
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом
равным 2π.
4) Зачем человеку нужно в жизни знание свойств функций и умение читать графики? Любые периодически повторяющиеся движения называются КОЛЕБАНИЯМИ
Практика изучения колебаний показала полезную и вредную роль.
Каждому специалисту необходимо владеть теорией колебательных процессов.
Теория колебаний- это область науки, связанная с математикой, физикой и медициной:
Гармонические колебания
Механические колебания
Вибрация. Вредные воздействия вибрации
Ультразвук
Инфразвукзвук
Электромагнитные колебания (применяются для радио, телевидения,
связи с космическими объектами)
Вывод:
· Колебания происходят по законам синусов и косинусов
· Свойства тригонометрических функций показывают какие параметры могут изменяться
· Результаты измерений и расчёты показывают как избежать вредных воздействий колебаний и как их применять
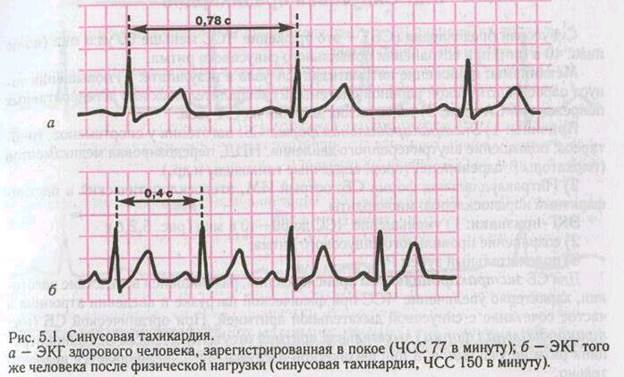
5) Остановимся подробнее, на теории колебаний в медицине. Где вы встречаетесь с колебаниями в своем организме - СЕРДЦЕ. Как называют кардиограмму сердца - СИНУСОИДА. Следовательно, сердце работает по тригонометрическим законам, и нам просто необходимо их знать и понимать.
Также тригонометрические законы встречаются и в окружающем нас мире:
|
|
- в природе (биология)
- в архитектуре (здания, сооружения)
- в музыке (гармоничные мелодии)
и в других областях.
Приложение к уроку
Рассмотреть рисунки.Обратить внимание на графики кардиограмм. Как по графику кардиограммы врач определяет отклонения в работе сердца!
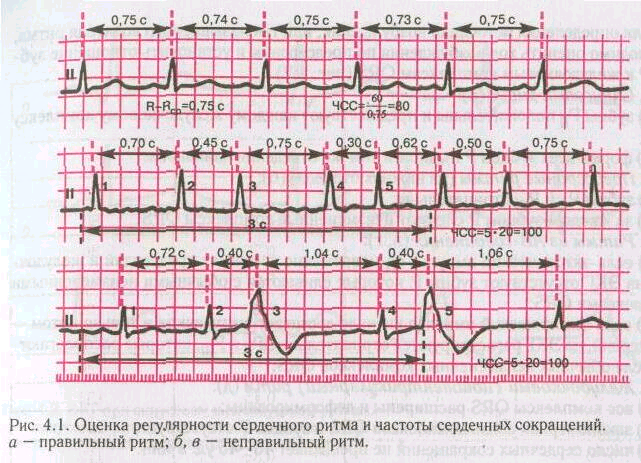
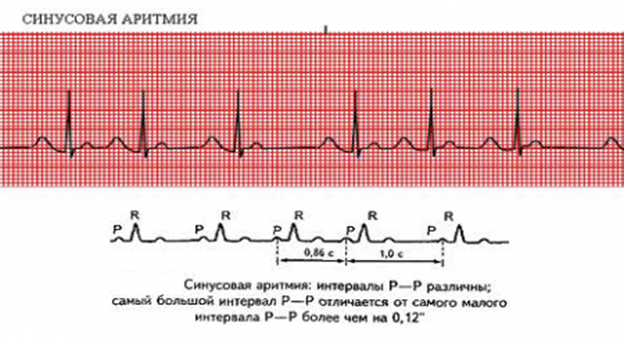
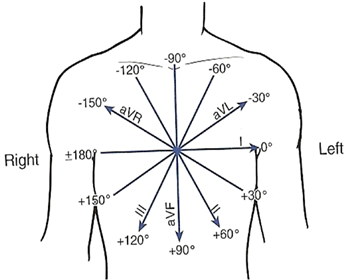
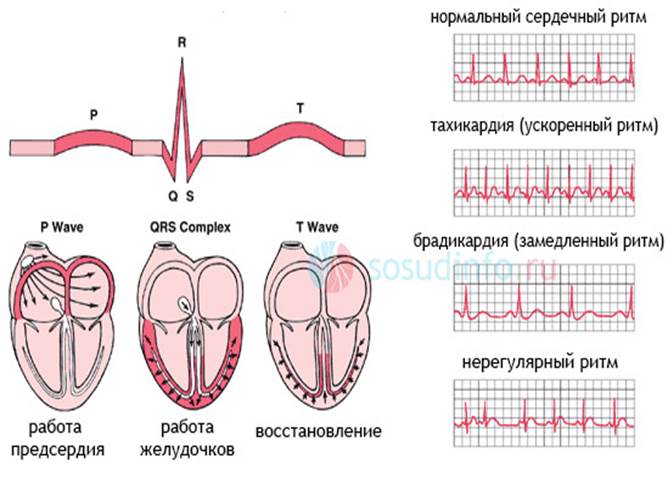
Домашнее задание:
Прочитать учебник стр.201 п.38-41, разобрать примеры из данных параграфов. сделать опорный конспект (Построить в тетради графики функций, заполнить таблицу)
Заполнить таблицу.
| Свойства функции |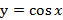 
| y =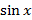 
| |
| Область определения | |||
| Область значений | |||
| Монотонность | |||
| Непрерывность | |||
| Периодичность | |||
| Чётность | |||
| Наибольшее значение ф–ии | |||
| Наименьшее значение ф-ии |
3.Выполнить упр.№ 691,692,700 (четные)
Самостоятельная работа по изученной теме:
1. Найти значение функции
y=2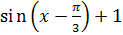 
, при x = 
.
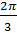2. Постройте график функции
y=2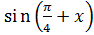 
.
3. Докажите, что функция y=f(x) является нечётной, если f(x)=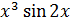 
2 
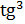x.
Список используемой литература:
Алимов Ш.А.-Алгебра и начала анализа.10-11 кл.: Учеб. для общеобразоват. учреждений. - М.: Мнемозина, 2016. - 336 с.