Функции. Общие понятия
6) Указать область определения следующих функций:
а) 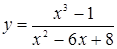 ; б)
; б) 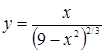
7) Найти область определения функций f и 1/f, если f задана формулой:
а) f(x)=x2 – x+1; б) f(x)=|x|-2; в) f(x)=lg(1-x2).
8) Написать формулы, задающие композиции:
а)  ; б)
; б)  ; в)
; в)  , если
, если  .
.
9) В одной системе координат построить графики функций:
а) у=х, у=х2, у=х3, у=х4; б) у=1/х, у=1/х2, у=1/х3.
10) Доказать:
а) sh(x+y)=sh x ch y +ch x sh y;
б) ch(x-y)=ch x ch y -sh x sh y.
11) Построить графики функций в полярных координатах:
а) 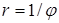 , б)
, б)  ; в)
; в) 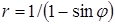
12) Построить графики уравнений, перейдя к полярным координатам:
а) 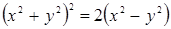 ; б)
; б)  .
.
13) В равнобедренной трапеции ABCD с основаниями AD=2, ВС=1 и высотой h=1 проведена прямая, перпендикулярная основанию AD и пересекающая его в точке М. Найти зависимость площади S отсечённой части с вершиной А от расстояния х=АМ.
14) Найти целую линейную функцию f(x)=ax+b, если f(0)=-2 и f(3)=5. Чему равны f(1) и f(2) (линейная интерполяция)?
15) Определить, какие из данных функций f(x) являются чётными, а какие нечётными:
а) 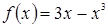 ; б)
; б) 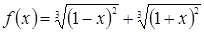 .
.
16) Функция f(x), определённая на множестве Е, называется периодической, если существует число Т>0 такое, что f(x±T)=f(x), x 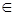 E. Выяснить, какие из данных функций являются периодическими, и определить наименьший период их, если:
E. Выяснить, какие из данных функций являются периодическими, и определить наименьший период их, если:
а)  ;
;
б)  ;
;
в)  ;
;
г) 
д) 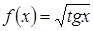
17) Температурный коэффициент линейного расширения железа а=1,2·10-6. Построить в подходящем масштабе график функции 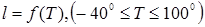 , где Т – температура в градусах и д l – длина железного стержня при температуре Т, если l=100 см при Т=00.
, где Т – температура в градусах и д l – длина железного стержня при температуре Т, если l=100 см при Т=00.
18) На числовой оси движутся две материальные точки. Первая в начальный
момент времени t=0 находилась на 20 м влево от начала координат и имела скорость v1=10 м/с; вторая при t=0 находилась на 30 м вправо от точки 0 и имела скорость v2=-20 м/с. Построить графики уравнений движений этих точек и найти время и место их встречи.
19) Газ при давлении р0 =1 кгс/м2 занимает объём v0 =12 м3. Построить график изменения объёма v газа в зависимости от давления р, если температура газа остаётся постоянной (закон Бойля-Мариотта).
20) Построить график абсолютной величины силы притяжения F материальной точки, находящейся на расстоянии х от притягивающего центра, если F=10 кгс при х=1 (закон Ньютона).
21) Согласно закону Ван-дер-Ваальса объём v реального газа и его давление р при постоянной температуре связаны соотношением  . Построить график функции р=р(v), если a=2, b=0,1 и c=10.
. Построить график функции р=р(v), если a=2, b=0,1 и c=10.
Предел функции
22) Сформулировать с помощью неравенства следующие утверждения:
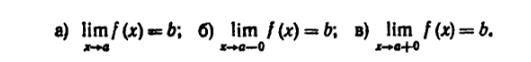
Привести соответствующие примеры.
23) Вычислить следующие пределы:
а) 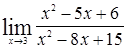 ; б)
; б) 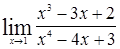 ; в)
; в)  ; г)
; г) 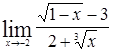 ;
;
д) 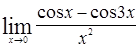 ; е)
; е) 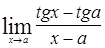 ; ё)
; ё) 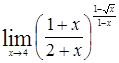 ; ж)
; ж)  ;
;
з) 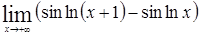 .
.
24*) Пусть х→ 1. Выделить главный член вида С(х-1)п и определить порядки малости относительно бесконечно малой х-1 следующих функций:
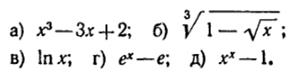
25) Определить точки разрыва и их тип у функций 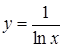 ;
;  .
.
26) Является ли непрерывной функция

27) При каком значении числа а функция f(x) будет непрерывной?
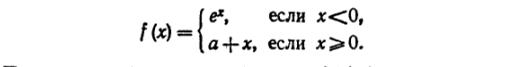
28) Определить однозначные непрерывные ветви обратных функций для следующих функций:
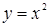 ; у=2х – х2; у=2х/(1+х2); y=sinx; y=cosx; y=tgx.
; у=2х – х2; у=2х/(1+х2); y=sinx; y=cosx; y=tgx.
29*) Доказать равенства:
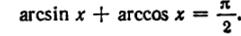


где ε – функция, принимающая одно из трёх значений: 0, 1, -1.
Дифференцирование функций
30) Определить приращение Δх аргумента х и соответствующее приращение Δу функции у=lgx, если х изменяется от 1 до 1000;
31) Определить приращение Δх аргумента х и соответствующее приращение Δу функции у=1/х2, если х изменяется от 1 до 1000.
32) Закон движения точки по оси Ох даётся формулой х=10t+5t2, t – время в секундах и х – расстояние в метрах. Найти среднюю скорость движения за промежуток времени 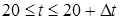 и произвести численный расчёт, если: а) Δt=1; б) Δt=0,1; в) Δt=0,01. Чему равна скорость движения в момент времени t=20 с?
и произвести численный расчёт, если: а) Δt=1; б) Δt=0,1; в) Δt=0,01. Чему равна скорость движения в момент времени t=20 с?
33) (любые 3) Найти производные следующих функций:

| 
| 
| 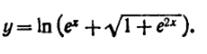
|
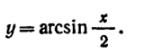
| 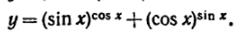
|
34) Производная от логарифма данной функции y=f(x) называется логарифмической производной этой функции:

Найти логарифмическую производную от функции у, если:

35*) Вывести формулу для сумм:

36) С какой скоростью изменяются площадь и диагональ прямоугольника, когда одна сторона его х=20 см, а другая сторона у=15 см, если первая сторона прямоугольника уменьшается со скоростью 1 м/с, а вторая возрастает со скоростью 2 м/с?
37) (любые 2) Найти производные 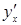 (параметры положительны:)
(параметры положительны:)

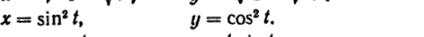


38) (любые 2) Найти производную 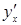 от функций, заданных неявно:
от функций, заданных неявно:

39) (любые 2) Найти 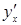 , если:
, если:

40) В каких точках кривой у=2+х-х2 касательная к ней а) параллельна оси Ох; б) параллельна биссектрисе первого координатного угла?
41*) Определить угол между левой и правой касательными к кривой:
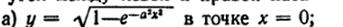
42) Найти дифференциал функции у, если:
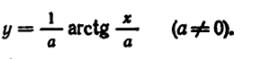
43) Найти:
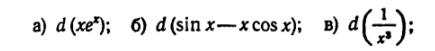
44) (любое) Заменяя приращение функции дифференциалом, найти приближённо следующие значения:
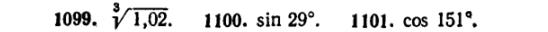
45) (любые 2) Доказать приближённую формулу:

и с помощью неё приближённо вычислить:
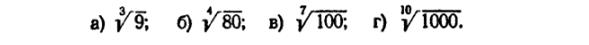
46) (любые 2) Пусть u, v, w – дифференцируемые от х функции. Найти дифференциал функции у, если:
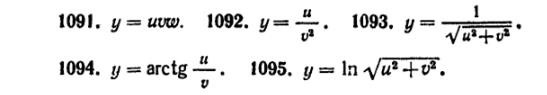
47) (любые 2) Найти у”, если:
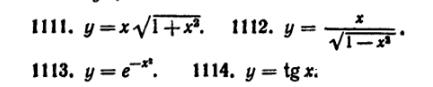
48) Найти у(0), у’(0), y”(0), если
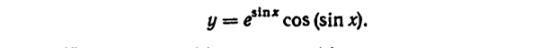
49) (любые 2) Пусть u и v – дважды дифференцируемые функции от переменной х. Найти дифференциал второго порядка, если:
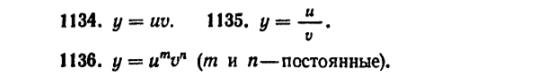
50) (любые 2) Найти производные первого, второго и третьего порядков от функции у=у(х), заданной параметрически:

51) Найти производные первого, второго и третьего порядков в точке М от функции у=у(х), заданной неявно:
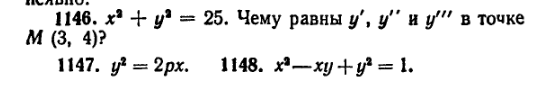
52) (любые 2) Найти производные указанного порядка:

53) (любое) Считая х независимой переменной, найти дифференциалы указанного порядка:

54) (любые 2) Разложить указанную функцию в ряд Тейлора вблизи 0 с указанной точностью:
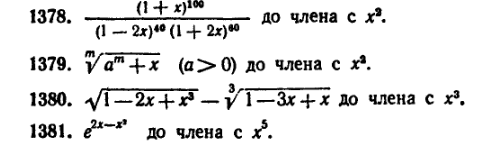
55) (любые 4) С помощью формулы Тейлора приближённо вычислить:

56) (любые 5) Провести исследование и построить графики следующих функций:
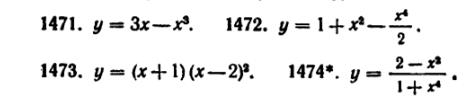
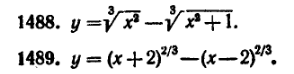

57) (любые 4) Решить следующие задачи:


58) (любые 2) Решить приближённо уравнения: