Тема 13. Энергетический метод определения перемещений. Теорема Кастилиано. Интегралы Мора
Потенциальная энергия в общем случае нагружения
Для решения задач с использованием энергетического метода определения перемещений необходимо уметь определять потенциальную энергию деформации в общем случае нагружения, когда в сечении одновременно действуют все шесть внутренних силовых факторов. Формулы для определения потенциальной энергии в частных случаях нагружения (растяжение – сжатие, сдвиг, кручение, поперечный изгиб) известны из предыдущей части курса. Рассмотрим общий случай нагружения и выделим элемент бруса длиной dz (рис. 13.1).
| dz |
| N |
| Qx |
| Qy |
| Мy |
| Мk |
| y |
| О |
| x |
| z |
| Мx |
Рис. 13.1. Общий случай нагружения бруса
В каждом из поперечных сечений бруса возникают шесть внутренних силовых факторов, которые по отношению к выделенному элементу бруса можно рассматривать как внешние. При деформации выделенного элемента эти силовые факторы совершают работу, которая переходит в потенциальную энергию деформации. Определим эту работу.
Условно будем считать левое сечение неподвижным, так что работа всех силовых факторов, действующих в этом сечении равна нулю (нет перемещений). Центр тяжести правого сечения получит некоторое малое линейное перемещение, а само сечение повернется на некоторый угол относительно осей Ox, Oy и Oz. При этом каждый из силовых факторов, приложенных к правому сечению, совершает работу на перемещении, на котором остальные пять силовых факторов работы не совершают. Например, при повороте сечения относительно оси Oz работу совершает только крутящий момент Мк. На перемещении вдоль оси Oz работу совершает только нормальная сила N и т.д.
Из указанного следует, что потенциальная энергия выделенного элемента будет равна сумме независимых работ всех шести силовых факторов на соответствующих обобщенных перемещениях. Зная выражения для потенциальной энергии от действия каждого внутреннего силового фактора, получим
(13.1)
Слагаемые в выражении (13.1) вычисляются на каждом характерном участке, где действует соответствующий силовой фактор. В большинстве практически значимых случаев последние три слагаемых существенно меньше трех первых и ими обычно пренебрегают.
Теорема Кастилиано
Элементы конструкции ЛА должны быть не только прочными, но и достаточно жесткими, т.е. максимальные эксплуатационные деформации не должны превышать некоторых заданных значений. Так, для валов ограничивают погонный угол закручивания, для балок (например, лопастей несущего винта вертолета) – максимальные прогибы и т.д. Методы вычисления деформаций прямого бруса при различных частных случаях нагружения (растяжение – сжатие, поперечный изгиб, кручение) рассмотрены в предыдущих темах дисциплины.
Аналитические методы расчета деформаций элементов конструкции используются не только при решении задач жесткости. На их основе разработаны общие методы расчетов статически неопределимых систем, а также целого ряда динамических задач сопротивления материалов, о чем будет сказано далее.
Методы определения перемещений в общем случае нагружения чаще всего основываются на общих энергетических теоремах сопротивления материалов и, в частности, на теореме Кастилиано для линейных упругих систем. Теорема формулируется следующим образом:
Частная производная от потенциальной энергии системы по силе равна перемещению точки приложения силы по направлению ее действия.
Докажем эту теорему.
Рассмотрим произвольное тело, нагруженное некоторой системой статически уравновешенных сил и моментом (рис. 13.2). Предположим, что под действием этой системы внешних (обобщенных) сил в теле накоплена потенциальная энергия U.
| P1 |
| P2 |
| Pn+dPn |
| M1 |
Рис. 13.2. К выводы теоремы Кастилиано
При увеличении одной из действующих сил, например Pn, на величину dPn потенциальная энергия системы в целом увеличится на 
и будет равна
(13.2)
Изменим порядок приложения сил. Сначала приложим силу dPn. Точка приложения этой силы получит малое перемещение, проекцию которого на направление действия силы dPn обозначим dδn. Потенциальная энергия деформации будет равна работе силы dPn на соответствующем перемещении dδn, т.е. 
(1/2 – т.к. перемещением зависит от силы). Затем приложим исходную систему сил. При отсутствии силы dPn потенциальная энергия системы была бы равна U, но при наличии силы dPn потенциальная энергия тела дополнительно возрастает на величину работы, которую совершит сила dPn на перемещении δn, вызванном всей системой внешних сил. Так как сила dPn на перемещении δn не изменяется по величине, то ее работа на данном перемещении уже будет равна dPn δn, где δn – проекция полного перемещения точки приложения силы Pn на направление ее действия.
Таким образом, при изменении порядка приложения сил суммарная потенциальная энергия деформации системы будет равна
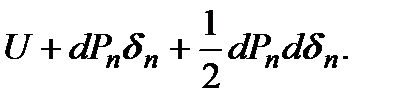(13.3)
На основании принципа независимости действия сил можно утверждать, что суммарная потенциальная энергия в теле, накопленная при действии некоторой системы внешних сил, не зависит от последовательности их приложения. Значит выражения (13.2) и (13.3) можно приравнять. Пренебрегая слагаемым 
, как величиной второго порядка малости имеем
(13.4)
Зависимость (13.4) и является математической формулировкой теоремы Кастилиано.
В формуле (13.4) силу Pn следует трактовать как обобщенную силу, т.е. как некоторый силовой фактор, а величину δn как обобщенное перемещение, представляющее собой некоторый геометрический параметр, на котором обобщенная сила совершает работу. Например, действие пары сил на тело можно задать моментом М, тогда работа этой пары сил определяется произведением этого момента на соответствующее обобщенное перемещение Мφ, где φ – угловое перемещение тела в точке приложения момента и в направлении его действия.
Для балки, нагруженной равномерно распределенной нагрузкой q и прогиб которой определяется функцией y(z), работа распределенной нагрузки будет равна
,
где q – обобщенная сила, а обобщенным перемещением является площадь ω, заключенная между осью балки в недеформированном состоянии и ее изогнутой осью после деформации.
Теорему Кастилиано в рассмотренном виде можно использовать лишь для тех систем, для которых справедлив принцип независимости действия сил и принцип начальных размеров. В случае нелинейной зависимости между силами и перемещениями теорему Кастилиано следует записывать в более общем виде, тогда ее рассмотренная трактовка будет являться частным случаем обобщенных соотношений.
Поясним порядок определения перемещений с использованием теоремы Кастилиано на простейших примерах.
Пример 1. Определить перемещение правого торца стержня, нагруженного продольной силой Р (рис. 13.3а). Принять жесткость стержня EF=const.
| A |
| z |
| l |
| P |
| a) |
| l |
| P |
| б) |
Рис. 13.3. Перемещение стержня от действия продольной силы Р
Решение:
1. При заданной нагрузке в поперечных сечениях стержня будет действовать лишь один внутренний силовой фактор – поперечная сила N=P, т.е. имеет место простое растяжение. Потенциальная энергия деформации при растяжении равна
2. Дифференцируя выражение для потенциальной энергии по силе Р, находим перемещение точки приложения силы в направлении ее действия (13.4)
.
Полученное выражение совпадает с результатом вычисления перемещений стержня при растяжении – сжатии.
Пример 2. Определить прогиб балки в точке А (рис. 13.3б), нагруженной сосредоточенной силой Р.
Решение:
1. В поперечном сечении балки возникают два внутренних силовых фактора: поперечная сила Q=P и изгибающий момент M(z), т.е. имеет место поперечный изгиб. Будем считать, что вкладом поперечной силы в прогиб балки можно пренебречь. Изгибающий момент в текущем сечении z определяется известным соотношением M(z)=-Pz. Тогда можно записать формулу для вычисления потенциальной энергии при изгибе
2. Дифференцируя полученное выражение по силе Р, находим искомый прогиб в точке А по направлению действия силы Р
Полученный результат совпадает с решением, полученным ранее путем интегрирования приближенного дифференциального уравнения упругой линии балки.
Интеграл Мора
Теорема Кастилиано позволяет определить перемещения только тех точек и сечений произвольного тела, в которых приложены внешние обобщенные силы и только в направлении их действия. Однако на основе этой теоремы могут быть получены зависимости, позволяющие определять обобщенные перемещения любых точек и сечений рассматриваемого тела в произвольных направлениях.
Рассмотрим пространственную стержневую конструкцию, нагруженную произвольной системой внешних сил (рис. 13.4)
| P3 |
| Ф |
| C |
| M1 |
| P1 |
| P2 |
| x1 |
Рис.13.4. Стержневая система под действием произвольной системы внешних сил
Предположим, что требуется определить перемещение точки С в направлении x1. Приложим в точке С в направлении x1 обобщенную силу Ф. Внутренние силовые факторы в произвольном сечении представим в виде:
(13.5)
В данных соотношениях Mkp, Mxp,…, Np – внутренние силовые факторы в рассматриваемом сечении при действии заданной системы внешних сил. Вторые слагаемые представляют собой приращения интегральных внутренних силовых факторов, возникающие при приложении силы Ф. Очевидно, что значения дополнительных силовых факторов будет пропорционально силе Ф, причем Mk1, Mx1,…, N1 – коэффициенты пропорциональности, зависящие от положения рассматриваемого сечения. Если снять систему внешних сил (Mkp, Mxp,…, Np – равны нулю) и заменить силу Ф единичной силой, то, как следует из записанных равенств, коэффициент пропорциональности представляет собой внутренние силовые факторы, возникающие в рассматриваемом сечении под действием единичной силы, приложенной в рассматриваемой точке в заданном направлении.
Запишем общее выражение для потенциальной энергии деформации (13.1) с учетом реально действующей системы сил (13.5)
Возведем выражение в скобках для каждого слагаемого в квадрат, продифференцируем по силе Ф и положим, что эта сила равна нулю, т.е. Ф=0.
В качестве примера приведем алгоритм вычислений при учете лишь одного силового фактора – крутящего момента 
.
(13.6)
Для определения обобщенного перемещения в точке приложения обобщенной силы 
в направлении ее действия дифференцируем выражение (13.6) по силе 
:
. (13.7)
Положим, что сила равна нулю и окончательно получим обобщенное перемещение в точке С, вызванное действием крутящего момента
(13.8)
Очевидно, что по аналогии при учете всех шести внутренних силовых факторов можно получить обобщенное перемещение точки С в направлении действия обобщенной силы Ф:
(13.9)
Полученные интегралы называют интегралами Мора. При выводе зависимости (13.9), как и отмечалось ранее при рассмотрении теоремы Кастилиано, под δС следует понимать обобщенное перемещение, а Ф – обобщенная сила. Так, если требуется найти линейное перемещение точки С в направлении x1 (рис.13.4), то при составлении функциональных выражений для Mk1, Mx1,…, N1 необходимо в этой точке приложить единичную силу в направлении x1. Если требуется найти угловое перемещение относительно некоторой оси, то следует приложить единичный момент в соответствующей плоскости относительно этой оси.
Следует отметить, что при практических расчетах учитывают, что первые (моментные) три слагаемых в выражении (13.9) существенно больше трех остальных (силовых), что позволяет обычно последними слагаемыми пренебречь.
Если стержневая система включает прямые участки с постоянной жесткостью, то вычисление интегралов вида (13.9) можно упростить, учитывая линейный характер эпюр внутренних силовых факторов на этих участках. Поясним возможный алгоритм вычисления подобных интегралов при практических расчетах.
Пусть требуется вычислить интеграл от произведения двух функций – произвольной y1=f1(z) и линейной y2=d+kz (рис. 13.5) на участке длиной b-а.
| f2(zцт) |
| zцт |
| b |
| C |
| dz |
| z |
| O |
| O |
| y |
| y |
| z |
| z |
| a |
| Ω |
| y1=f1(z) |
| y2=d+kz |
Рис.13.5. Вычисление интеграла Мора
Проведем преобразования
(13.10)
Первый интеграл в полученном выражении представляет собой площадь Ω, ограниченную кривой y1=f1(z), т.е. его можно записать в виде
Второе интеграл представляет собой статический момент площади, ограниченной кривой y1=f1(z) на участке ab, относительно оси Oy, т.е.
.
Итого исходный интеграл (13.10) можно записать в виде
(13.11)
Таким образом, искомый интеграл равен произведению площади первой (нелинейной) эпюры на ординату линейной эпюры под центром тяжести первой. Если обе эпюры линейны, то операция перемножения эпюр обладает свойством коммутативности. В сопротивлении материалов такая операция по вычислению интеграла Мора путем перемножения эпюр двух функций носит название – правило Верещагина.
Проверку на жесткость проводят после подбора поперечных сечений, когда эпюры внутренних силовых факторов во всех элементах конструкции построены (известны). Во многих случаях эти эпюры могут быть разбиты на простейшие фигуры, для которых значение площади Ω и положение центра тяжести этой площади известны (прямоугольник, треугольник и др.). В этом случае операция интегрирования может быть заменена рассмотренным графоаналитическим методом.
Поясним порядок вычисления обобщенных перемещений в упругой системе с использование интеграла Мора и правила Верещагина.
Пример. Пусть дана консольная балка длиной l, нагруженная сосредоточенной силой P, как показано на рис. 13.6. Требуется определить угол поворота сечения в точке С. Будем считать, что балка постоянного поперечного сечения и ее изгибная жесткость 
Влиянием поперечных сил на обобщенные перемещения системы пренебречь.
Решение задачи с использованием интеграла Мора.
Эпюра изгибающего момента от силы Р по длине балки описывается уравнением
Эпюра изгибающего момента от действия единичного изгибающего момента, приложенного в точке С, описывается соотношением
Тогда обобщенное перемещение (угол поворота сечения) в точке С можно определить, используя интеграл Мора
Знак (-) в полученном выражении говорит о том, что поперечное сечение балки повернется на угол в направлении, противоположном приложенному единичному моменту.
|
| z |
|
| l/2 |
|
| С |
| z |
|
| P |
| y |
| l/2 |
| z |
| z |
|
Рис. 13.6. Вычисление угла поворота сечения для консольной балки
Решение задачи с использованием правила Верещагина.
В этом случае для балки постоянного поперечного сечения можно воспользоваться соотношением вида (13.11)
где 
- площадь первой эпюры на участке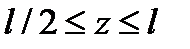 
(Внимание! При вычислении площади ординаты берутся со своим знаком);
- ордината на второй эпюре под центром тяжести первой. Итого имеем
Знак (-) в полученном выражении говорит о том, что поперечное сечение балки повернется на угол в направлении, противоположном приложенному единичному моменту, т.е. направление действия единичного момента было выбрано неверно.