Транспортная задача
Лекция 5-6
Постановка транспортной задачи
Имеется 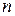 поставщиков
поставщиков 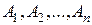 , у которых сосредоточены запасы однородного груза в количестве
, у которых сосредоточены запасы однородного груза в количестве 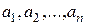 единиц соответственно. Этот груз нужно доставить
единиц соответственно. Этот груз нужно доставить 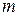 потребителям
потребителям 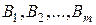 , заказавшим
, заказавшим 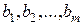 единиц этого груза. Также известны тарифы на перевозку груза
единиц этого груза. Также известны тарифы на перевозку груза 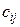 (стоимость доставки единицы продукции) от
(стоимость доставки единицы продукции) от  -го поставщика к
-го поставщика к 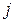 -му потребителю. Необходимо составить план перевозок, при котором запасы всех поставщиков реализованы, спрос потребителей удовлетворен, а общая стоимость перевозок минимальна.
-му потребителю. Необходимо составить план перевозок, при котором запасы всех поставщиков реализованы, спрос потребителей удовлетворен, а общая стоимость перевозок минимальна.
Условие транспортной задачи удобно записать в виде таблицы.
Таблица 3.1. Транспортная таблица
| Поставщики | Потребители | Запасы | |||
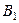
| 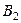
| 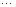
| 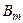
| ||
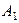
| 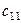
| 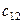
| 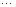
| 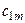
| 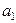
|
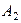
| 
| 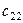
| 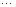
| 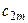
| 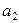
|
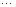
| 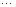
| 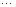
| 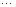
| 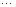
| 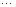
|
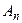
| 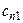
| 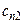
| 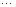
| 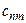
| 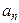
|
| Потребности | 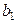
| 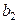
| 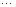
| 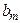
|
Неизвестные переменные транспортной задачи – объемы перевозок 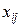 от
от  -го поставщика
-го поставщика 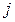 -му потребителю,
-му потребителю, 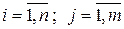 . Эти переменные записываются в виде матрицы перевозок:
. Эти переменные записываются в виде матрицы перевозок:
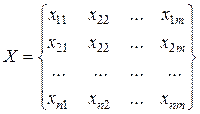 .
.
Математическая постановка транспортной задачи:
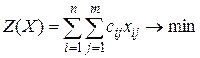 , (3.1) , (3.1)
| 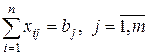 , (3.2) , (3.2)
|
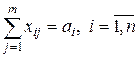 , (3.3) , (3.3)
| 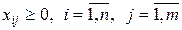 . (3.4) . (3.4)
|
Опорный план – всякое неотрицательное решение системы (3.2)-(3.4), определяемое матрицей 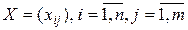 .
.
Оптимальный план – план 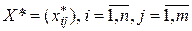 , при котором целевая функция
, при котором целевая функция 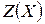 принимает свое минимальное значение.
принимает свое минимальное значение.
Необходимое и достаточное условие разрешимости транспортной задачи
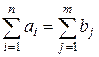 . (3.5)
. (3.5)
Если условие (3.5) выполняется, задача называется сбалансированной, модель – закрытой. Если условие (3.5) не выполняется, то задача – несбалансированная, модель – открытая.
Если задача является открытой, то необходимо свести ее к закрытому типу. Если 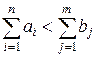 , добавляется фиктивный поставщик
, добавляется фиктивный поставщик 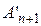 с запасом груза
с запасом груза 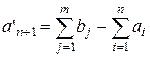 . Если
. Если 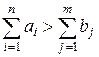 , то добавляется фиктивный потребитель
, то добавляется фиктивный потребитель 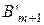 с потребностью
с потребностью 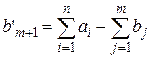 . Соответствующие фиктивным объектам тарифы перевозок
. Соответствующие фиктивным объектам тарифы перевозок 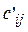 полагаем равными нулю, чтобы суммарная стоимость перевозок
полагаем равными нулю, чтобы суммарная стоимость перевозок 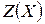 не изменялась.
не изменялась.
Цель решения транспортной задачи – определение переменных 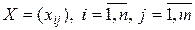 , при которых выполняются ограничения (3.2)-(3.4), и целевая функция (3.1) принимает минимальное значение.
, при которых выполняются ограничения (3.2)-(3.4), и целевая функция (3.1) принимает минимальное значение.
Алгоритм решения транспортной задачи:
1. Построение первоначального плана перевозок (метод северо-западного угла, метод минимальной стоимости);
2. Оптимизация плана (метод потенциалов).
Метод северо-западного угла
Составление плана перевозок начинается с распределения запасов товара поставщика 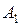 . Будем за счет его запасов удовлетворять заказы потребителя
. Будем за счет его запасов удовлетворять заказы потребителя  , затем
, затем 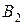 и т.д. Таким образом, будем заполнять таблицу, начиная с клетки (1, 1), и двигаться вправо по строке до тех пор, пока остаток запасов поставщика
и т.д. Таким образом, будем заполнять таблицу, начиная с клетки (1, 1), и двигаться вправо по строке до тех пор, пока остаток запасов поставщика 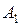 не окажется меньше заказа очередного потребителя. Далее аналогичным образом распределим запасы поставщика
не окажется меньше заказа очередного потребителя. Далее аналогичным образом распределим запасы поставщика  , затем
, затем 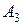 и т.д.
и т.д.
Пример 1. Предположим, что имеются поставщики 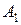 ,
, 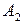 и
и 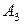 ресурса, потребителями которого являются предприятия
ресурса, потребителями которого являются предприятия 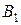 ,
, 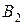 ,
, 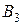 и
и 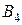 .
.
В условии задачи известны количества ресурсов 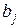 , необходимые предприятиям; возможности поставщиков
, необходимые предприятиям; возможности поставщиков 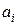 , а также тариф на доставку единицы ресурса от
, а также тариф на доставку единицы ресурса от  поставщика к
поставщика к 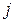 потребителю
потребителю  . Начальные данные приведены в табл. 3.2.
. Начальные данные приведены в табл. 3.2.
Таблица 3.2 – Транспортная таблица с исходными данными
| Поставщики | Потребители | Запасы | |||
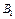
| 
| 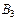
| 
| ||
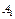
| |||||
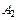
| |||||
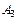
| |||||
| Потребности |
Необходимо построить первоначальный план снабжения методом северо-западного угла.
Решение.
Из табл. 3.2 видно, что транспортная задача сбалансированая.
Шаг № 1. Северо-западный угол табл. 3.2 – клетка (1, 1). У поставщика 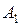 есть 160, а потребителю
есть 160, а потребителю  нужно 100 единиц товара. Находим минимум из этих двух чисел: min (160, 100) = 100. Клетка (1, 1) перечеркивается по диагонали сплошной чертой (––––), в правом нижнем углу пишется найденный минимум. Это означает, что поставщик
нужно 100 единиц товара. Находим минимум из этих двух чисел: min (160, 100) = 100. Клетка (1, 1) перечеркивается по диагонали сплошной чертой (––––), в правом нижнем углу пишется найденный минимум. Это означает, что поставщик 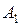 должен отправить потребителю
должен отправить потребителю  100 единиц товара. Такие клетки в дальнейшем будем называть отмеченными.
100 единиц товара. Такие клетки в дальнейшем будем называть отмеченными.
Так как потребность потребителя  полностью удовлетворена, то данный потребитель исключается из рассмотрения. Поэтому все остальные клетки 1-го столбца закрашиваются. Они называются пустыми и в дальнейшем исключаются из рассмотрения.
полностью удовлетворена, то данный потребитель исключается из рассмотрения. Поэтому все остальные клетки 1-го столбца закрашиваются. Они называются пустыми и в дальнейшем исключаются из рассмотрения.
Таблица. 3.3 – Транспортная таблица, полученная на шаге № 1
| Поставщики | Потребители | Запасы | |||
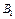
| 
| 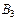
| 
| ||
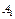
| |||||
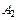
| |||||
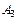
| |||||
| Потребности |
Первый столбец в дальнейшем не рассматривается.
Шаг № 2. Северо-западный угол табл. 3.3 – клетка (1, 2). Поэтому рассмотрим 1-го поставщика и 2-го потребителя. Оставшаяся мощность (объем запаса) поставщика 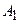 равна 60. Спрос потребителя
равна 60. Спрос потребителя 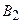 – 40. Находим минимум min (60, 40) = 40. Клетка (1, 2) становится отмеченной.
– 40. Находим минимум min (60, 40) = 40. Клетка (1, 2) становится отмеченной.
Таблица 3.4 – Транспортная таблица, полученная на шаге № 2
| Поставщики | Потребители | Запасы | |||
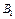
| 
| 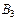
| 
| ||
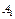
| |||||
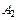
| |||||
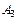
| |||||
| Потребности |
Шаг № 3. Северо-западный угол табл. 3.4 – клетка (1, 3): min (20, 80) = 20.
Таблица 3.5 – Транспортная таблица, полученная на шаге № 3
| Поставщики | Потребители | Запасы | |||
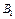
| 
| 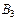
| 
| ||
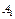
| |||||
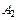
| |||||
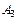
| |||||
| Потребности |
Шаг № 4. Северо-западный угол табл. 3.5 – клетка (2, 3): min (30, 60) = 30.
Таблица 3.6 – Транспортная таблица, полученная на шаге № 4
| Поставщики | Потребители | Запасы | |||
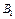
| 
| 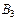
| 
| ||
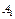
| |||||
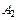
| |||||
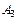
| |||||
| Потребности |
Шаг № 5. Северо-западный угол табл. 3.6 – клетка (3, 3): min (90, 30) = 30.
Таблица 3.7 – Транспортная таблица, полученная на шаге № 5
| Поставщики | Потребители | Запасы | |||
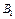
| 
| 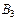
| 
| ||
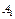
| |||||
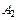
| |||||
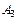
| |||||
| Потребности |
Шаг № 6. В табл. 3.7 осталась незаполненная клетка (3, 4): min (90‑30, 60)=60.
Таблица 3.8 – Транспортная таблица, полученная на шаге № 6
| Поставщики | Потребители | Запасы | |||
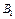
| 
| 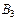
| 
| ||
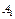
| |||||
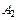
| |||||
| |||||
| Потребности |
Общая стоимость всех перевозок по полученному опорному плану:
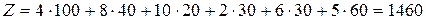 .
.