1. Длина деления шкалы – расстояние между осями (или центрами) двух соседних отметок шкалы, измеренное вдоль воображаемой линии, проходящей через середины самых коротких отметок шкалы. Деления шкал относятся к штриховым мерам длины, поэтому каждый штрих, даже нанесённый очень тщательно, имеет ограниченную толщину. Эта толщина вносит ошибку в процесс измерения. Для компенсации этой ошибки за номинальное расположение деления принята его середина. Для круговых шкал середина деления лежит на воображаемой окружности имеющей радиус средний между наибольшим и наименьшим радиусами расположения всех делений шкалы. Штрих, проставленный на шкале (по РМГ-29-99) называется отметкой шкалы. Число, проставленное около этой отметки, называется числовой отметкой.
2. Цена деления шкалы – разность значений соответствующих двум соседним отметкам шкалы, выраженная в единицах измеряемой величины.
D = b – a

3. Длина шкалы – длина линии, проходящей через центры всех самых коротких отметок шкалы, и ограниченная начальной и конечной отметками.
4. Начальное значение шкалы – наименьшее значение, которое может быть отсчитано по шкале СИ.
5. Конечное значение шкалы – наибольшее значение измеряемой величины, которое может быть отсчитано по шкале. Заметим здесь, что отсчитано не означает измерено, ибо прибор может позволять измерять большие величины, чем обеспечивает генератор данных величин. Например, спидометр изготовляют всегда с запасом, т.е. конечное значение величины всегда больше предельной скорости автомобиля, которую может обеспечить двигатель.
6. Метрологическая характеристика СИ – характеристика, влияющая на результат измерений и его погрешность.
7. Показание средства измерения.
8. Вариация показаний измерительного прибора – разность показаний при подходе к одной точке справа и слева.
9. Диапазон показаний СИ – область значений шкалы, ограниченная начальным и конечным значениями шкалы, т.е. наибольшим и наименьшим значениями измеряемой величины, регистрируемой только по шкале измерений.
10. Диапазон измерений СИ – область значений величины, в которой нормированы допускаемые погрешности СИ. Например, диапазон показаний спидометра автомобиля начинается с нуля, но измерена скорость с нормированной постоянной точностью может быть только с некоторых реальных значений.

11. Влияющая физическая величина.
12. Нормальные рабочие условия. (самостоятельно).
13. Чувствительность измерительного прибора – отношение сигнала на выходе к изменению сигнала физической величины.
14. Порог чувствительности. (самостоятельно).
15. Градуировочная характеристика СИ – зависимость между значениями величин на входе и выходе СИ полученная экспериментально, выраженная в виде формулы, графика или таблицы.
Шкалы

Шкала наименований – когда объекты шкалы отмечаются числом или другим условным знаком.


Шкала порядка (рангов) – когда объекты шкалы выстраиваются по возрастанию или убыванию количественного проявления свойств. Например, шкала твёрдости Мооса:

Погоны по родам войск – шкала наименований, а по званиям – шкала рангов.
Шкала интервалов (разностей) - такая шкала состоит из одинаковых интервалов, линейна и имеет единицу измерения. Ноль в такой шкале принимается по соглашению. Например, летоисчисление от Новой эры (от Рождества Христова) или от Сотворения мира. На Руси раньше считали года от мифической даты “от сотворения мира”, которая якобы была в 5508 году до Рождества Христова. С 1 января 1700 года по указу Петра Великого в России считают годы от Р.Х. или от Новой эры. Существуют и другие системы счёта лет. Например, мусульмане считают годы от Хиджры – переселения пророка Мухаммеда из Мекки в Медину, которое согласно легенде произошло в 583 году н. э. Также температурные шкалы Цельсия, Фаренгейта, Реомюра.

Температурная шкала Цельсия
Все эти шкалы за опорные точки принимают точку кипения воды и точку таяния льда. Только шкала Цельсия разделена на 100 частей, Фаренгейта на 212 (причём точка кипения воды считается 212 градусов, а таяния льда 32 градуса), а Реомюра на 80 (где точка таяния льда считается за 0 градусов, а кипения воды за 80).


Шкала звёздных величин см. сайт кафедры.
Шкала отношений – наиболее совершенная из всех шкал, применяемых для измерения физических величин. Для таких шкал действует основное уравнение измерения:

где q – число единиц, а U – величина единицы измерения. С помощью таких шкал измеряется длина, масса, сила тока и т.д.
Определение измерения: Измерить какую-либо величину – значит опытным путём найти её отношение к соответствующей единице измерения.: https://www.znaytovar.ru/new2619.html


Погрешности измерений.
Результат измерения — значение величины, полученное путём её измерения. Он представляет собой приближённую оценку истинного значения величины.
Погрешность результата измерений – отклонение результата измерения от истинного (действительного) значения измеряемой величины. Xизм – результат измерения, Xист = Xд = X – истинное или действительное значение. Погрешность:
DX = Xизм – Xд
Это абсолютная погрешность измерений. Относительная погрешность:
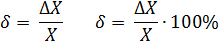
Точность измерений – качество измерений, отражающее близость их результатов к истинному значению измеряемой величины, равна обратной величине модуля относительной погрешности:

Допускаемая погрешность зависит от требуемой точности измерений и установлена ГОСТом. Предельно допустимая погрешность зависит от допуска размера и принимается равной [d] = (0.2…0.3)Td. Каждое средство измерения характеризуется основной погрешностью, которое указано а паспорте на это СИ.
Рассеяние результатов в ряду измерений.
Размах результатов измерений: R = Xmax – Xmin.
Среднее квадратическое отклонение (СКО):
xi – i-й результата измерений, xср – среднее арифметическое значение из n единичных результатов, которое равно:
Средняя квадратическая погрешность результатов измерения среднего арифметического (СКП):

Если результаты свободны от систематических погрешностей, то СКП и СКО одинаковы.
Систематическая погрешность измерения – составляющая погрешности, остающаяся неизменной или изменяющаяся по определённому закону. Систематические погрешности бывают постоянные, прогрессивные и изменяющиеся по сложному закону.
Случайная погрешность измерения – составляющая погрешность результата измерения одной и той же физической величины, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведённых с одинаковой тщательностью.
Эти погрешности (как систематические, так и случайные) могут вызываться различными причинами.
1. Инструментальная погрешность.
2. Погрешность метода измерений.
3. Погрешность измерения из-за изменения условий измерений.
4. Погрешность метода поверки – погрешность метода передачи размера единицы при поверке.
5. Погрешность градуировки СИ – погрешность действительного значения величины, приписанного той или иной отметке шкалы СИ в результате градуировки.
6. Погрешность воспроизведения единицы физической величины.
Промах – измерение, резко отличающееся от остальных результатов этого ряда. – грубая погрешность измерений.
Большую часть повышения производительности труда следует приписать внедрению во все отрасли промышленности современных машин и прогрессивных технологий. Инструмент с режущими кромками из карбида вольфрама, внедрение которого сдерживалось политикой международных картелей, которые не были заинтересованы в технических новшествах, чтобы не идти на экономические риски, связанные с затратами на капитальные вложения в новое производство.
С началом второй Мировой войны этот фактор перестал быть решающим. Станкостроительная промышленность сыграла большую роль в производстве больших масштабов прочных и надёжных станков, приспособленных для использвания инструмента с карбидной оснасткой.
Большая часть возросшей производительности труда была обеспечена благодаря широкому внедрению поточной технологии производства и множества её усовершенствований, в том числе такого новшества, как “контроль качества”.
Сущность принципа взаимозаменяемости деталей состоит в том, что размеры всякой детали выдерживаются в определённых пределах, называемых допусками. Из-за износа инструмента и по ряду других причин, станок, отлаженный на выпуск определённой продукции, утрачивает свою точность, пока погрешности не превысят допуски. Поэтому дальнейшую продукцию, изготавливаемую на таком станке, приходится браковать.
Прежде просто проверяли выборочные образцы и, когда обнаруживалось, что они не удовлетворяют принятым допускам, станок переналаживали. Но к этому времени на таком станке успевали изготовить много деталей с нарушением допусков, которые все подлежали отбраковке. Контроль качества, основанный на методах статистики, устраняет этот недостаток. Про разрешённым допускам вычисляют набор внутренних размеров. Когда число деталей, изготовленных с нарушением таких размеров, достигает определённого уровня, браковщик своевременно узнаёт, что точность станка скоро станет недостаточной. При этом с этого станка никаких деталей в брак ещё не попадает. Тогда станок останавливают без напрасных затрат времени и материалов.
Следует иметь в виду, что допуск назначается не от того, что мы не можем точно выполнить размер детали из-за несовершенства технологии. Как бы совершенна технология не была, всё равно идеальной точности добиться невозможно принципиально. Поэтому изготовление деталей – процесс двоякий.
1. Измерение изготовленной детали с некоторой заданной точностью, т.е. мы не знаем точного размера детали из-за несовершенства измерительного инструмента. Как бы точен он не был, всё равно точность его конечна, даже если и высока.
2.Изготовление с какой-то определённой точностью – т.е. мы не можем достичь идеального значения номинального размера. Следовательно, размеры изготовленной детали, если она годна, то есть попадают в поле допуска, могут занимать любое положение в пределах этого поля.
Какое же именно положение в пределах поля допуска они занимают, можно ли это узнать? Оказывается можно. Представим себе, что мы изготовили некоторое множество деталей с одним номинальным размером и с одним допуском.
N – общее число деталей, Td = dmax – dmin – разброс между максимальным и минимальным результатами измерений. Средний или номинальный размер, заданный чертежом – dном = x0.
Разобьём допуск Td на k небольших и равных между собой интервалов. Получится, что в интервалах близких к середине поля допуска окажется больше деталей, а в интервалах, близких к dmax либо к dmin – меньше. На основании этих данных можно построить ступенчатый график, который называется гистограммой. В каждом i -м интервале получилось ni деталей.

Здесь N называется выборкой по генеральной совокупности. Генеральная совокупность получается, если перейти к пределу при n → ∞ или D → 0, то есть


Чем больше число деталей в интервале, тем быстрее рост ступенчатой суммарной функции. Затем этот рост замедляется, так как при увеличении диаметра число деталей в интервале уменьшается. Как видно из графика, приращение высоты ступеньки замедляется.
- по этой формуле может быть вычислена средняя величина диаметра, а математическое ожидание при переходе к пределу:
При переходе к пределу ступенчатые графики превращаются в плавные кривые.

График плотности вероятности φ(x) означает вероятность попадания величины x в заданный бесконечно малый интервал Dx.
График функции распределения F(x) означает, что вероятность появления размера в пределах от dmin до dmax равна 1, а вероятность изготовления (или появления при переборе уже изготовленных деталей) размера x < dном равна 0.5.
Суммарный график может быть описан формулой:

Эта функция называется функцией нормального распределения или интегралом Лапласа. Здесь σ2 дисперсия по генеральной совокупности, а  среднее квадратическое отклонение случайной величины. Дисперсия по генеральной совокупности определяется по формуле:
среднее квадратическое отклонение случайной величины. Дисперсия по генеральной совокупности определяется по формуле:

Среднее квадратичное отклонение (СКО) – определено выше, в предыдущей лекции. При дифференцировании функции нормального распределения Лапласа F(x) получаем закон распределения вероятностей Гаусса:
Этими выражениями в таком виде пользоваться неудобно, поэтому их нормируют на величину:  . Тогда интеграл Лапласа F(z) и функция φ(z) – плотность вероятности нормированного нормального распределения будут соответственно иметь вид:
. Тогда интеграл Лапласа F(z) и функция φ(z) – плотность вероятности нормированного нормального распределения будут соответственно иметь вид:


Здесь F(z) – нормированная функция Лапласа, а φ(z) плотность вероятности нормированного распределения.
Расчёты показывают, что интеграл Лапласа приблизительно равен 1 в пределах ±3σ. Эта зависимость называется “правило 3σ”. Если подсчитать по этим формулам вероятность нахождения размеров в этом интервале, то получится, что эта вероятность в зависимости от заданных пределов следующая:
dном ± σ p ≈ 0.68
dном ± 2σ p ≈ 0.95
dном ± 3σ p ≈ 0.997
При измерениях необходимо так планировать количество опытов (измерений), чтобы оно не было слишком мало – для получения надёжного результата, но и не слишком велико, иначе увеличится время эксперимента. Заниженное число экспериментальных точек не позволит правильно оценить точность метода или средства измерения.
По результатам выборки и её объёму можно установить границы, внутри которых с определённой заданной вероятностью будут находиться значения дисперсии, СКО и dном – эти границы определяют доверительный интервал.
Соответствующую этому интервалу вероятность называют надёжностью или доверительной вероятностью. Это значит, что при определении доверительных границ интервала ± 3σ, вероятность нахождения измерения в этих границах равна p ≈ 0.997.
Интервал ± 3σ можно рассматривать как допуск, то есть Td = ± 3σ или как границы, в которые попадают погрешности измерений в зависимости от решаемой задачи: 1) изготовление детали, 2) измерение детали инструментом, погрешность которого известна.
Вообще говоря, определить вероятность нахождения размера можно в любом интервале, а не обязательно в указанных выше. Это делается так.
Например, нужно определить доверительные границы (доверительный интервал) значения некоторой измеряемой величины x с вероятностью P, если известно, что дисперсия этой величины равна σ.
Сначала по таблице интеграла вероятностей F(z) находят значение t, которое является отношением отклонения измеренного значения от его математического ожидания к среднему квадратическому отклонению
Так как доверительные границы располагаются симметрично по отношению к среднему значению x0 , то будет иметь место соотношение:
Отсюда находим доверительные границы x для среднего значения x0. Это значит, что истинное значение измеряемой величины с вероятностью P находится в границах:
Причём n = 1 так как измерения однократные. То есть считается, что так как распределение Гаусса и интеграл Лапласа получены для бесконечно большого числа испытаний (генеральной совокупности), то любое однократное измерение с вероятностью близкой к единице попадёт внутрь кривой (правило 3σ). Если задавать более узкий доверительный интервал, нужно провести вышеуказанный расчёт.
Рассмотрим случай, когда проводятся не однократные, а многократные измерения. Причём, число измерений ограничено выборкой. В этом случае необходимо проверить гипотезу соответствия выборки и генеральной совокупности. Другими словами проверить насколько распределение, полученное в результате нескольких измерений одной и той же величины, соответствует нормальному. Для проверки этой гипотезы существует формула критерия Стьюдента (Госсета).

В этой формуле ν = n – 1 – число степеней свободы, которое на единицу меньше количества проведённых испытаний (измерений), Γ — гамма-функция. Чем больше число степеней свободы, тем ближе распределение Стьюдента к нормальной функции, поэтому та и другая функции изображаются почти одинаковым графиком. Доверительные границы для многократных испытаний находят примерно также, как это делалось для однократных. Только в этом случае необходимо учитывать число проведённых опытов (степеней свободы).
Например, нужно найти доверительные границы истинного значения измеряемой величины, в которые попадают с заданной вероятностью P результаты n измерений некоторой величины
Сначала вычисляется по имеющейся выборке среднее значение измперяемой величины: и её среднее квадратическое отклонение:
Затем по таблице распределения Стьюдента в зависимости от числа степеней свободы и заданной вероятности находим коэффициент Стьюдента t, и находим доверительные границы в которых находится среднее значение измеренной величины близкое к истинному с заданной вероятностью:
Следовательно, при этом средний размер находится между значениями:
Если измеряются несколько независимых величин, то дисперсия их суммы равна сумме дисперсий этих величин:
σ2 (d1 + d2 + … + dn) = σ2(d1) + σ2(d2) +… + σ2(dn)
Среднее квадратическое отклонение (СКО) равно не сумме СКО нескольких независимых величин, а корню квадратному из суммы дисперсий, то есть:
Из этого следует важный вывод: погрешность нескольких независимых измерений равна не их сумме, а корню квадратному их этой суммы. То есть получается что-то вроде теоремы Пифагора, согласно которой гипотенуза всегда меньше суммы катетов (она равна сумме квадратов катетов, как известно), только не на плоскости, а распространённая на случай n измерений. По этой формуле мы будем считать погрешность блока концевых мер.
Интеграл Лапласа позволяет рассчитать доверительный интервал для однократного измерения. То есть результат получен один раз, но при этом считаем, что распределение измеряемой величины соответствует распределению Лапласа.
Средства контроля — информационные измерительные системы.
По функциональному назначению средства контроля разделяются на:
- измерительные системы
- системы автоматического контроля
- системы технической диагностики
- измерительно-вычислительные комплексы.
По организации алгоритма функционирования ИИС различаются на:
- ИИС с с заранее заданным алгоритмом функционирования, который не меняется, вследствие чего такая система применяется для исследования объектов, работающих в определённых режимах.
- Программируемые ИИС, алгоритм работы которых меняется в соответствии с заданной программой, связанной с условиями функыционирования исследуемого объекта.
- Адаптивные ИИС, в которых алгоритм работы изменяется, приспосабливаясь к изменениям измеряемых величин и условий работы объекта исследования; для этой системы требуется меньшее количество информации, что особенно важно при исследовании новых, малоизученных объектов.
Первые две ИИС, это системы пассивного контроля. Третья — система активного контроля с обратной связью, адаптирующаяся к изменяющимся внешним условиям. Она помогает вовремя диагностировать и исправить замеченных ошибки отклонения размеров за пределы поля допуска.
Простейшая схема обратной связи — станок — приспособление — инструмент — деталь.
Одним из методов активного контроля является метод акустической эмиссии — АЭ. По изменяющейся частоте звукового сигнала судят об изменении парамеров резания. Тогда включается система автоматическогоо регулирования и возвращает параметры резания к прежним значениям.
Измеряемая физическая величина непосредственно воздействует на первичный измерительный преобразователь, который является первым в цепи средства измерения. Конструктивно обособленные первичные преобразователи называются датчиками.
К измерительным преобразователям относят термопары, измерительные трансформаторы тока и напряжения, измерительные усилители, электромеханические измерительные механизмы, аналогоцифровые преобразователи и т.д.
Три закона роботехники.
- Робот не может причинить вред человеку или своим бездействием допустить, чтобы человеку был причинён вред.
- Робот должен повиноваться всем приказам, которые даёт человек, кроме тех случаев, когда эти приказы противоречат Первому Закону.
- Робот должен заботиться о своей безопасности в той мере, в которой это не противоречит Первому и Второму Законам.
Энтропия дискретного источника информации.
В теории информации есть понятие меры неопределённости, которое называется энтропией дискретного источника информации. Формально-математически это сумма произведений вероятностей на их логарифм взятая с обратным знаком. Если совсем просто, то это количество значений измеряемой величины и вероятность каждого из них.