Практическая работа № 6.
Тема: Определение сходимости рядов по признаку Даламбера. Определение сходимости знакопеременных рядов. Разложение функций в ряд Маклорена.
Цели: Научиться исследовать на сходимость числовые ряды и разлагать в степенной ряд элементарные функции.
Краткие теоретические сведения.
Определение 1. Числовым рядом называется выражение вида 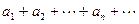 (1), где
(1), где 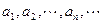 - числа, принадлежащие некоторой определенной числовой системе.
- числа, принадлежащие некоторой определенной числовой системе.
Для сокращенного обозначения рядов используется знак суммирования 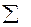 , а именно
, а именно 

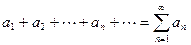 (2)
(2)
Примеры числовых рядов. Из членов бесконечной числовой последовательности можно составить ряд 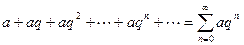 , который называется рядом геометрических прогрессий.
, который называется рядом геометрических прогрессий.
Ряд 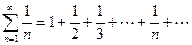 называется гармоническим рядом.
называется гармоническим рядом.
Определение 2. Сумма первых 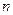 членов ряда называется частичной суммой ряда.
членов ряда называется частичной суммой ряда.
С рядом (2) связана последовательность его частичных сумм 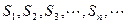 , где
, где 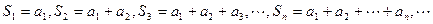 .
.
Определение 3. Ряд (1) называется сходящимся, если последовательность его частичных сумм сходится, т.е. существует конечный предел 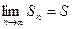 . Число
. Число 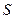 называется суммой ряда. Если
называется суммой ряда. Если 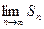 не существует или
не существует или 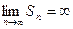 , то ряд называется расходящимся.
, то ряд называется расходящимся.
Гармонический ряд 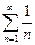 является расходящимся. Ряд геометрической прогрессии
является расходящимся. Ряд геометрической прогрессии 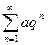 при
при 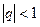 сходится, при
сходится, при 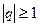 ряд геометрической прогрессии сходится лишь при
ряд геометрической прогрессии сходится лишь при 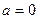 . Если
. Если 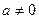 и
и 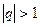 , то этот ряд расходится. Если
, то этот ряд расходится. Если 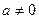 и
и 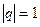 , то получаем при
, то получаем при 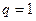 ряд
ряд 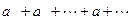 , а при
, а при 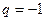 ряд
ряд 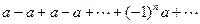 .
.
Свойства сходящихся рядов.
Теорема 1. Если ряд (2) сходится и его сумма равна 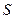 , то для произвольного числа
, то для произвольного числа 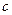 ряд
ряд 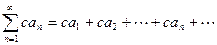 (3) также сходится и его сумма равна
(3) также сходится и его сумма равна 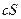 , если же ряд (2) расходится и
, если же ряд (2) расходится и 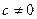 , то и ряд (3) расходится.
, то и ряд (3) расходится.
Теорема 2. Если ряды 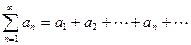 и
и 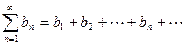 сходятся и их суммы равны соответственно
сходятся и их суммы равны соответственно 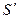 и
и 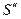 , то и каждый из двух рядов
, то и каждый из двух рядов
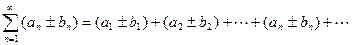 сходится и сумма каждого равна соответственно
сходится и сумма каждого равна соответственно 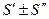 т.е. сходящиеся ряды можно почленно складывать и вычитать.
т.е. сходящиеся ряды можно почленно складывать и вычитать.
Следствие 1. Сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд.
Теорема 3. Если в ряде (1) добавить или отбросить конечное число членов, то полученный ряд 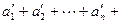 сходится или расходится одновременно с данным. В случае сходимости рассматриваемых рядов их суммы отличаются на сумму добавленных или отброшенных членов
сходится или расходится одновременно с данным. В случае сходимости рассматриваемых рядов их суммы отличаются на сумму добавленных или отброшенных членов
Определение 3. Ряд 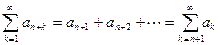 называется
называется 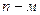 остатком ряда (1).
остатком ряда (1).
Следствие 2. Если ряд (1) сходится, то его остаток 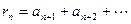 стремится к нулю при
стремится к нулю при 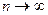 .
.
Теорема 4. Если ряд (2) сходится, то его общий член 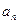 стремится к нулю.
стремится к нулю.
Если 
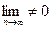 или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.
Признак Даламбера.
Теорема 5. Пусть дан ряд (1) с положительными членами. Допустим, что 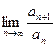 существует и
существует и 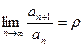 . Тогда:
. Тогда:
1) если 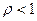 , то ряд (1) сходится;
, то ряд (1) сходится;
2) если 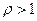 , то ряд (1) расходится.
, то ряд (1) расходится.
Замечание. При 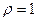 ряд
ряд 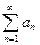 может как сходится, так и расходится. В этом случае необходимо дополнительное исследование.
может как сходится, так и расходится. В этом случае необходимо дополнительное исследование.
Пример 1. Исследовать сходимость ряда, используя признак Даламбера.
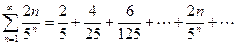 .
.
Подставляя в общий член ряда 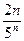 вместо
вместо 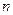 число
число 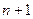 , получим
, получим 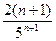 . Найдем предел отношения
. Найдем предел отношения 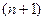 -го члена к
-го члена к 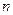 -му члену при
-му члену при 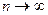 .
.
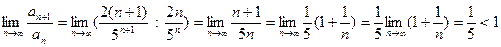 .
.
Следовательно данный ряд сходится.
Пример 2. Исследовать сходимость ряда, используя признак Даламбера.
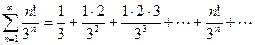 .
.
Имеем 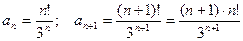 .
.
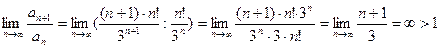 .
.
т.е. ряд расходится..
Пример 3. Исследовать сходимость ряда, используя признак Даламбера.
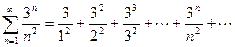 .
.
Имеем 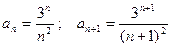 .
.
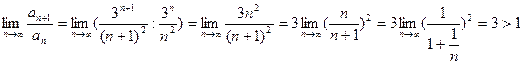 .
.
т.е. ряд расходится.
Знакопеременные ряды.
Определение 4. Ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными. 
Определение 5. Знакопеременный ряд 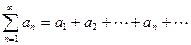 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 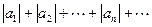 , составленный из модулей его членов.
, составленный из модулей его членов.
Определение 6. Ряд 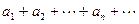 называется условно сходящимся, если он сходится, а ряд
называется условно сходящимся, если он сходится, а ряд 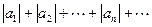 , составленный из модулей его членов, расходится.
, составленный из модулей его членов, расходится.
Определение 7. Ряд называется знакочередующимся, если положительные и отрицательные члены следуют друг за другом поочередно.
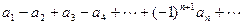 . (4)
. (4)
Теорема 6 (Лейбница). Знакочередующийся ряд (4) сходится, если:
1) его члены убывают по модулю,
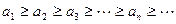 ,
,
2) его общий член стремится к нулю,

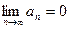 .
.
При этом сумма 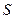 ряда (4) удовлетворяет неравенствам
ряда (4) удовлетворяет неравенствам 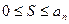 .
.
Пример 4. Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд
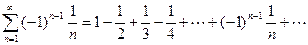 .
.
Члены данного ряда по модулю монотонно убывают: 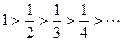 и
и 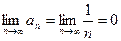 . Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно. Ряд
. Следовательно, согласно признаку Лейбница, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно. Ряд 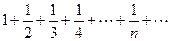 , составленный из модулей данного ряда является гармоническим рядом, который расходится. Поэтому данный ряд сходится условно.
, составленный из модулей данного ряда является гармоническим рядом, который расходится. Поэтому данный ряд сходится условно.
Пример 5. Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд 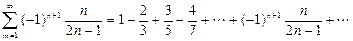 .
.
Члены данного ряда по модулю монотонно убывают: 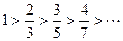 , но
, но
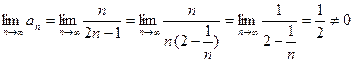 , Ряд расходится, так как признак Лейбница не выполняется.
, Ряд расходится, так как признак Лейбница не выполняется.
Пример 6. Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд.
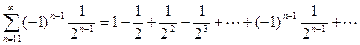 .
.
Используя признак Лейбница, получим 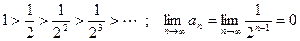 , т. е. ряд сходится. Рассмотрим ряд составленный из модулей членов данного ряда
, т. е. ряд сходится. Рассмотрим ряд составленный из модулей членов данного ряда
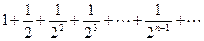 . Это геометрический ряд вида
. Это геометрический ряд вида 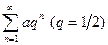 , который сходится Поэтому данный ряд сходится абсолютно.
, который сходится Поэтому данный ряд сходится абсолютно.
Пример 7. Исследовать сходимость знакопеременного ряда
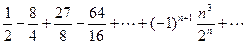 .
.
Исследуем, сходится ли заданный ряд абсолютно, для этого составим ряд из модулей членов данного ряда 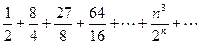 .
.  По признаку Даламбера имеем
По признаку Даламбера имеем
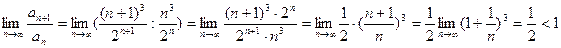 .
.
Так как предел отношения последующего члена к предыдущему меньше единицы, то ряд 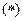 сходится. Отсюда вытекает, что данный ряд также сходится, и притом абсолютно. Определение 8. Ряд вида
сходится. Отсюда вытекает, что данный ряд также сходится, и притом абсолютно. Определение 8. Ряд вида 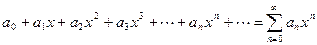 (5) называется степенным рядом.
(5) называется степенным рядом.
Числа 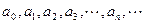 называются коэффициентами степенного ряда. Придавая
называются коэффициентами степенного ряда. Придавая 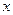 различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений
различные числовые значения, будем получать различные числовые ряды, которые могут оказаться сходящимися или расходящимися. Множество тех значений 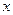 , при которых ряд (5) сходится называется областью его сходимости. Это множество никогда не пусто. так как любой степенной ряд сходится при
, при которых ряд (5) сходится называется областью его сходимости. Это множество никогда не пусто. так как любой степенной ряд сходится при 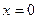 .
.
Теорема 7. Пусть существует конечный или бесконечный предел 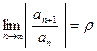 . Тогда:
. Тогда:
а) если  и
и 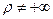 , то степенной ряд (5) сходится абсолютно в интервале
, то степенной ряд (5) сходится абсолютно в интервале 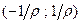 , т.е.при
, т.е.при 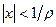 и расходится вне этого интервала, т.е. при
и расходится вне этого интервала, т.е. при 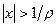 ;
;
б) если 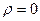 , то ряд (5) сходится при любом
, то ряд (5) сходится при любом 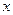 ;
;
в) если 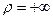 , то ряд (5) сходится лишь при
, то ряд (5) сходится лишь при 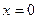 .
.
Определение 9. Число 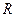 называется радиусом сходимости ряда (5), если при всех
называется радиусом сходимости ряда (5), если при всех 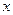 , для которых
, для которых 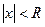 , ряд (5) сходится, а при всех
, ряд (5) сходится, а при всех 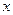 , для которых
, для которых 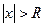 , ряд (5) расходится.
, ряд (5) расходится.
Радиус сходимости ряда (5) определяется по формуле 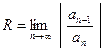 . (6)
. (6)
Определение 10. Интервал 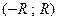 называется интервалом сходимости ряда (5).
называется интервалом сходимости ряда (5).
Если предел (6) равен нулю 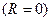 , то ряд (5) сходится в единственной точке
, то ряд (5) сходится в единственной точке 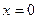 . На концах промежутка ряд может сходится (абсолютно или условно), но может и расходится. Сходимость ряда (5) при
. На концах промежутка ряд может сходится (абсолютно или условно), но может и расходится. Сходимость ряда (5) при 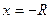 и
и 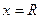 исследуется с помощью признаков сходимости.
исследуется с помощью признаков сходимости.
Пример 8. Найти промежуток сходимости степенного ряда
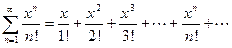 .
.
Используем формулу (6) получим 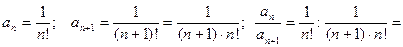
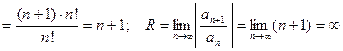 . Следовательно, промежуток есть
. Следовательно, промежуток есть 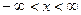 , т.е. данный ряд сходится на всей числовой прямой.
, т.е. данный ряд сходится на всей числовой прямой.
Пример 9. Найти промежуток сходимости степенного ряда
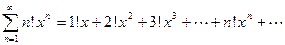 .
.
Согласно формулы (6), находим 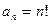 ;
; 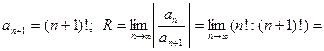
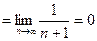 . Ряд сходится в одной точке
. Ряд сходится в одной точке 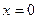 .
.
Пример 10. Найти промежуток сходимости степенного ряда
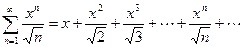 .
.
Используя формулу (6), получим
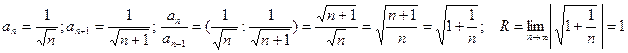 .
.
Следовательно данный ряд сходится абсолютно при 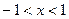 .
.
Исследуем сходимость ряда в точках 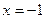 и
и 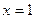 . При
. При 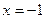 имеем
имеем
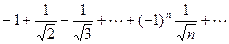 . Это знакочередующийся ряд, который в силу признака Лейбница сходится.
. Это знакочередующийся ряд, который в силу признака Лейбница сходится.
При 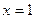 имеем
имеем 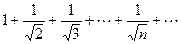 . Это гармонический ряд, который расходится, так как
. Это гармонический ряд, который расходится, так как 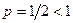 . Отсюда следует, что данный ряд сходится при
. Отсюда следует, что данный ряд сходится при 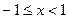 .
.
Пример 11. Найти промежуток сходимости степенного ряда
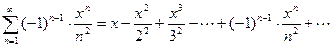 .
.
Согласно формуле (6) имеем 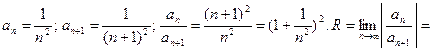
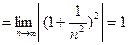 . Ряд сходится в промежутке
. Ряд сходится в промежутке 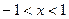 .
.
Исследуем сходимость ряда в точках 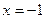 и
и 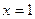 . При
. При 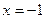 имеем знакочередующийся ряд
имеем знакочередующийся ряд 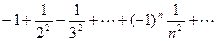 . В силу признака Лейбница он сходится. При
. В силу признака Лейбница он сходится. При 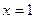 имеем ряд
имеем ряд 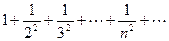 , есть гармонический ряд, который сходится, так как
, есть гармонический ряд, который сходится, так как 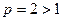 . Следовательно, данный ряд сходится в промежутке
. Следовательно, данный ряд сходится в промежутке 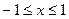 .
.
Определение 10. Ряд вида 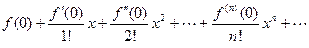 (7) называется рядом Маклорена.
(7) называется рядом Маклорена.
Пример 12. Составить ряд Маклорена для функции 
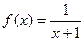 .
.
Вычислим значение функции и ее производных при 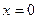 ; имеем
; имеем
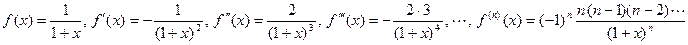 ;
;
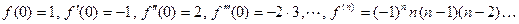 .
.
Подставив эти значения в формулу (7), получим разложение функции 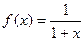 в ряд Маклорена
в ряд Маклорена
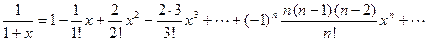 или
или
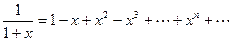 .
.
Задания для самостоятельной работы.
1.Исследовать сходимость ряда, используя признак Даламбера:
1.1 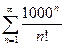 ; 1.2
; 1.2 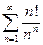 ; 1.3
; 1.3 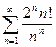 ; 1.4
; 1.4 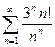 ; 1.5
; 1.5 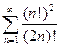 ; 1.6
; 1.6 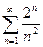 ; 1.7
; 1.7 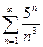 ;
;
1.8 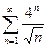 ; 1.9
; 1.9 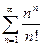 ;
;  1.10
1.10 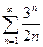 ; 1.11
; 1.11 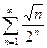 ; 1.12
; 1.12 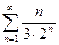 ; 1.13
; 1.13 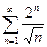 ; 1.14
; 1.14 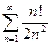 ; 1.15
; 1.15 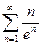 ; 1.16
; 1.16 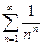 ; 1.17
; 1.17 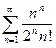 ; 1.18
; 1.18 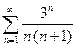 ; 1.19
; 1.19 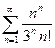 ; 1.20
; 1.20 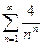 ;
;
1.21 
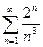 ; 1.22
; 1.22 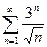 ; 1.23
; 1.23 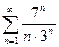 ; 1.24
; 1.24 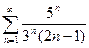 ; 1.25
; 1.25 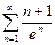 ; 1.26
; 1.26 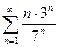 ;
;
1.27 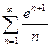 ; 1.28
; 1.28 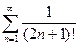 ; 1.29
; 1.29 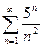 ; 1.30
; 1.30 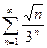 .
.
2. Исследовать сходимость (абсолютную или условную) знакочередующийся ряд.
2.1 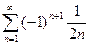 ; 2.2
; 2.2 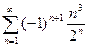 ; 2.3
; 2.3 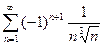 ; 2.4
; 2.4 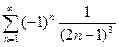 ; 2.5
; 2.5 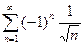 ;
;
2.6 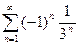 ; 2.7
; 2.7 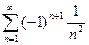 ; 2.8
; 2.8 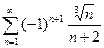 ; 2.9
; 2.9 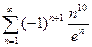 ; 2.10
; 2.10 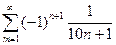 ;
;
2.11 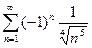 ; 2.12
; 2.12 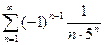 ; 2.13
; 2.13 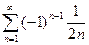 ; 2.14
; 2.14 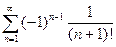 ;
;
2.15 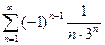 ; 2.16
; 2.16 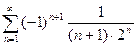 ; 2.17
; 2.17 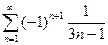 ; 2.18
; 2.18 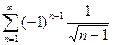 ;
;
2.19 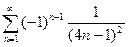 ; 2.20
; 2.20 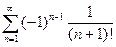 ; 2.21
; 2.21 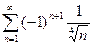 ; 2.22
; 2.22 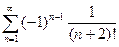 ;
;
2.23 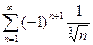 ; 2.24
; 2.24 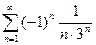 ; 2.25
; 2.25 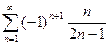 ; 2.26
; 2.26 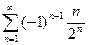 ;
;
2.27 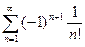 ; 2.28
; 2.28 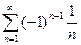 ; 2.29
; 2.29 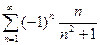 ; 2.30
; 2.30 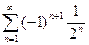 .
.
3. Найти радиус и промежуток сходимости степенного ряда.
3.1 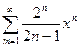 ; 3.9
; 3.9 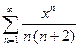 ; 3.17
; 3.17 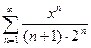 ; 3.25
; 3.25 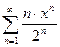 ;
;
3.2 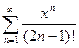 ; 3.10
; 3.10 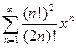 ; 3.18
; 3.18 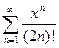 ; 3.26
; 3.26 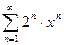 ;
;
3.3 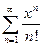 ; 3.11
; 3.11 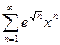 ; 3.19
; 3.19 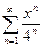 ; 3.27
; 3.27 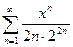 ;
;
3.4 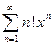 ; 3.12
; 3.12 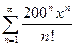 ; 3.20
; 3.20 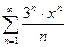 ; 3.28
; 3.28 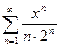 ;
;
3.5 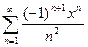 ; 3.13
; 3.13 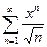 ; 3.21
; 3.21 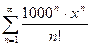 ; 3.29
; 3.29 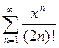 ;
;
3.6 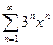 ; 3.14
; 3.14 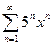 ; 3.22
; 3.22 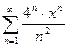 ; 3.30
; 3.30 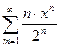 .
.
3.7 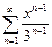 ; 3.15
; 3.15 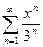 ; 3.23
; 3.23 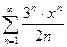 ;
;
3.8 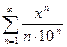 ; 3.16
; 3.16 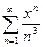 ; 3.24
; 3.24 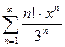 ;
; 
4. Разложить в ряд Маклорена функцию
4.1 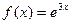 ; 4.4
; 4.4 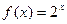 ; 4.7
; 4.7 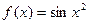 ; 4.10
; 4.10 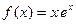 ; 4.2
; 4.2 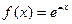 ; 4.5
; 4.5 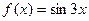 ; 4.8
; 4.8 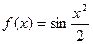 ; 4.11
; 4.11 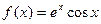 ;
;
4.3 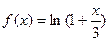 ; 4.6
; 4.6 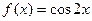 ; 4.9
; 4.9 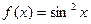 ; 4.12
; 4.12 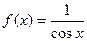 ;
;
4.13 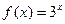 ; 4.18
; 4.18 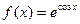 ; 4.24
; 4.24 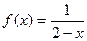 ; 4.29
; 4.29 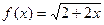 ;
;
4.14 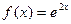 ; 4.19
; 4.19 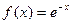 ; 4.25
; 4.25 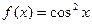 ; 4.30
; 4.30 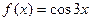 .
.
4.15 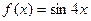 ; 4.20
; 4.20 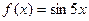 ; 4.26
; 4.26 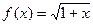 ;
;
4.16 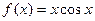 ; 4.21
; 4.21 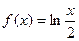 ; 4.27
; 4.27 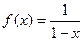 ;
;
4.17 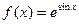 ; 4.22
; 4.22 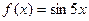 ; 4.28
; 4.28 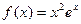 ;
;
Контрольные вопросы.
1. Что называется числовым рядом?
2. Какой ряд называется сходящимся?
3. Перечислить свойства сходящихся рядов.
4. Как формулируется необходимый признак сходимости числовых рядов?
5. Как формулируется признак Даламбера?
6. Какой ряд называется знакочередующимся рядом?
7. Как формулируется признак сходимости Лейбница?
8. Какой ряд называется абсолютно сходящимся?
9. Какой ряд называется условно сходящимся?
10. Какой ряд называется степенным?
11. Что называется радиусом сходимости степенного ряда?
12. Какова связь между радиусом сходимости степенного ряда и его интервалом сходимости?
13. Какой ряд называется рядом Маклорена для функции 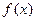 ?
?
14. Как разлагается функция 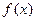 в ряд Маклорена?
в ряд Маклорена?