Практическая работа №5
Тема: Построение графиков степенных, показательных и логарифмических функций
Цель работы: Закрепить понятие области определения и множества значений функции, проверить практические умения при построении графиков функций.
Задание:
Изобразить схематически график функции, указать ее область определения и множество значений:
| 1. |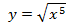 
| 4. |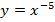 
|
| 2. |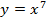 
| 5. |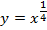 
|
| 3. |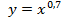 
| 6. |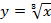 
|
Изобразить схематически график функции, указать ее область определения и множество значений:
| 7. |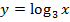 
| 10. |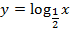 
|
| 8. |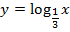 
| 11. |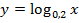 
|
| 9. |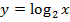 
| 12. | 
|
Изобразить схематически график функции, указать ее область определения и множество значений:
| 13. |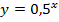 
| 16. |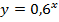 
|
| 14. |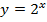 
| 17. |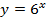 
|
| 15. |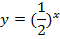 
| 18. |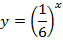 
|
Решить графически уравнение:
| 19. |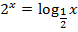 
| 22. |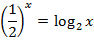 
|
| 20. |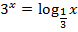 
| 23. |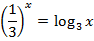 
|
| 21. |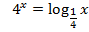 
| 24. |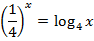 
|
Построить график функции:
| 25. |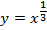 
| 28. |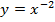 
|
| 26. |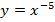
| 29. |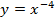 
|
| 27. |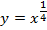
| 30. |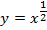 
|
Пояснение к работе:
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
основные свойства показательной функции y = a x при a > 1:
1. Область определения функции − вся числовая прямая
2. Область значений функции − промежуток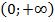 
3. Функция строго монотонно возрастает на всей числовой прямой, то есть, если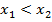 
, то 
4. График показательной функции с основанием a > 1 изображён на рисунке1.
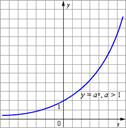1 рис.1
2 рис.2
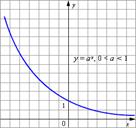
основные свойства показательной функции y = a x при 0 < a < 1:
1. Область определения функции − вся числовая прямая.
2. Область значений функции − промежуток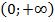
3. Функция строго монотонно убывает на всей числовой прямой, то есть, если 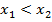,то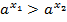 
4. График показательной функции с основанием 0 < a < 1 изображён на рисунке 2.
Степенная функция с целым показателем.
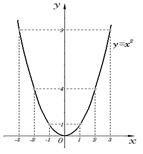
Квадратичная функция y=x2
основные свойства квадратичной функции:
1. D(f)= R;
2. E(f)=(0;+∞);
3. ограничена снизу на всей области своего существования;
4. принимает наименьшее значение в точке (0;0);
5. непериодическая;
6. четная;
7. возрастает на промежутке [0;+∞[ и убывает на промежутке ]-∞;0];
8. пересекает оси Oy и Ox в точке (0;0);
9. графиком является парабола, имеющая вершину в точке (0;0) и ветви которой направлены вверх;
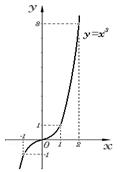
Кубическая функция y=x3
основные свойства кубической функции:
1. D(f)= R;
2. E(f)= R;
3. не ограничена ни снизу, ни сверху на всей области своего существования;
4. не принимает ни наибольших, ни наименьших значений;
5. непериодическая;
6. нечетная;
7. возрастает на R;
8. пересекает оси Oy и Ox в точке (0;0);
9. графиком является кубическая парабола, пересекающая начало координат;
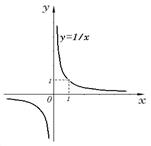
Обратная пропорциональность y=1/x.
основные свойства обратной пропорциональности y=1/x
1. D(f)= ]-∞;0[∪]0;+∞[;
2. E(f)= ]-∞;0[∪]0;+∞[;
3. не ограничена ни снизу, ни сверху на всей области своего существования;
4. не принимает ни наибольших, ни наименьших значений;
5. непериодическая;
6. нечетная;
7. убывает на всей области своего существования;
8. не имеет пересечений с осями координат;
9. имеет горизонтальную и вертикальную ассимптоты, которыми являются оси координат;
10. графиком является гипербола;
.
Логарифмическая функция.
основные свойства логарифмической функции y=logax
1. D(f)= ]0;+∞[;
2. E(f)= R;
3. неограниченая;
4. не принимает ни наибольшего ни наименьшего значения
5. непериодическая;
6. не является ни четной, ни нечетной;
7. возрастает при a>1, и убывает если 0<a<1;
8. пересекает ось абсцисс в точке (1;0);
9. графиком является график показательной функции y=ax зеркально отраженный от оси y=x
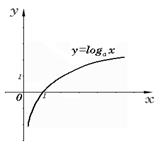
Рис.1 График логарифмической ф-и y=logax 1<a
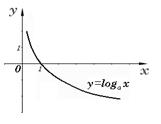
Рис.2 График логарифмической ф-и y=logax 0<a<1
Содержание отчета
1. Титульный лист в соответствии с СТП1.2-2005.
2. Цель работы
3. Задание
4. Выполненная практическая работа в соответствии с заданием
5. Ответы на контрольные вопросы
6. Вывод
Контрольные вопросы:
1) Дайте определение функции.
2) Дайте определение области определения функции.
3) Сформулируйте понятие графика функции.
4) Сформулируйте алгоритм нахождения точек пересечения графиков функций.
5) Сформулируйте алгоритм решения неравенств с помощью графиков функций.