Точечное оценивание параметров многомерной нормально распределенной генеральной совокупности.
Рассмотрим деятельность таможен Дальневосточного и Приволжского управления за август 2010 года. В качестве данных мы берем: количество работников в данной таможне, количество собак, имеющихся у кинологов на базе данной таможни, количество правонарушений выявленных на данной таможни в соответствии с КоАП РФ, количество выявленных преступлений на данной таможни в соответствии с УК РФ, количество человек получивших премию.
| Таможни Дальневосточного и Приволжского управления Y | Количество работников в данной таможне | Количество собак. имеющихся у кинологов на базе данной таможни | Количество правонарушений выявленных на данной таможни в соответствии с КоАП РФ | Количество выявленных преступлений на данной таможни в соответствии с УК РФ | Количество человек,получивших премию. |
| X1 | X2 | X3 | X4 | X5 | |
| Башкортастанская | |||||
| Нижегородская | |||||
| Оренбургская | |||||
| Пермская | |||||
| Самарская | |||||
| Саратовская | |||||
| Татарстанская | |||||
| Ульяновская | |||||
| Приволжская оперативная | |||||
| Амурская | |||||
| Благовещенская | |||||
| Биробиджанская | |||||
| Ванинская | |||||
| Владивостокская | |||||
| Дальневосточная оперативная | |||||
| Камчатская | |||||
| Магаданская | |||||
| Находнинская | |||||
| Сахалинская | |||||
| Уссурийская | |||||
| Хабаровская | |||||
| Хасанская | |||||
| Чукотская | |||||
| Якутская |
Для решения задачи взяли выборку объемом n=24, и она представлена в виде матрицы X – «объект-свойство», в которой содержатся все сведения обо всех объектах, вошедших в выборку.
Параметрами многомерного нормального закона распределения являются вектор математических ожиданий и ковариационная матрица.
Оценкой вектора m математических ожиданий является вектор средних арифметических.
X = 
Оценка ковариационной матрицы Σ обозначается ∧Σ и рассчитывается по формуле:

где Y – матрица центрированных значений исходных признаков.
Исправленная оценка ковариационной матрицы рассчитывается по формуле:

Будем искать оценку ковариационной матрицы и несмещенную оценку ковариационной матрицы с помощью программы GRETL.
Будем оценивать ковариационную матрицу для 3 признаков: x1,x2 и x3.
Исправленной оценкой ковариационной матрицы будет являться матрица S, имеющая вид:

А обратная ей матрица S1 выглядит так:

Затем строим доверительную область в форме параллелепипеда.
Как и вначале берем 3 признака – Х1, Х2, X3.
По формуле  , где k=3.
, где k=3.
То есть  =0,983.
=0,983.
Для построения используем статистику t, которая имеет распределение Стьюдента с (n-1) степенями свободы.

Находим s с помощью программы Gretl, для того чтобы строить доверительные интервалы. s=2,25437
Строим доверительный интервал для первого признака:



Так же строим доверительный интервал для второго признака:
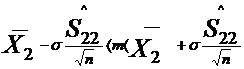
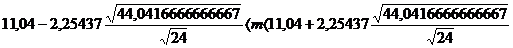
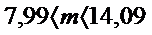
Теперь строим доверительный интервал для третьего признака:



Изображаем прямоугольник, чтобы в дальнейшем сравнить эту доверительную область с доверительной областью в форме эллипса.
Строим доверительную область в форме эллипса.
Выбираем 2 признака(k=2):X1 и X3.
Для построения данной доверительной области необходимо использовать собственные числа. Двойной клик на S выведет на исправленную оценку ковариационной матрицы, на S1 – обратную к ней. Жмем Свойства-Вид и видим собственные значения, которые нашли с помощью Gretl.
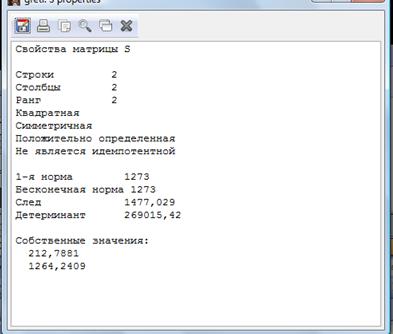
Чтобы оставить уравнение эллипса, сначала вычислим правую часть уравнения поверхности, где критическое значение для F будет равно:

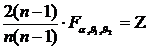 =
=  = 0,287
= 0,287
Составляем уравнение эллипса:
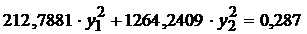
В правой части 2 – так как доверительную область строим для двух признаков, n – объем выборки, равный 24.
Приведем к каноническому виду:
Все необходимо поделить все на 0,287

Т.о.получаем:
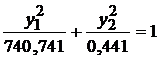
Числа в знаменателях – квадраты длин полуосей нашего искомого эллипса.
То есть:

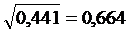
По полученным результатам, строим эллипс. При необходимости путем наложения эллипса на предыдущий прямоугольник, можно будет сравнить обе доверительные области.