Применение производной.
Одним из основных направлений применения производной является исследование поведения функций. Сформулируем необходимые для этого теоретические положения.
Первый признак существования экстремума: пусть функция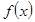 
непрерывна в некотором интервале содержащем критическую точку 
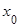, и дифференцируема во всех точках этого интервала. Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при 
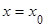функция имеет максимум. Если же при переходе через точку 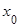слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
Второй признак существования экстремума: Если первая производная в точке 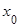равна нулю, а вторая производная отрицательна, то при 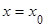функция имеет максимум. Если вторая производная положительна, то минимум.
Пример: исследовать на экстремумы функцию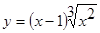 
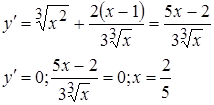
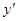+ max - min +
---------------.---------------.---------------------------
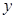
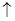0 
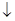2/5
Так как при х=0 производная не существует, эта точка также является критической. Точка х=0 является точкой максимума функции, а точка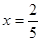 
точкой минимума функции.
Пример: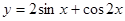 
Исследовать функцию на экстремумы.
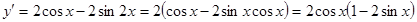
Исследуем эту функцию на экстремумы на отрезке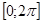 
, так как она периодическая с периодом 2π.
Решая уравнение,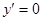 
или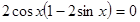 
, находим критические точки 
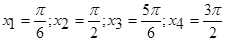Находим вторую производную:
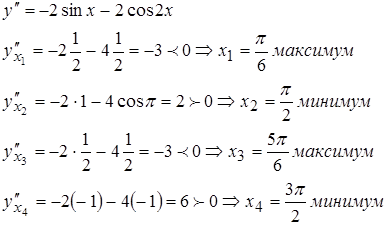
С помощью теории максимума и минимума решаются многие задачи геометрии, механики, биомеханики.
Понятие выпуклости – вогнутости кривой.
Определение. Функция называется вогнутой, если ее график лежит над касательной. Если график Функции лежит под касательной на некотором интервале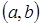 
, то функция называется выпуклой.
Переход графика функции от вогнутого к выпуклому или наоборот совершается в точках перегиба.
Теорема. Если во всех точках интервала 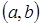вторая производная функции 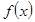отрицательна, то кривая выпукла, если вторая производная положительна, то вогнута
Наряду с этими понятиями для построения графика функции используется понятие асимптоты.
Определение. Прямая a называется асимптотой кривой, если расстояние от этой кривой до прямой при удалении в бесконечность стремится к нулю.
Различают вертикальные и наклонные асимптоты. Вертикальные асимптоты проходят через точки разрыва функции, то есть, точки в которых функция не определена.
Например, функция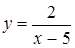 
имеет вертикальную асимптоту х=5.
Если кривая имеет наклонную асимптоту, заданную уравнением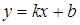 
, то коэффициенты k и b определяются по следующим формулам:
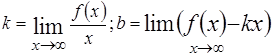
Пример. Найти промежутки выпуклости-вогнутости и асимптоты кривой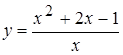 
.
+ -
------------ ------------
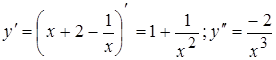
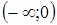функция вогнута;
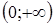функция выпукла.
x=0 – вертикальная асимптота.
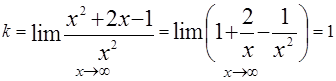
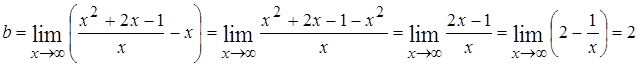
Таким образом,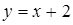 
наклонная асимптота.
Общая схема исследования функций:
1. Область определения функции.
2. Четность-нечетность, периодичность функции.
3. Корни функции.
4. Исследование на возрастание, убывание, экстремуму. Значение функции в экстремальных точках.
5. Исследование функции на выпуклость-вогнутость. Значение функции в точках перегиба.
6. Асимптоты функции.
7. Исследование функции при x, стремящемся к бесконечности.
8. Построение графика функции.