Найти частное решение, удовлетворяющее указанным начальным условиям.
131. 

 .
.
132. 

 .
.
133. 

 .
.
134. 

 .
.
135. 

 .
.
136. 

 .
.
137. 

 .
.
138. 

 .
.
139. 

 .
.
140. 

 .
.
В задачах 141–150 данную систему уравнений записать в матричной форме и затем решить с помощью обратной матрицы.
| 141. | 
| 142. | 
|
| 143. | 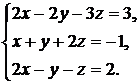
| 144. | 
|
| 145. | 
| 146. | 
|
| 147. | 
| 148. | 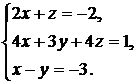
|
| 149. | 
| 150. | 
|
В задачах 151-160 исследовать сходимость числового ряда 
151.  . 152.
. 152. 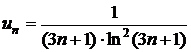 . 153.
. 153. 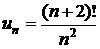 .
.
154.  . 155.
. 155. 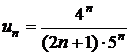 . 156.
. 156. 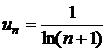 .
.
157.  . 158.
. 158.  . 159.
. 159.  .
.
160.  .
.
В задачах 161-170 найти интервал сходимости степенного ряда 
161. 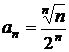 . 162.
. 162.  . 163.
. 163.  . 164.
. 164.  .
.
165.  166.
166.  . 167.
. 167.  .
.
168.  . 169.
. 169.  . 170.
. 170.  .
.
В задачах 171–180 заданы функция предложения некоторого товара S = S(p) и функция спроса q = q(p) относительно цены p.
Определить цену равновесия, т.е. цену, при которой спрос и предложение уравновешиваются, а также эластичность спроса и предложения для этой цены. Построить графики S = =S(p) и q = q(p). Как изменится цена при увеличении предложения на 0,2%? Как изменится цена при увеличении спроса на 0,3%?
171. 
 172.
172. 

173. 
 174.
174. 

175. 
 176.
176. 

177. 
 178.
178. 

179. 
 180.
180. 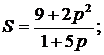

В задачах 181–190 найти вероятность событий
181. Завод изготовляет валики, каждый из которых имеет дефект с вероятностью p. Валик проверяется одним контролером, обнаруживающим дефект с вероятностью p1(если дефект не обнаружен, то валик идет в готовую продукцию). Кроме того, контролер может забраковать валик, не имеющий дефекта, с вероятностью α. Найти вероятности следующих событий:
А = «валик будет забракован»
В = «валик будет ошибочно забракован»
С = «валик, имеющий дефект, будет пропущен в готовую продукцию».
182. Истребитель атакует бомбардировщик, делает один выстрел и сбивает бомбардировщик с вероятностью p1. Если этим выстрелом бомбардировщик не сбит, то он стреляет по истребителю и сбивает его с вероятностью p2. Если истребитель этим выстрелом не сбит, то он еще раз стреляет по бомбардировщику и сбивает его с вероятностью p3. Найти вероятность следующих событий:
А = «сбит бомбардировщик»
В = «сбит истребитель»
С = «сбит хотя бы один самолет»
183. На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20%, второй – 46% и третьей – 34%. Известно, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй – 2%, а для третьей – 1%. Найдите вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось нестандартным.
184. В помещении завода имеется 5 одинаковых машин. Для каждой машины вероятность того, что она в данный момент работает, составляет 0,9. Найти вероятность того, что в данный момент работает по меньшей мере одна машина.
185. Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1 до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 6.
186. По данным одного из участков станции технического обслуживания автомобилей деталь А заменяется в среднем в 36% случаев, деталь В – в 42% случаев, а одновременно детали А и В подлежат замене в среднем в 30 % случаев аварий автомобилей.
а) Зависят ли одна от другой замена деталей А и В?
б) Найти вероятность того, что деталь В будет заменена, если деталь А уже заменена.
187. На трех станках при одинаковых и независимых условиях изготовляются детали одного наименования. На первом станке изготовляют 10%, на втором – 30%, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной равна 0.7, если она изготовлена на первом станке, 0.8 – если на втором станке и 0.9 – если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной. Оценить вероятность того, что бездефектная деталь была изготовлена на втором станке.
188. На студии телевидения установлены 3 камеры. Для каждой камеры вероятность того, что она включена в данный момент, составляет 0,6. Найти вероятность того, что в данный момент включена по меньшей мере одна камера.
189. В группу спортсменов входят 20 гребцов, 6 велосипедистов и 4 бегуна. Вероятность достижения требуемой квалификационной нормы составляет соответственно: 0.9, 0.8 и 0.75. Найти вероятность того, что выбранный в случайном порядке спортсмен достигнет требуемой нормы.
190. Вероятность, что расход электроэнергии в течение произвольно взятого часа не превысит установленной нормы, составляет p = 3/4. Найти вероятность того, что из ближайших 6 часов расход энергии в течение 4 часов не превысит нормы.