191. На двух автоматических станках производятся однотипные детали. Законы распределения числа X и Y выпускаемых в течение смены бракованных деталей соответственно для первого и второго станка заданы таблицами:
| X | Y | |||||||||
| P | 0,8 | 0,1 | 0,06 | ? | 
| 0,9 | 0,06 | 0,04 |
Составить закон распределения количества бракованных деталей, выпускаемых в течение смены на обоих станках, и вычислить математическое ожидание и среднее квадратическое отклонение этой случайной величины.
192. Вероятность того, что часы нуждаются в дополнительной регулировке, равна 0,2. Составить закон распределение количества часов, нуждающихся в дополнительной регулировке, среди трех случайно отобранных. По полученному закону распределения найти математическое ожидание и дисперсию этой случайной величины. Результат проверить по соответствующим формулам математического ожидания и дисперсии случайной величины, распределенной по биномиальному закону.
193. Из имеющихся шести билетов лотереи, из которых четыре невыигрышных, наудачу вынимают по одному билету до тех пор, пока не встретится выигрышный билет. Составить закон распределения случайной величины X – числа вынутых билетов, если каждый вынутый билет обратно не возвращается. Найти математическое ожидание и среднее квадратическое отклонение этой случайной величины.
194. Студент может сдавать экзамен не более четырех раз. Составить закон распределения случайной величины X – числа попыток сдать экзамен, если вероятность его сдачи – 0,75 и в дальнейшем возрастает на 0,1 при каждой следующей попытке. Найти дисперсию этой случайной величины.
195. Даны законы распределения двух независимых случайных величин X и Y:
| X | – 6 | Y | – 3 | – 1 | ||||
| P | 0,3 | 0,45 | 0,25 |
| 0,75 | 0,25 |
Составить закон распределения случайной величины X–Y и проверить свойство дисперсии D(X –Y) = D(X) + D(Y).
196. Среди пяти однотипных часов, имеющихся в мастерской, только в одних смещен маятник. Мастер проверяет наудачу взятые часы. Просмотр заканчивается, как только обнаружатся часы со смещенным маятником (проверенные часы снова не просматриваются). Составить закон распределения числа просмотренных мастером часов и вычислить математическое ожидание и дисперсию этой случайной величины.
197. Независимые случайные величины X и Y заданы законами распределения:
| X | Y | – 2 | ||||||
| P | 0,1 | 0,3 | ? |
| 0,4 | 0,6 |
Составить закон распределения случайной величины X2 + 2Y и проверить свойство математического ожидания: M(X2 + 2Y) = M(X2) + 2M(Y).
198. Известно, что случайная величина X, принимающая два значения x1 = 1 и x2 = 2, имеет математическое ожидание, равное 7/6. Найти вероятности, с которыми случайная величина X принимает свои значения. Составить закон распределения случайной величины 2 X2 и найти ее дисперсию.
199. Две независимые случайные величины X и Y заданы законами распределения:
| X | – 1 | Y | ||||||||
| P | 1/3 | 1/2 | 1/6 |
| 1/6 | 1/6 | 1/3 | 1/3 |
Составить закон распределения случайной величины Z = X2·Y. Найти функцию распределения этой случайной величины и построить ее график.
200. Две независимые случайные величины X и Y заданы законами распределения:
| X | – 1 | Y | – 1 | ||||||
| P | 1/4 | 1/2 | ? |
| 1/2 | 1/3 | ? |
Найти P(X= 3) и P(Y= 4). Составить закон распределения случайной величины X – 2Y и проверить свойства математического ожидания и дисперсии: M(X – 2Y) = M(X) – 2M(Y); D(X – 2Y) = D(X) + 4D(Y).
В задачах 201–210 заданы случайные величины, распределенные по нормальному закону
201. Случайная величина ξ распределена нормально. Найти Р(0< ξ<10), если Мξ= 10 и Р(10< ξ<20)= 0,3.
202. Случайная величина ξ распределена нормально. Найти Р(35< ξ<40), если Мξ= 25 и Р(10< ξ<15)= 0,2.
203. Случайная величина ξ распределена нормально. Найти Р(1< ξ<3), если Мξ= 3 и Р(3< ξ<5)= 0,1915.
204. Для случайной величины ξ, распределенной по нормальному закону, найти Р(|ξ–а|<σ).
205. Для случайной величины ξ, распределенной по нормальному закону, найти Р(|ξ–а|<2σ).
206. Для случайной величины ξ, распределенной по нормальному закону, найти Р(|ξ–а|<4σ).
207. Независимые случайные величины ξ и η распределены нормально,
Мξ= –1; Dξ= 2; Мη= 5; Dη= 7. Записать плотность вероятностей и функцию распределения их суммы. Найти Р(ξ+η<5) и Р(–1< ξ+η<3).
208. Независимые случайные величины ξ, η, ζ распределены по нормальному закону и Мξ= 3; Dξ= 4; Мη= –2; Dη= 0.04; Мζ= 1; Dζ= 0.09. Записать для их суммы плотность вероятностей и функцию распределения. Найти Р(ξ+η+ζ<5) и Р(–1< ξ+η+ζ<3).
209. Независимые случайные величины ξ, η, ζ распределены нормально и Мξ= –1; Dξ= 9; Мη= 2; Dη= 4; Мζ= –3; Dζ= 0.64. Записать для их суммы плотность вероятностей и функцию распределения. Найти Р(ξ+η+ζ<0) и
Р(–3< ξ+η+ζ<0).
210. Станок автомат изготовляет валики, контролируя их диаметры ξ. Считая, что ξ распределена нормально и а= 10 мм,σ= 0,1 мм, найти интервал, в котором с вероятностью 0.9973 будут заключены диаметры изготовленных валиков.
В задачах 211–220 выборка X объемом n =100 задана таблицей:
| xi | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ni | 20+(a+b) | 30–(a+b) |
где результаты измерений xi = 0,2·a +(i –1)·0,3·b; ni – частоты, с которыми встречаются значения xi.
1) построить полигон относительных частот wi =ni/n;
2) вычислить среднее выборочное 
, выборочную дисперсию DB и среднее квадратическое отклонение σB;
3) вычислить теоретические частоты 
. Построить график 
на одном рисунке с полигоном;
4) с помощью критерия χ2 проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости α = 0,05.
211. a = 4; b = 3; 212. a = 3; b = 2; 213. a = 5; b = 1; 214. a = 1; b = 4;
215. a = 3; b = 5; 216. a=2; b = 3; 217. a = 4; b = 1; 218. a = 2; b = 5; 219. a = 1; b = 2; 220. a = 5; b = 4.
В задачах 221–230 двумерная выборка результатов совместных измерений признаков X и Y объемом n = 100 задана корреляционной таблицей:
| X Y | y1 | y2 | y3 | y4 | y5 | nxi |
| x1 | – | – | – | |||
| x2 | – | – | ||||
| x3 | – | 8+a | 12+b | – | – | 20+(a+b) |
| x4 | – | – | 16–a | 14–b | – | 30–(a+b) |
| x5 | – | – | – | |||
| x6 | – | – | ||||
| x7 | – | – | – | |||
| nyi | 19+a | 42+b–a | 31–b | n = 100 |
где xi = 0,2·a +(i –1)·0,3·b; yi = 0,5·a +(j – 1)·0,2·b.
1) Найти 
и σy. Значения 
и σx взять из предыдущей задачи.
2) Вычислить коэффициент корреляции rB. Сделать вывод о характере связи между признаками X и Y.
3) Построить уравнение прямой линии регрессии Y на X в виде 
.
4) На графике изобразить корреляционное поле, т.е. нанести точки (xi, yi) и построить прямую 
.
221. a = 4; b = 3; 222. a = 3; b = 2; 223. a = 5; b = 1;
224. a = 1; b = 4; 225. a = 3; b = 5; 226. a = 2; b = 3;
227. a = 4; b = 1; 228. a = 2; b = 5; 229. a = 1; b = 2
230. a = 5; b = 4
В задачах 231–240 найти максимальное значение функции 
при условиях 
. Значения 
взять из таблицы
| Параметры | Варианты | |||||||||
| A1 | ||||||||||
| A2 | ||||||||||
| A3 | ||||||||||
| B1 | ||||||||||
| B2 | ||||||||||
| B3 | ||||||||||
| T1 | ||||||||||
| T2 | ||||||||||
| T3 | ||||||||||
| C1 | ||||||||||
| C2 |
требуется:
1) решить задачу линейного программирования графическим методом;
2) решить задачу табличным симплексным методом;
3) показать соответствие опорных решений и вершин области допустимых решений;
В задачах 241–250 некоторый однородный груз, сосредоточенный у трёх поставщиков Ai (
), необходимо доставить пяти потребителям Bj (
). Запасы груза у поставщиков ai и потребности потребителей bj, а также стоимости перевозки единицы груза от i-го поставщика j-му потребителю Cij заданы в таблице.
| Поставщики | Потребители | Запасы | ||||
| B1 | B2 | B3 | B4 | B5 | ||
| A1 | С11 | С12 | С13 | С14 | С15 | a1 |
| A2 | С21 | С22 | С23 | С24 | С25 | a2 |
| A3 | С31 | С32 | С33 | С34 | С35 | a3 |
| Потребности | b1 | b2 | b3 | b4 | b5 |
Требуется определить оптимальный план перевозок, позволяющий вывезти все грузы от поставщиков и удовлетворяющий потребности всех потребителей таким образом, чтобы этот план имел минимальную стоимость. Первый опорный план найти методом «северо-западного» угла. Оптимальный план найти методом потенциалов. Вычислить стоимость перевозок для каждого плана.
| Параметры | Варианты | |||||||||
| a1 | ||||||||||
| a2 | ||||||||||
| a3 | ||||||||||
| b1 | ||||||||||
| b2 | ||||||||||
| b3 | ||||||||||
| b4 | ||||||||||
| b5 | ||||||||||
| С11 | ||||||||||
| С12 | ||||||||||
| С13 | ||||||||||
| С14 | ||||||||||
| С15 | ||||||||||
| С21 | ||||||||||
| С22 | ||||||||||
| С23 | ||||||||||
| С24 | ||||||||||
| С25 | ||||||||||
| С31 | ||||||||||
| С32 | ||||||||||
| С33 | ||||||||||
| С34 | ||||||||||
| С35 |
В задачах 251-260 отрасли 
и 
осуществляют капитальные вложения в четыре объекта. С учетом особенностей вклада и местных условий прибыль отрасли в зависимости от объема финансирования выражается элементами платежной матрицы 
. Для упрощения задачи принять, что убыток отрасли равен прибыли отрасли . Найти оптимальные стратегии отраслей. Требуется:
1) свести исходные данные в таблицу и найти решение матричной игры в чистых стратегиях, если оно существует (в противном случае см. следующий п. 2);
2) упростить платежную матрицу;
3) составить пару взаимно двойственных задач, эквивалентную данной матричной игре;
4) найти оптимальное решение прямой задачи (для отрасли В) симплекс-методом;
5) используя соответствие переменных, выписать оптимальное решение двойственной задачи (для отрасли А);
6) дать геометрическую интерпретацию этого решения (для отрасли А);
7) используя соотношение между оптимальными решениями пары двойственных задач, оптимальными стратегиями и ценой игры, найти решение игры в смешанных стратегиях;
8) дать рекомендации по каждой отрасли.
вариант 1 вариант 2 вариант 3
вариант 4 вариант 5 вариант 6
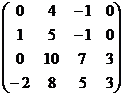
вариант 7 вариант 8 вариант 9
вариант10 
261 -270. Дано комплексное число Z. Требуется:
1) записать его в алгебраической и тригонометрической формах;
2) найти все корни уравнения ω3+z=0.
261. 
; 262. 
; 263. 
; 264. 
; 265. 
; 266. 
; 267. 
; 268. 
;
269. 
; 270. .
Содержание
1. Аналитическая геометрия и векторная алгебра ……………….. 4
2. Системы линейных уравнений и комплексные числа ………….. 5
3. Построение графиков функций, вычисление пределов
и выявление точек разрыва функций.…………….……………. 6
4. Производные функций, наибольшее и наименьшее значения
на отрезке..…………………………………………………….… 9
5. Исследование функций и построение графиков,
функции многих переменных, метод наименьших квадратов..… 11
6. Неопределенный, определенный и несобственный интеграл ….. 12
7. Решение дифференциальных уравнений и систем
дифференциальных уравнений …………….……….…….….…… 14
8. Кратные и криволинейные интегралы …………………………… 15
9. Исследование числовых и степенных рядов, приближенные
решения дифференциальных уравнений ………………...……… 17
10. Теория вероятностей ……………….……………………...……… 18
Петр Алексеевич Буров
Анатолий Николаевич Муравьев
Сборник заданий