Аксиома 2.
Не нарушая состояние АТТ к нему можно прикладывать или отбрасывать силы тогда и только тогда когда они составляют уравновешенную систему сил.
Следствие.
Не нарушая состояние тела точку приложения силы можно переносить вдоль линии ее действия. Из этого следствия вытекает что сила приложенная к АТТ представляет собой скользящий вектор.
Аксиома 3.
Не меняя состояние тела две силы приложенные к одной его точке можно заменить одной равнодействующей силой, приложенной в той же точке и равной их геометрической сумме(аксиома параллелограмма сил).
Аксиома 4.(Третий закон Ньютона)
Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны. Силы взаимодействия двух тел не составляют систему уравновешенных сил, так как приложены к разным телам.
Аксиома 5.
Равновесие деформируемого тела не нарушится, если жестко связать его точки и считать тело абсолютно твердым. Эту аксиому иногда называют принципом отвердевания.
3. Тело называется свободным, если его перемещения ничем не ограничены. Тело, перемещение которого ограничено другими телами называется не свободным, а тела ограничивающие перемещения данного тела называются связями. В точках контаката возникают силы взаимодействия между данным телом и связями. Силы с которыми связи действуют на данное тело, называются реакциями связей (реакциями). Направление реакции связи всегда противоположно тому направлению, по которому связь препятствует движению данного тела и определяется видом связи.
4. Сила, эквивалентная системе сил, называется равнодействующей данной системы сил:
Следует отметить, что не всякая система сил имеет равнодействующую.
5. Найдем равнодействующую двух действующих на твердое тело параллельных сил в двух случаях:
1. Силы направлены в одну сторону.
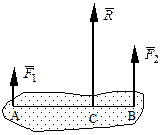
Равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону, равна по модулю сумме модулей слагаемых сил, им параллельна и направлена в туже сторону. Линия действия равнодействующей проходит между точками приложения слагаемых сил на расстояниях от этих точек, обратно пропорциональных этим силам.
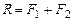 ,
,  . (1.15)
. (1.15)
2. Силы направлены в разные стороны.
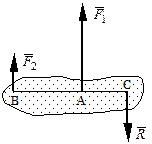 Равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в разные стороны, равна по модулю разности модулей слагаемых сил, им параллельна и направлена в сторону большей силы. Линия действия равнодействующей проходит вне отрезка, соединяющего точки приложения слагаемых сил, на расстояниях от этих точек, обратно пропорциональных силам.
Равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в разные стороны, равна по модулю разности модулей слагаемых сил, им параллельна и направлена в сторону большей силы. Линия действия равнодействующей проходит вне отрезка, соединяющего точки приложения слагаемых сил, на расстояниях от этих точек, обратно пропорциональных силам.
 ,
,  . (1.16)
. (1.16)
С помощью приведенных формул можно решать задачи и о разложении силы на две ей параллельные.
6. Моментом силы F относительно центра О называется
векторное произведение радиус-вектора точки приложения силы на силу:
Момент силы относительно центра есть вектор, перпендикулярный плоскости моментного треугольника и по модулю равный произведению модуля силы
на плечо, где плечо h-есть расстояние от центра до линии действия силы. Этот вектор направлен в ту сторону, откуда поворот, совершаемый телом под действием силы, виден происходящим против часовой стрелки.
Если точка О тела закреплена, то момент силы можно рассматривать как меру вращательного действия силы относительно этого центра. В декартовых координатах с началом в центре О можно записать:
Моментом силы относительно оси называется алгебраический момент проекции силы на плоскость перпендикулярную оси относительно точки пересечения оси с плоскостью
Если тело может вращаться вокруг данной оси, то момент силы можно рассматривать как меру вращательного действия силы относительно этой оси.
Знак момента силы относительно оси принято считать положительным, когда сила стремится повернуть тело против часовой стрелки, если смотреть с конца оси.
7. Парой сил называются две равные по модулю, параллельные и противоположные по направлению силы, приложенные к данному телу.
Расстояние между линиями сил пары называется плечом пары. Плоскость, проходящая через линии действия сил пары, называется плоскостью пары. Главный вектор пары сил равен нулю, следовательно, главный момент пары сил одинаков для любого полюса.
Эта величина называется момент пары и обозначается
Момент пары сил- вектор, перпендикулярный плоскости пары, направленный в ту сторону, откуда вращение тела парой видно против часовой стрелки, и по модулю равный произведению одной из сил пары на плечо.
Для плоской системы сил моменты пар отличаются лишь знаком и модулем, поэтому их можно рассматривать как величины алгебраические:
Свойства пар: 1.У пары можно произвольно менять силы и плечо, оставляя при этом неизменным момент пары. 2. Пару можно переносить в плоскости ее действия. 3. Пару можно переносить в плоскость, параллельную плоскости ее действия.
9. Теорема. Если твердое тело находится в равновесии под действием трех сил, и линии действия двух сил пересекаются, то линия действия третьей силы проходит через точку пересечения первых двух, и все три силы лежат в одной плоскости.
Доказательство:
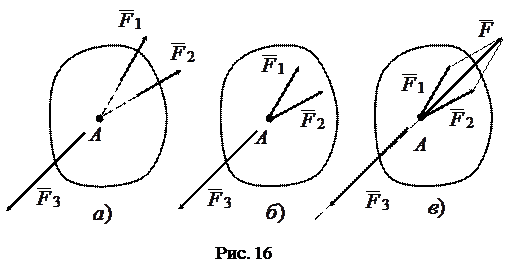
|
Пусть тело находится в равновесии под действием трех сил  ,
,  и
и  , причем линии действия
, причем линии действия  и
и  пересекаются в точке
пересекаются в точке 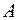 (рис. 16а).
(рис. 16а).
Согласно следствию 1 из аксиом статики, силы  и
и  можно, не нарушая состояние равновесия тела, перенести вдоль их линий действия в точку
можно, не нарушая состояние равновесия тела, перенести вдоль их линий действия в точку 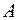 (рис. 16б), а затем по аксиоме 3 заменить одной силой
(рис. 16б), а затем по аксиоме 3 заменить одной силой  (рис. 16в), проходящей через точку пересечения сил
(рис. 16в), проходящей через точку пересечения сил  и
и  (точку
(точку 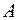 ) и лежащей с ними в одной плоскости, причем
) и лежащей с ними в одной плоскости, причем  . Тело находится в равновесии под действием двух сил
. Тело находится в равновесии под действием двух сил  и
и  (рис. 16в), следовательно, по аксиоме 1 они должны иметь общую линию действия, но тогда силы
(рис. 16в), следовательно, по аксиоме 1 они должны иметь общую линию действия, но тогда силы  ,
,  и
и  лежат в одной плоскости и их линии действия пересекаются в одной точке (точку
лежат в одной плоскости и их линии действия пересекаются в одной точке (точку 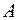 ).
).
10. Лемма. Силу можно переносить параллельно самой себе в любую наперед заданную точку, называемую центром приведения, присоединив к ней при этом пару, момент которой равен моменту первоначальной силы относительно центра приведения.
Доказательство.
 Пусть сила
Пусть сила  приложена в точке
приложена в точке 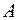 . Перенесем её в заданную точку
. Перенесем её в заданную точку  (рис. 40). Для этого в точке
(рис. 40). Для этого в точке  приложим силы
приложим силы 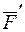 и
и  такие, что
такие, что 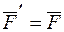 ,
,  . Тогда
. Тогда  . Момент пары равен:
. Момент пары равен:
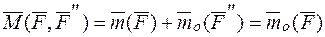 , так как
, так как  – линия действия силы
– линия действия силы  проходит через точку
проходит через точку  .
.
11. Приведение системы сил к простейшему виду
Возможность дальнейшего упрощения произвольных систем сил зависит от значения их главного вектора и главного момента, а также от удачного выбор центра приведения. При этом возможны следующие случаи:
a)  ,
,  . В данном случае система приводится к паре сил с моментом
. В данном случае система приводится к паре сил с моментом 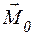 , значение которого не зависит от выбора центра приведения.
, значение которого не зависит от выбора центра приведения.
б)  ,
,  . Система приводится к равнодействующей, равной
. Система приводится к равнодействующей, равной  , линия действия которой проходит через центр О.
, линия действия которой проходит через центр О.
в)  ,
,  и взаимно перпендикулярны. Система приводится к равнодействующей, равной
и взаимно перпендикулярны. Система приводится к равнодействующей, равной  , но не проходящей через центр О (рис. 1.31).
, но не проходящей через центр О (рис. 1.31).

Рис. 1.31. Приведение системы сил к равнодействующей
Заменим главный момент 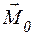 парой сил
парой сил 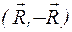 , как показано на рис. 1.31. Определим R из условия, что M0 = R h. Затем отбросим на основании второй аксиомы статики уравновешенную систему двух сил
, как показано на рис. 1.31. Определим R из условия, что M0 = R h. Затем отбросим на основании второй аксиомы статики уравновешенную систему двух сил 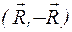 , приложенных в точке О.
, приложенных в точке О.
12. Произвольная система сил, приложенных к твердому телу, эквивалентна силе, равной главному вектору R, и паре сил с моментом, равным главному моменту L0 относительно какого-либо центра О. Чтобы такая система находилась в равновесии, необходимо и достаточно равенство нулю и главного вектора R, и главного момента L0. Поэтому условия равновесия пространственной системы сил могут быть представлены в векторной форме 
Два векторных условия эквивалентны следующим шести аналитическим условиям равновесия:

Условия равновесия можно сформулировать так: для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на оси декартовой системы координат равнялись нулю и суммы моментов всех сил относительно этих осей также равнялись нулю.
15. Центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.
Так как силу можно переносить вдоль линии ее действия в любую точку твердого тела, то принято считать, что сила тяжести тела приложена в его центре тяжести. При решении многих технических задач важно уметь определять положение центра тяжести, часто это можно сделать весьма простыми методами.
Иногда представляется возможность разбить тело на такие части, веса и положения центров тяжести которых известны. Задав положение Центров тяжести всех частей тела в декартовой системе координат, положение центра тяжести тела можно определить по формулам:
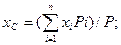
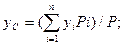

Методы нахождения центра тяжести
Наиболее часто для нахождения центра тяжести тела или фигуры применяют следующие методы:
- метод симметрии;
- метод разбиения;
- метод отрицательных масс.
Рассмотрим приемы, применяемые в каждом из перечисленных методов.
Метод симметрии
Представим себе однородное тело, которое имеет плоскость симметрии. Выберем такую систему координат, чтобы оси x и z лежали в плоскости симметрии (см. рисунок 1).

В этом случае каждой элементарной частице силой тяжести Gi с абсциссой yi = +a соответствует такая же элементарная частица с абсциссой yi = -a, тогда:
yC = Σ(Gixi)/ΣGi = 0.
Отсюда вывод: если однородное тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости.
Аналогично можно доказать и следующие положения:
- Если однородное тело имеет ось симметрии, то центр тяжести тела лежит на этой оси;
- Если однородное тело имеет две оси симметрии, то центр тяжести тела находится в точке их пересечения;
- Центр тяжести однородного тела вращения лежит на оси вращения.
Метод разбиения
Этот метод заключается в том, что тело разбивают на наименьшее число частей, силы тяжести и положение центров тяжести которых известны, после чего применяют приведенные ранее формулы для определения общего центра тяжести тела.