Простейшими называются тригонометрические уравнения следующих четырёх видов:
Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. К сожалению, на этом заключительном стандартном шаге школьники часто допускают ошибки, что ведет к потере баллов на ЕГЭ. Именно поэтому так важна данная тема.
Существуют два подхода к решению простейших тригонометрических уравнений.
Первый подход — бессмысленный и тяжёлый. Следуя ему, надо выучить по шпаргалке общие формулы, а также все частные случаи. Польза от этого столь же невелика, как от зубрежки шестнадцати строк заклинаний на непонятном языке. Мы отказываемся от такого подхода раз и навсегда.
Второй подход — логический и наглядный. Для решения простейших тригонометрических уравнений мы пользуемся тригонометрическим кругом и определениями тригонометрических функций.
Уравнения и
Напомним, что 
— абсцисса точки на единичной окружности, соответствующей углу 
, а 
— её ордината.
Из определения синуса и косинуса следует, что уравнения и имеют решения только при условии 
.
Абитуриент, будь внимателен! Уравнения 
или 
решений не имеют!
Начнём с самых простых уравнений.
. 
.
Мы видим, что на единичной окружности имеется лишь одна точка с абсциссой 1:
Эта точка соответствует бесконечному множеству углов: 
. Все они получаются из нулевого угла прибавлением целого числа полных углов 
(т. е. нескольких полных оборотов как в одну, так и в другую сторону).
Следовательно, все эти углы могут быть записаны одной формулой:
Это и есть множество решений данного уравнения. Напоминаем, что 
— это множество целых чисел.
. 
.
Снова видим, что на единичной окружности есть лишь одна точка с абсциссой 
:
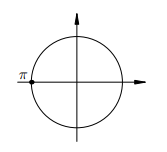
Эта точка соответствует углу 
и всем углам, отличающихся от на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:
. 
.
Отмечаем на тригонометрическом круге единственную точку с ординатой :
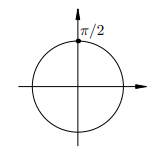
И записываем ответ:
. 
.
Обсуждать тут уже нечего, не так ли?:-)
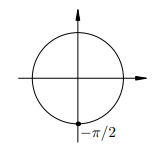
Можете, кстати, записать ответ и в другом виде:
Это — дело исключительно вашего вкуса.
Заодно сделаем первое полезное наблюдение. Чтобы описать множество углов, отвечающих одной-единственной точке тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить 
.
. 
.
На тригонометрическом круге имеются две точки с ординатой 0:
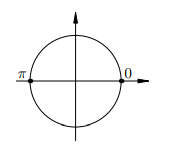
Эти точки соответствуют углам 
Все эти углы получаются из нулевого угла прибавлением целого числа углов (т. е. с помощью нескольких полуоборотов в обе стороны). Таким образом,
Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.
. 
.
Точки с абсциссой 0 также образуют диаметральную пару, на сей раз вертикальную:
Все углы, отвечающие этим точкам, получаются из — 
прибавлением целого числа углов (полуоборотов):
Теперь мы можем сделать и второе полезное наблюдение.
Чтобы описать множество углов, отвечающих диаметральной паре точек тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить 
.
Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или 
). Начинаем с косинуса.
. 
Имеем вертикальную пару точек с абсциссой 
:
Все углы, соответствующие верхней точке, описываются формулой (вспомните первое полезное наблюдение!):
Аналогично, все углы, соответствующие нижней точке, описываются формулой:
Обе серии решений можно описать одной формулой:
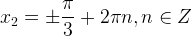
Остальные уравнения с косинусом решаются совершенно аналогично. Мы приводим лишь рисунок и ответ.
. 
. 
. 
. 
. 
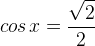
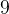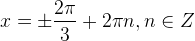
Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.
. 
Имеем горизонтальную пару точек с ординатой :
Углы, отвечающие правой точке:
Углы, отвечающие левой точке:
Описывать эти две серии одной формулой никто не заставляет. Можно записать ответ в таком виде:
Тем не менее, объединяющая формула существует, и её надо знать. Выглядит она так:
На первый взгляд совершенно не ясно, каким образом она дает обе серии решений. Но давайте посмотрим, что получается при чётных 
. Если 
, то
Мы получили первую серию решений 
. А если — нечетно, 
, то
Это вторая серия 
.
Обратим внимание, что в качестве множителя при 
обычно ставится правая точка, в данном случае 
.
Остальные уравнения с синусом решаются точно так же. Мы приводим рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.
. 
. 
. 
. 
. 
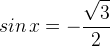
На этом с синусом и косинусом пока всё. Переходим к тангенсу.
Линия тангенсов.
Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная 
к единичной окружности, параллельная оси ординат (см. рисунок).
Из подобия треугольников 
и 
имеем:
Но 
, 
, 
, поэтому
Мы рассмотрели случай, когда находится в первой четверти. Аналогично рассматриваются случаи, когда находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.
Тангенс угла равен ординате точки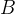 
, которая является точкой пересечения линии тангенсов и прямой 
, соединяющей точку с началом координат.
Вот рисунок в случае, когда находится во второй четверти. Тангенс угла отрицателен.
Уравнение
Заметим, что тангенс может принимать любые действительные значения. Иными словами, уравнение имеет решения при любом 
.
. 
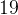Имеем диаметральную горизонтальную пару точек:
Эта пара, как мы уже знаем, описывается формулой:
. 
Имеем диаметральную пару:
Вспоминаем второе полезное наблюдение и пишем ответ:
Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.
. 
. 
. 
. 
. 
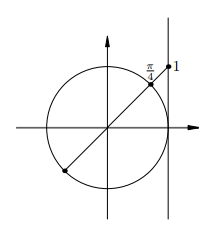
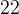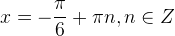
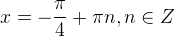
На этом заканчиваем пока и с тангенсом.
Уравнение нет смысла рассматривать особо. Дело в том, что:
уравнение 
равносильно уравнению ;
при 
уравнение равносильно уравнению 
.
Впрочем, существует также и линия котангенсов, но... Об этом мы вам расскажем на занятиях:-)
Итак, мы разобрали простейшие тригонометрические уравнения, содержащие в правой части табличные значения тригонометрических функций. Именно такие задачи встречаются в части В7 вариантов ЕГЭ.
Домашнее задание:
1.Составить конспект
2.Прочитать пар.№ 11.1
3.Решить из Учебника №11.2-11.4