Лабораторная работа № 3
Сравнение репрезентативности случайной, механической и серийной выборок из генеральной совокупности.
Цель работы: познакомиться с различными способами выборки объектов из генеральной совокупности. Оценить представительность выборок.
В данной работе студенты строят генеральные совокупности случайных распределений различных типов (равномерное, нормальное и так далее), а затем, используя различные стратегии выборки, оценивают представительность выборочных методов (качественно).
“Основной целью статистического анализа является выяснение некоторых свойств рассматриваемой генеральной совокупности. Если генеральная совокупность конечна, то наилучшая процедура — рассмотреть каждый ее элемент”[1].
Однако чаще всего на практике приходится ограничиваться выборочными значениями из генеральной совокупности. Основное требование к выборке — хорошо представлять (быть репрезентативной, представительной) генеральную совокупность.
Обычно считается, что чтобы иметь право судить о генеральной совокупности по выборке, выборка должна быть образована случайно. Это можно достичь различными способами (наиболее распространенными):
· собственно-случайная выборка;
· механическая;
· типическая;
· серийная.
Собственно-случайная выборка
Существует два подхода к решению данной задачи:
Простая случайная выборка с возвращением — объект извлекается из генеральной совокупности случайным образом, и, перед извлечением следующего, возвращается обратно (Например, после отбора деталей на анализ соответствия стандарту из большой партии, их снова возвращают назад и партию перемешивают);
Выборка без возвращения — извлеченный объект не возвращается в генеральную совокупность, а значит может появиться в выборке только один раз. (Например, отбор деталей производится с конвейера и после деструктивного анализа (разрушающего), возврат уже не возможен).
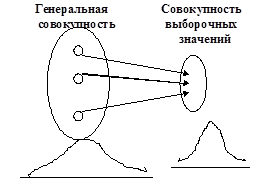
Рис. 19. Выборка элементов из генеральной совокупности
Если генеральная совокупность бесконечна, то процедуры выборки как с возвращением, так и без него, дают простую случайную выборку. Если генеральная совокупность конечна и велика по сравнению с размером выборки, то процедура извлечения без возвращения дает приблизительно простую случайную выборку. Если генеральная совокупность конечна и объем выборки составляет заметную долю от размера генеральной совокупности, то различие между этими двумя методами становитсязаметным.
Механическая выборка
Механической называется выборка, в которую объекты из генеральной совокупности отбираются через определенный интервал.
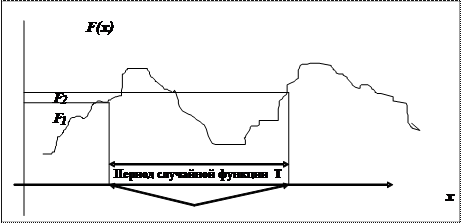
Рис. 20. Пример механической выборки из периодической случайной величины
Например, если объем выборки должен составлять 5% объема генеральной совокупности, то отбирается каждый двадцатый объект генеральной совокупности. Опасность, которая подстерегает исследователя при использовании этого метода — попасть в период периодически изменяющейся случайной величины (см. рис.20).
Типическая выборка
Если генеральную совокупность предварительно разбить на непересекающиеся группы, а затем образовать собственно-случайные выборки (с возвратом или без) из каждой группы и все отобранные объекты считать попавшими в выборку, то получим выборочную совокупность, называемую типической выборкой.
Считается, что типическая выборка с большей достоверностью воспроизводит однородную генеральную совокупность.
Серийная выборка
Если генеральную совокупность предварительно разбить на непересекающиеся серии (группы), а затем, рассматривая серии как элементы некой мегасовокупности, образовать из них собственно-случайную выборку (с возвратом или без) и все объекты отобранныхсерий считать попавшими в выборку, то получим выборочную совокупность, которая называется серийной.
Пример: На заводе 150 станков производят одинаковые изделия. Если отбирать изделия в выборку из тщательно перемешанной продукции всех 150 станков, то образуется собственно-случайная выборка. Но можно разделять продукцию станков и отбирать изделия отдельно из продукции первого, второго и так далее всех 150 станков. Это будет типическая выборка. Но если сначала случайным образом выбрать, например 15 станков и всю их продукцию считать попавшей в выборочную совокупность, то это будет серийная выборка.
ЗАДАНИЕ
Для выполнения работы сгенерируйте 1000 случайных чисел, распределенных нормально. Для этого воспользуйтесь специальным инструментом для генерации различных последовательностей чисел, подчиняющимся выбранным типам распределения (инструмент Анализ Данных в меню Сервис). Для набора данных в таблице со случайными числами с нормальным распределением некоторого признака, выполнить:
1. Считая распределение нормальным, принять набор данных за генеральную совокупность (всего данных — 1000).
2. Рассчитать параметры, которые характеризуют нормальное распределение (минимум, максимум, размах вариации, количество интервалов, частоту, среднее арифметическое, среднее квадратичное отклонение).
3. Построить полигон частот для заданной генеральной совокупности.
Анализ репрезентативности различных видов выборок.
Собственно-случайная выборка
4. Пронумеровать данные любым доступным способом.
5. Создать выборку – массив из 100 элементов, поместив в нее значения из генеральной совокупности, которые соответствуют номерам, сгенерированным случайным образом в диапазоне от 1 до 1000.
В качестве Генератора случайных чисел воспользоваться математическими функциями Excel — СЛЧИС() или СЛУЧМЕЖДУ(). Эти функции при каждом обращении генерируют одно, равномерно распределенное, число в заданном диапазоне.
6. Для полученной выборки рассчитать параметры нормального распределения и построить полигон частот.
Механическая выборка
7. Задать самостоятельно интервал выбора и выбрать для дальнейшей обработки из генеральной совокупности 100 значений.
8. Рассчитать параметры нормального распределения для данного типа выборки и построить полигон частот.
Серийная выборка
9. Разделить генеральную совокупность на 10 серий.
10. Выбрать самостоятельно одну серию данных и все ее значения считать серийной выборкой.
11. Рассчитать параметры нормального распределения для этой выборки.
12. Построить полигон частот для серийной выборки.
Выводы
На основании полученных данных сделать качественный вывод о репрезентативности различных методов получения выборочных данных. Сравнить параметры распределений и виды графиков (полигоны для этого случая построить на одном графике, выбрать режим XY-точечная диаграмма).
Справка по Excel
Для выбора чисел из генеральной совокупности (1000 — чисел) можно воспользоваться набором функций:
СЛЧИС() или СЛУЧМЕЖДУ() — генерация случайного числа. Первая функция возвращает значение в диапазоне [0,1]. Вторая — в диапазоне, заданном пользователем.
ФИКСИРОВАННЫЙ() — преобразование числа в текст в фиксированном формате.
СЦЕПИТЬ() — конкатенация (склейка) двух текстовых строк.
ДВССЫЛ() — ссылка на ячейку, указанную в аргументе, как на адрес, содержащий искомое значение. Например, если мы хотим получить значение, содержащееся в ячейке D4, то необходим вызов функции: =ДВССЫЛ(D4) (D4 — текст).
| A | B |  C C
| D | |
| а2 | ||||
 а51 а51
| ||||
| ¼ | ¼ | |||
| а1 | ||||
| а100 |
Рис. 3. Пример использования функций
Таким образом, получение заданной выборки сводится к созданию массива адресов (столбец В) и массива значений, выбранных по этим адресам (столбец С).
Функция ПРОСМОТР возвращает значение строки, столбца или из массива. Функция имеет две синтаксических формы: векторную и форму массива.
Диапазон. Две или более ячеек листа. Ячейки диапазона могут быть как смежными, так и несмежными.
Массив. Объект, используемый для получения нескольких значений в результате вычисления одной формулы или для работы с набором аргументов, расположенных в различных ячейках и сгруппированных по строкам или столбцам. Диапазон массива использует общую формулу; константа массива представляет собой группу констант, используемых в качестве аргументов.
| Предполагаемое действие | См. раздел | Использование |
| Просмотр диапазона, в который входят значения только одной строки или одного столбца (так называемый вектор), в поисках определенного значения и возврат значения из той же позиции второго диапазона. | Векторная форма | Векторная форма используется для просмотра значений в большом списке или значений, которые могут изменяться. |
| Просмотр первой строки или первого столбца массива, нахождение указанного значения и возврат значения из аналогичной позиции последней строки или столбца массива. | Форма массива | Форма массива используется для просмотра небольшого списка значений, которые остаются постоянными. |
Форма вектора
Вектор — это диапазон, содержащий только одну строку или один столбец. Векторная форма функции ПРОСМОТР просматривает диапазон, в который входят значения только одной строки или одного столбца (так называемый вектор), в поисках определенного значения и возвращает значение из соответствующей позиции второго диапазона. Эта форма функции ПРОСМОТР применяется, когда требуется указать диапазон, содержащий значения для сопоставления. Другая форма функции ПРОСМОТР автоматически выполняет поиск в первом столбце или первой строке.
ПРОСМОТР(искомое_значение; просматриваемый_вектор; [вектор_результатов])
Функция ПРОСМОТР в векторной форме имеет аргументы (Аргумент. Значение, предоставляющее информацию для действия, события, метода, свойства, функции или процедуры.), указанные ниже.
Искомое_значение - Обязательный аргумент. Значение, которое функция ПРОСМОТР ищет в первом векторе. Искомое_значение может быть числом, текстом, логическим значением, именем или ссылкой на значение.
Просматриваемый_вектор - Обязательный аргумент. Диапазон, состоящий из одной строки или одного столбца. Значения в аргументе просматриваемый_вектор могут быть текстом, числами или логическими значениями.
Важно. Значения в аргументе просматриваемый_вектор должны быть расположены в порядке возрастания:..., -2, -1, 0, 1, 2,..., A-Z, ЛОЖЬ, ИСТИНА; в противном случае функция ПРОСМОТР может возвратить неправильный результат. Текст в нижнем и верхнем регистрах считается эквивалентным.
Вектор_результатов - Необязательный аргумент. Диапазон, состоящий из одной строки или столбца. Вектор_результатов должен иметь тот же размер, что и просматриваемый_вектор.
[1] См. Лабораторную работу 1.