Основной закон динамики вращательного движения

Глава 3. Механика твердого тела

Момент инерции

Моментом инерции системы материальных точек относительно неподвижной оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до неподвижной оси вращения (рис. 3.2).

(3.1)

Для случая непрерывного распределения масс момент инерции определяется интегрированием

(3.2)

	Момент инерции представляет собой меру инертности твердого тела при вращательном движении (аналог массы при поступательном движении). Момент инерции зависит от
Рис. 3.1

формы, размеров тела и положения оси вращения.

В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (оси симметрии тела).

Разобьем цилиндр на отдельные концентрические цилиндры бесконечно малой толщины с внутренним радиусом r и внешним .

Момент инерции каждого такого цилиндра

(3.3)

где 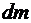– масса элементарного цилиндра, r – плотность тела; – элемент объема.

Массу элементарного цилиндра можно представить как

(3.4)

тогда

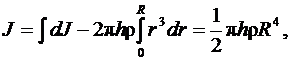(3.5)

так как масса цилиндра то

(3.6)

Если известен момент инерции тела относительно оси, проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера

(3.7)

Момент инерции относительно любой оси вращения равен моменту инерции J_о относительно параллельной оси, проходящей через центр масс плюс произведение массы тела на квадрат расстояния между осями (табл. 3.1).

Значения моментов инерции однородных тел

правильной геометрической формы

Кинетическая энергия вращающегося тела

	Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси ОО’. Мысленно разобьем тело на элементарные объемы с массами находящиеся на расстоянии от оси вращения.
Рис. 3.2

Линейные скорости элементарных объемов различны, а угловая одинакова, скорость их вращения т. е.

(3.8)

Кинетическая энергия вращающегося тела определится как сумма кинетических энергий элементарных объемов

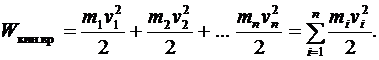(3.9)

так как

то

(3.10)

Если тело совершает одновременно вращательное и поступательное движение (например, цилиндр катится по горизонтальной поверхности), то кинетическая энергия Е_кин. складывается из энергии поступательного движения и энергии вращения, т. е.

(3.11)

где m – масса; J – момент инерции.

Основной закон динамики вращательного движения

Если тело, закрепленное на оси, приводится во вращение какой–либо касательной силой, то кинетическая энергия вращения возрастает за счет работы, производимой этой силой.

Под влиянием силы F тело за время dt повернется на угол d j, при этом точка приложения силы F переместится на ds.

Элементарная работа dA определяется как

(3.12)

где – расстояние от оси до точки приложения касательной силы; – момент силы относительно оси, проходящей через точку О.

	Момент силы равен произведению силы на ее плечо. Плечо силы – длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Рис. 3.3

Работа приложенной к телу силы приводит к увеличению кинетической энергии вращающегося тела,

Так как 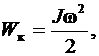то

j или 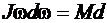j. (3.13)

Разделив левую и правую часть выражения (3.13) на dt, получим

(3.14)

Учитывая, что , а , окончательно получим

(3.15)

Момент силы относительно оси вращения равен произведению момента инерции относительно той же оси на угловое ускорение. Выражение (3.15) представляет собой основной закон динамики вращательного движения твердого тела относительно неподвижной оси. Если тело вращается под действием нескольких сил, то основной закон имеет вид

(3.16)