Cвойства определителей.
1.Определитель не меняется при транспонировании матрицы.
2.Если одна из строк (один из столбцов) определителя состоит из нулей, то определитель равен нулю.
3.Определитель, содержащий две одинаковые строки (столбца), равен нулю.
4.Определитель, содержащий две пропорциональные строки (столбца), равен нулю.
5.При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
6.Общий множитель элементов любой строки (столбца) можно вынести за знак определителя.
7.Величина определителя не изменится, если к одной из его строк (столбцов) прибавить другую строку (столбец), умноженную на какое угодно число.
Пример 7. Вычислить определитель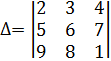 
.
Решение.
Вычислим этот определитель, разложив его по элементам третьего столбца. Для того чтобы упростить вычисления сделаем следующие преобразования: умножим третью строку на “-6” и прибавим её ко второй строке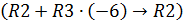 
; умножим третью строку на “-4” и прибавим ее к первой строке 
:
.
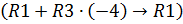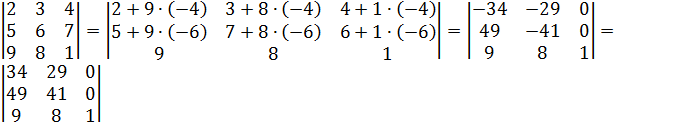Разложим определитель по элементам третьего столбца:
.
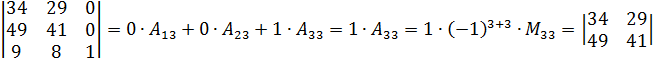Вычтем второй столбец из первого столбца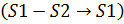 
:
.
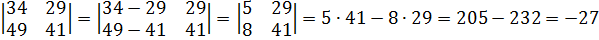Обратная матрица
Нахождение обратной матрицы с помощью присоединенной.
Обратная матрица может быть найдена по формуле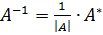 
, где 
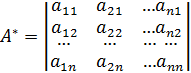матрица, составленная из алгебраических дополнений элементов матрицы 
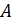и транспонированная. Матрица 
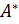называется присоединенной для матрицы .
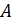Пример 1. Найти матрицу обратную матрице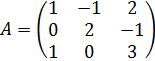 
.
Решение. Сначала проверяем, является ли матрица невырожденной: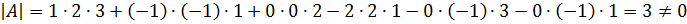 
⇒ матрица невырожденная и для нее существует обратная.
Найдем алгебраические дополнения для всех элементов матрицы :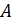
;
;
;
;
;
;
;
;
;
.
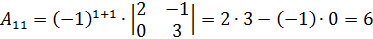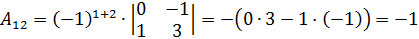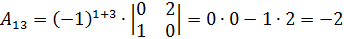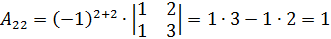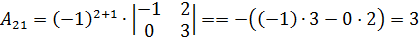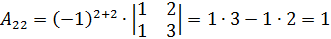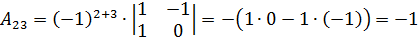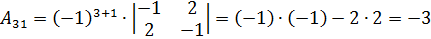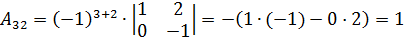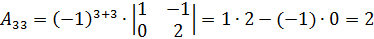Составим матрицу 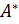, учитывая, что она транспонированная: 
.
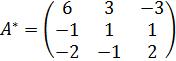Получим обратную матрицу:
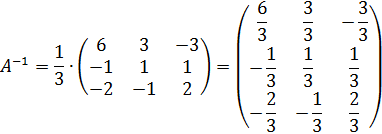
Проверка: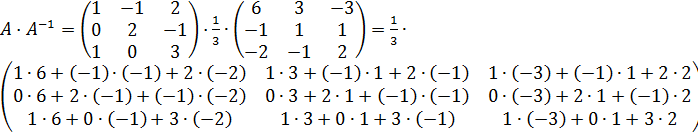 
= 
.
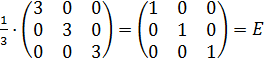Элементарными преобразованиями строк (столбцов) матрицы являются следующие:
1) отбрасывание нулевой строки (столбца);
2) умножение всех элементов строки (столбца) матрицы на число, отличное от нуля;
3) перестановка строк (столбцов) матрицы;
4) прибавление к одной строке (столбцу) другой строки (столбца), умноженной на любое число.
Две матрицы 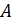и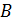 
называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается 
.
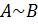Нахождение обратной матрицы с помощью элементарных преобразований.
Справа к данной невырожденной матрице 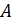приписать единичную матрицу 
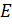того же порядка, что и матрица :
.
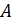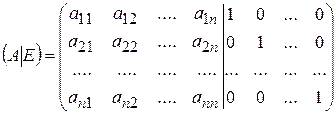Далее с помощью элементарных преобразований над строками объединенной матрицы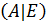 
привести матрицу 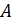к единичной матрице. Тогда на месте матрицы 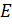окажется обратная матрица 
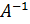, то есть будет получена матрица вида: 
.
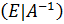Пример 2. 
Для матрицы 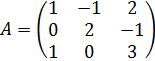из предыдущего примера найти обратную матрицу с помощью элементарных преобразований.
Решение. Так как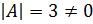 
⇒ обратная матрица существует.
Составим объединенную матрицу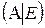 
: 
.
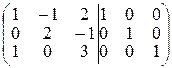Получим под главной диагональю нули: умножим все элементы первой строки на “-1” и прибавим их к соответствующим элементам третьей строки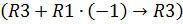 
:
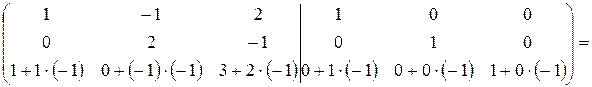
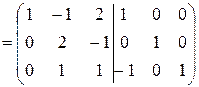
Поменяем местами вторую и третью строки: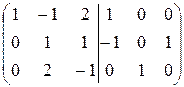 
.
Умножим вторую строку на “-2” и прибавим ее к третьей строке
:
.
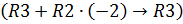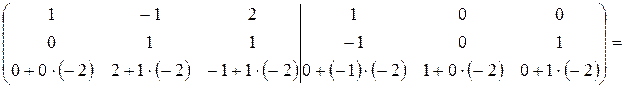
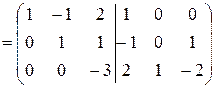Разделим третью строку на “-3”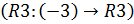 
: 
.
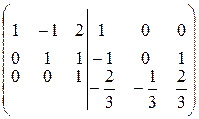Под главной диагональю получили нули на главной диагонали единицы.
Теперь получим нули над главной диагональю: умножим третью строку на “-1” и прибавим ее ко второй строке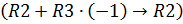 
; умножим третью строку на “-2” и прибавим ее к первой строке 
:
.
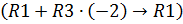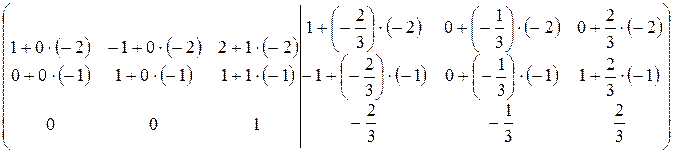
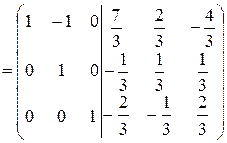Прибавим вторую строку к первой строке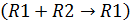 
:
= 
.
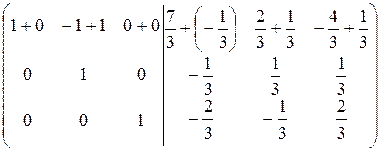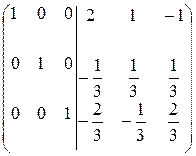Таким образом, получена матрица: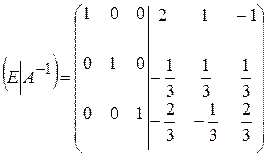 
.
Следовательно, обратная матрица:
.
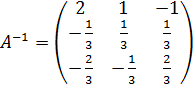Полученную матрицу можно сравнить с матрицей из предыдущего примера рассчитанную другим способом (они совпадают).