Начертательная геометрия
РАБОЧАЯ ТЕТРАДЬ
Факультет:
Группа:
Студент:
Нижний Новгород 2013
1. Комплексный чертеж точки
1. Построить трехкартинные комплексные чертежи точек:
А (5,10,15), B (15,0,20), C (0,20,15), D (20,15,0).






2. На чертеже без указания осей построить недостающую проекцию точки, если даны две ее проекции и постоянная прямая комплексного чертежа.

3. На чертеже без указания осей построить недостающую проекцию точки, если даны две ее проекции и три проекции точки А.

4. Построить недостающие проекции точек E, F, K, T, если известно, что точка E расположена перед точкой A, точка F – за ней; точка K расположена над точкой A, а точка T – под ней.




2. Прямая линия. Относительное положение точки и прямой
5. Концы отрезков AB, CD, EF, KL, MN, QR заданы координатами:
| A (30,15,10) | B (10,20,25); |
| C (30,20,10) | D (5,20,25); |
| E (30,15,5) | F (5,15,20); |
| K (20,10,25) | L (20,10,5); |
| M (25,10,25) | N (25,20,10; |
| Q (50,20,20) | R (10,30,30). |
· Построить три проекции каждого отрезка.
· Определить, как каждый отрезок расположен по отношению к плоскостям проекций.
· Указать, какие отрезки проецируются в натуральную величину на одну из плоскостей проекций.
· Определить углы наклона линий уровня к плоскостям проекций.






6. Дана прямая a общего положения. Построить проекции точек:
A – на прямой, B – над прямой, C – за прямой.

7. Зная, что точка C принадлежит отрезку AB, построить недостающую проекцию точки С.

| 8. Построить проекции отрезка MN длиной 35 мм, принадлежащего горизонтали. | 9. Через произвольную точку А провести горизонталь под углом 30° к П2. Сколько решений имеет задача? | |

| 
|
| 10. Построить недостающие проекции точек L и M, принадлежащих прямой l, проходящей через точку K. Построить проекции прямой l. | |

|
11. Через точку А провести горизонталь и фронталь, пересекающие прямую с общего положения.
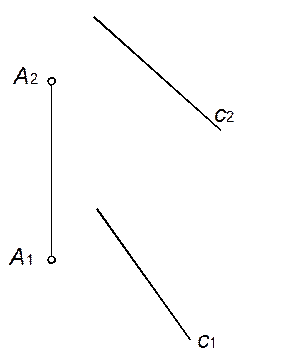

12. Прямые a и b пересечь горизонталью.

13. Скрещивающиеся прямые a и b пересечь фронтально-проецирующей прямой i, а прямые c и d пересечь горизонтально-проецирующей прямой g.


14. Через произвольную точку А провести прямую, параллельную заданной:
· прямой a общего положения;
· горизонтали h;
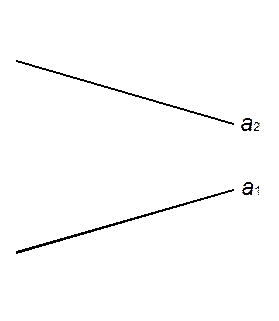

3. Плоскость и поверхность на комплексном чертеже
15. Плоскость задана точкой А и прямой а. Эту же плоскость задать: параллельными прямыми; пересекающимися прямыми; фронталью и горизонталью.



16. В плоскости a ( D ABC) провести горизонталь, а в плоскости
b (a // b) – фронталь.


17. Определить, принадлежат ли заданные точки A, B, C, D одной плоскости (рис. 31).

18. Достроить фронтальную проекцию плоского пятиугольника ABCDE.

19. Построить недостающую проекцию точки А, зная, что она принадлежит плоскости a (a × b); β (c // d).


20. Построить недостающую проекцию отрезка AB, принадлежащего плоскости a (f ´ h).

21. Построить недостающую проекцию треугольника ABC, лежащего в плоскости α (l × m).

22. Через точку M провести прямую, параллельную плоскости ψ (m × n).

23. Построить плоскость общего положения σ, проходящую через точку M и параллельную прямой m общего положения.
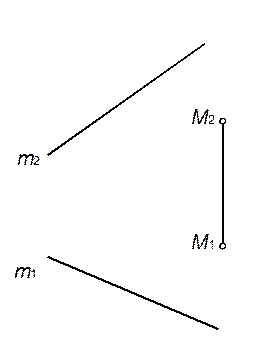
4. Точка на поверхности
| 24. Дана пирамида SABC. Построить горизонтальную проекцию точки E, лежащей в грани SBC. Через точку D, лежащую в грани SAB, провести в этой грани горизонталь. | 25. Дана призма LMN. Построить фронтальную проекцию точки F, лежащей в грани MN. Построить горизонтальную проекцию отрезка TR, лежащего в грани LN. | |

| 
|
| 26. Построить недостающие проекции точек: | |||
| A, B, C, D, лежащих на поверхности сферы, | E, F, K – на боковой поверхности цилиндра, | ||

| 
| ||
| L, M, N – на поверхности закрытого тора, | P,R,S, T, Q, V – на поверхности открытого тора. | ||

| 
| ||
2. сечение поверхности плоскостью
27. Построить проекции сечения многогранников проецирующей плоскостью δ.


28. Построить три проекции сечения пирамиды проецирующей плоскостью γ(γ1).

29. Построить проекции сечения сферы плоскостью δ (δ2).

30. Построить три проекции сферы с вырезом.

31. Построить три проекции цилиндра с вырезом.
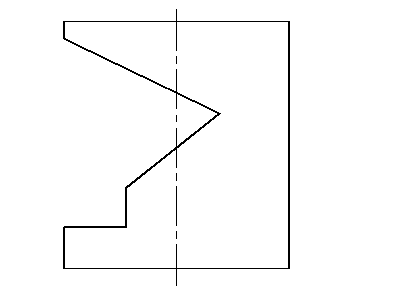
32. Построить проекции конуса с вырезом.

33. Дан конус вращения, поставленный основанием на плоскость П1. Построить фронтально-проецирующие плоскости, рассекающие конус по окружности, пересекающимся прямым, эллипсу, параболе и гиперболе. Построить проекции сечений.





34. Построить проекции сечения кольца плоскостью b(b1).


35. Построить недостающие проекции линии MN, принадлежащей поверхности конуса.
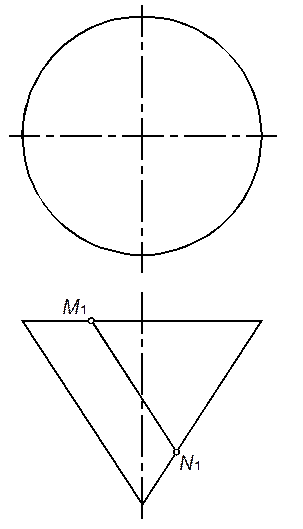

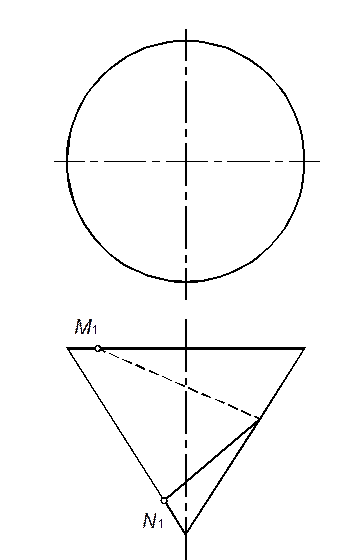
36. Построить недостающую проекцию линии MN, принадлежащей поверхности тора.

2. Позиционные задачи
| 37. Построить точку пересечения прямой а(a1,a2) и плоскости частного положения b(b2). | 38. Построить линию пересечения плоскости a (A, a) с плоскостью d (d2)^П2 | |

| 
|
39. Построить точку пересечения K прямой а с треугольником ABC и определить видимость прямой.


40. Построить точки пересечения прямой d с гранями многогранника и определить видимость прямой.

41. Построить точки пересечения поверхности сферы с прямой и определить видимость прямой.


42. Построить точки пересечения поверхности конуса с прямой и определить видимость прямой.

43. Построить точки пересечения поверхности с прямой a (a 1, a 2).

Вторая позиционная задача
44. Построить линию пересечения двух плоскостей a(c // d) и b(a × b).

45. Определить относительное положение двух плоскостей a (A, a) и b (c × d).

46. Построить линию пересечения двух треугольных непрозрачных пластин и определить их видимость.

47. Построить линию пересечения треугольной пластины и поверхности пирамиды и определить видимость, считая пластину и грани пирамиды непрозрачными.

48. Построить линию пересечения поверхностей, используя способ вспомогательных плоскостей уровня.



49. Построить линию пересечения поверхностей, используя метод концентрических сфер.
