Лекция ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ

 

Простой трубопровод постоянного сечения

Трубопровод называют простым, если он не имеет ответвлений. Простые трубопроводы могут быть соединены между собой так, что они образуют последовательное соединение, параллельное соединение или разветвленный трубопровод. Трубопроводы могут быть сложными, содержащими как последовательные, так и параллельные соединения или ветви разветвления.

Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад (разность) уровней энергии может быть создан тем или иным способом: работой насоса, благодаря разности уровней жидкости, давлением газа. В машиностроении приходится иметь дело главным образом с такими трубопроводами, движение жидкости в которых обусловлено работой насоса. В некоторых специальных устройствах при­меняется газобаллонная подача жидкости, т. е. используется давление газа. Течение жидкости за счет разности уровней (разности геометрических высот) осуществляется во вспомогательных устройствах, а также в гидротехнике и водоснабжении.

Рисунок 1. Схема простого трубопровода

 

Пусть простой трубопровод постоянного сечения расположен произвольно в пространстве (рисунок 1), имеет общую длину l и диаметр d и содержит ряд мест­ных сопротивлений. В начальном. сечении (1 — 1) геометрическая высота равна z₁ и избыточное давление Р₁, а в конечном (2 — 2) — соответственно z₂ и Р₂. Скорость потока и этих сечениях вследствие постоянства диаметра трубы одинакова и равна v.

Запишем уравнение Бернулли для сечений 1 — 1 и 2 — 2. Считая a₁=a₂ и исключая скоростные напоры, получаем

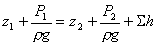
или

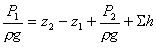
Пьезометрическую высоту, стоящую в левой части уравнения назовем потребным напором Н_{потр .} Если же эта высота задана, то будем называть ее располагаемым напором Н_расп. Как видно из формулы, этот напор складывается из геометрической высоты Dz=z₂-z₁, на которую поднимается жидкость в процессе движения по трубопроводу, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.

Сумма двух первых слагаемых Dz+ P₂/(rg) есть статический напор, и его можно представить как некоторую эквивалентную гео­метрическую высоту Н_ст подъема жидкости, а последнее слагаемое Sh — как степенную функцию расхода, тогда

Н_потр= Н_ст+Sh= Н_ст+KQ^m, (1)

где величина К, называемая сопротивлением трубопровода, и показатель m имеют разные значения в зависимости от режима течения.

Для ламинарного течения при замене местных сопротивлений эквивалентными длинами получим

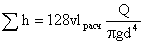
Следовательно,

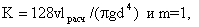(2)

где l_расч=l+l_экв.

Для турбулентного течения, выражая скорость через расход, получаем:

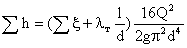
следовательно,.

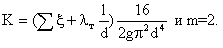(3)

 

 

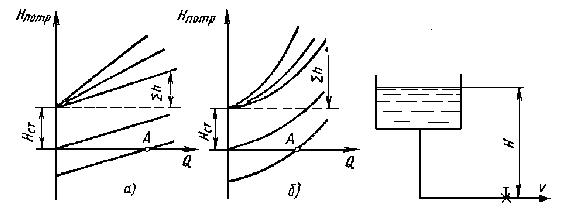
Рисунок 2. Зависимости потребных напоров от расхода жидкости в трубопроводе

Рисунок 3. Схема самотечного трубопровода

 

Формула (1), дополненная выражениями (2) и (3), является основной для расчета простых трубопроводов. По ней можно построить кривую потребного напора, т. е. его зависимость от рас­хода жидкости в трубопроводе. Чем больше расход, который необ­ходимо подавать по трубопроводу, тем больше потребный напор. При ламинарном течении эта кривая изображается прямой линией (или близкой к прямой при учете зависимости l_экв от Re), при турбулентном — параболой с показателем степени, равным двум (при l_т = const) или близким к двум (при учете зависимости l_т от Re). Величина Н_ст положительна в том случае, когда жидкость подни­мается или движется в полость с повышенным давлением, и отрица­тельна при опускании жидкости или движении в полость с разреже­нием.

Крутизна кривых потребного напора для ламинарного (рисунок 2, а) и турбулентного (рисунок 2, 6) режимов течения зависит от сопротивления трубопровода К и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений. Кроме того, при ламинарном течении наклон кривой (которую для этого течения можно считать прямой) изменяется пропорционально вязкости жидкости.

Точка пересечения кривой потребного напора с осью абсцисс при Н_ст=Dz=0 (точка А) определяет расход при движении жид­кости самотеком, т. ё. за счет лишь разности геометрических высот Dz. Потребный напор в этом случае равен нулю, так как давление в на­чале и в конце трубопровода равно атмосферному (за начало трубопровода считаем свободную поверхность в верхнем резервуаре); такой трубопровод условимся называть самотечным (рисунок 3). Если в конце самотечного трубопровода происходит истечение жид­кости в атмосферу, то в уравнении (1) для потребного напора к потерям напора следует добавить скоростной напор. Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода.

Характеристикой трубопровода называется зависимость суммар­ной потери напора (или давления) в трубопроводе от расхода: Sh=f(Q).

Таким образом, характеристика трубопровода представляет собой кривую потребного напора, смещенную в начало координат. Харак­теристика трубопровода совпадает с кривой потребного напора при Н_ст = 0, например, когда трубопровод лежит в горизонтальной плоскости, а противодавление Р₂ отсутствует.

Рассмотрим возможные задачи на расчет простого трубопровода.

Задача 1. Исходные данные: расход Q, давление Р₂, свойства жидкости (r и n), размеры трубопровода, а также материал и качество поверхности трубы (шероховатость). Найти потребный напор Н_потр.

Решение. По расходу и диаметру d трубопровода находит скорость тече­ния по v, d и n определяют Rе и режим течения. Затем по соответствующим формулам (или опытным данным) оценивают местные сопротивления (l_экв/d или при ламинарном и при турбулентном течении); по Re и шероховатости определяют коэффициент l и, наконец, решают основное уравнение (1) относительно H_потр.

При ламинарном течении рассчитывать l не обязательно, можно сразу определить К по формуле (2).

Задача 2. Исходные данные: располагаемый напор Н_расп, свойства жидкости, все размеры и шероховатость трубопровода. Найти расход Q.

Решение. Задаются режимом течения, основываясь па вязкости жидкости, так как решение существенно различно для ламинарного и турбулентного течения.

Режим течения в данном случае можно определить сравнением Н_расп с критическим его значением Н_кр, которое может быть выражено на основе формул (1) и (2) следующим образом:

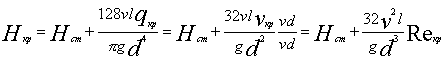
1. При ламинарном течении и замене местных сопротивлений эквивалент­ными длинами задача решается просто: из уравнения (1) с учетом формулы (2) находят расход Q; при этом вместо Н_потр подставляют Н_расп.

2. При турбулентном течении задачу надо решать методом последовательных приближений или графически.

В первом случае имеют одно уравнение (1) с двумя неизвестными Q и l_т. Для решения задачи задают значение коэффициента l_т с учетом шерохо­ватости. Так как этот коэффициент изменяется в сравнительно узких преде­лах (l_т = 0,015 - 0,04), большой ошибки при этом не будет, тем более, что при дальнейшем определении Q коэффициент l_т оказывается под корнем.

Решая уравнение (1) с учетом выражения (3) относительно Q, находят расход в первом приближении. По найденному Q определяют Re в пер­вом приближении, а по Re — уже более точное значение l_т. Снова подставляют полученное значение в то же основное уравнение и решают его относительно Q. Найдя расход во втором приближении, получают большее или меньшее раcхождение с первым приближением. Если расхождение велико, то расчет продолжают в том же порядке. Разница между каждым последующим значением Q и предыдущим будет делаться все меньше и меньше.

Обычно бывает вполне достаточно двух или трех приближений для полу­чения приемлемой точности.

Для решения той же задачи графическим способом строят кривую потреб­ного напора для данного трубопровода с учетом переменности l_т, т. е. для ряда значении Q подсчитывают v, Re, l_т и, наконец, Н_потр по формуле (1). Затем, построив кривую Н_потр от Q и зная ординату Н_потр = Н_расп, находят соответ­ствующую ей абсциссу, т. е. Q.

Задача 3. Исходные данные: расход Q, располагаемый напор Н_расп, свой­ства жидкости и все размеры трубопровода, кроме диаметра. Найти диаметр трубопровода.

Решение. Основываясь на свойствах жидкости (n), задают режим течения. Режим течения можно определить сравнением Н_расп с Н_кр, который равен (при данном Q)

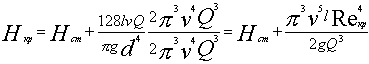
Для ламинарного течения задача решается просто на основе уравнения (1) с учетом выражения (2), а именно:

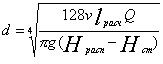
Определив d, выбирают ближайший большой стандартный диаметр и по тому же уравнению уточняют значение напора при заданном Q или наоборот.

При турбулентном течении решение уравнения (1) с учетом выраже­ния (3) относительно d лучше всего выполнить следующим образом: задать ряд стандартных значений d и для заданного Q подсчитать ряд значений Н_потр, затем построить график зависимости Н_потр от d и по заданному Н_расп по кривой определить d, выбрать ближайший большой стандартный диаметр и уточнить Н_потр.

 

Соединения простых трубопроводов

Последовательное соединение. Возьмем несколько труб, напри­мер, 1, 2 и 3 различной длины, разного диаметра и содержащих раз­личные местные сопротивления, и соединим их последовательно (рисунок 4, а). В результате получим простой трубопровод переменного сечения.

Очевидно, что при подаче жидкости по такому трубопроводу расход во всех последовательно соединенных трубах один и тот же, а полная потеря напора между точками М и N равна сумме потерь напора во всех последовательно соединенных трубах, т. е. имеем следующие основные уравнения:

Q₁ = Q₂ = Q₃ = Q;

Sh_M-N = Sh₁ + Sh₂ + Sh₃. (4)

Эти уравнения определяют правило построения характеристик последовательного соединения труб. Пусть даны характеристики трубопроводов 1, 2 и 3 (рисунок 4, б). Чтобы построить характери­стику всего последовательного соединения М — N, следует в соот­ветствии с выражением (4) сложить потери напора при одинако­вых расходах, т. е. сложить ординаты всех трех кривых при равных абсциссах.

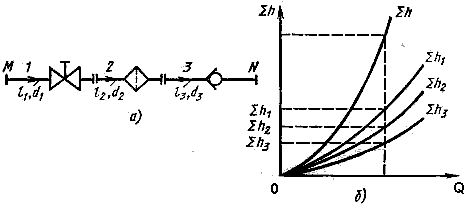
Рисунок 4. Последовательное соединение трубопроводов

 

Так как в рассматриваемом более общем случае скорости и на­чале М и конце N трубопровода различны, то выражение потребного напора для всего трубопровода М — N в отличие от формулы (1) должно содержать разность скоростных напоров в конце и начале трубопровода. Принимая a = 1, имеем

 

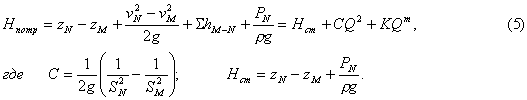
Параллельное соединение. Такое соединение нескольких простых трубопроводов (например 1, 2 и 3) между точками М и N показано на рисунке 5, а. Для простоты допустим, что трубопроводы располо­жены в горизонтальной плоскости.

Обозначим полные напоры в точках М и N соответственно через Н_M и H_N, расход в основной магистрали (т. е. до разветвления и после слияния) —. через Q, а в параллельных трубопроводах через Q₁, Q₂ и Q₃; суммарные потери напора в этих трубопроводах через Sh₁, Sh₂, Sh₃.

Прежде всего запишем следующее очевидное уравнение

Q₁ + Q₂ + Q₃ = Q; (6)

Затем выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N:

Sh₁=H_M-H_N;Sh₂=H_M-H_N; Sh₃=H_M-H_N;

Отсюда делаем следующий важный вывод:

Sh₁ = Sh₂ = Sh₃; (7)

т. е. потери напора в параллельных трубопроводах равны между со­бой. Их можно выразить в общем виде через соответствующие расходы следующим образом

Sh₁=K₁Q₁^m; Sh₂=K₂Q₂^m; Sh₃=K₃Q₃^m,

где К и m — определяются и зависимости от режима течения формулами (2) или (3).

Следовательно, в дополнение к уравнению (6) получаем на основании равенств (7) еще два уравнения:

K₁Q₁^m = K₂Q₂^m; (8) K₂Q₂^m = K₃Q₃^m. (9)

Система уравнений (6), (8) и (9) позволяет решать, например, следующую типичную задачу: даны расход в основной магистрали Q и все размеры трубопроводов; определить расходы в параллельных трубопроводах Q₁, Q₂ и Q₃.

 

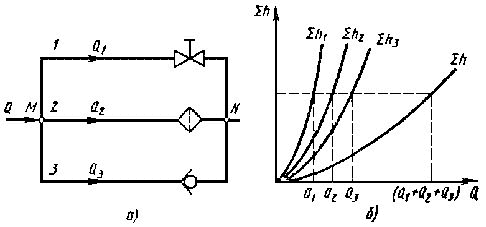
Рисунок 5. Параллельное соединение трубопроводов

 

Пользуясь выражениями (6) и (7), можно составить столько уравнений, сколько параллельных трубопроводов между точками М и N.

Из уравнений (6) и (7) вытекает следующее важное пра­вило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) ха­рактеристик этих трубопроводов при одинаковых ординатах (Sh). Пример такого построения дан на рисунке 5, б.

Изложенные соотношения и правила для параллельных трубопро­водов справедливы, разумеется, также в том случае, когда трубо­проводы 1, 2, 3 и т. д. (см. рисунок 6) не сходятся в одной точке N, а подают жидкость в разные места, но с одинаковыми давлениями и равными нивелирными высотами. Если же последнее условие не соблюдается, то рассматриваемые трубопроводы нельзя считать па­раллельными, а следует относить к разряду разветвленных трубопроводов.

Разветвленное соединение. Условимся называть разветвленным соединением совокупность нескольких простых трубопроводов, име­ющих одно общее сечение — место разветвления (или смыкания) труб.

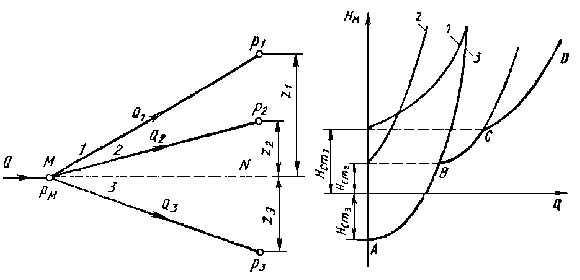
Рисунок 6. Разветвленный трубопровод

Рисунок 7. Построение кривой дляразветвленного трубопровода

 

Пусть основной трубопровод имеет разветвление в сечении М — М, от которого отходят, например, три трубы 1, 2 и 3 разных размеров, содержащие различные местные сопротивления (рисунок 6). Геометрические высоты Z₁, Z₂ и Z₃ конечных сечений и давления P₁, P₂ и Р₃ в них пусть будут также различными.

Найдем связь между давлением Р_м = Н_мrg в сечении М — М и расходами Q₁, Q₂ и Q₃ в трубопроводах, считая направление тече­ния в них заданным.

Так же как и для параллельных трубопроводов,

Q₁ + Q₂ + Q₃ = Q.

Записав уравнение Бернулли для сечения М — М и конечного сечения, например, первого трубопровода, получим (пренебрегая разностью скоростных высот)

Н_М=Z₁+P₁/(rg)+Sh₁.

Обозначая сумму двух первых членов в правой части уравнения через H_ст и выражая третий член через расход (как это делалось выше), получаем

Н_М=Н_ст1+K₁Q₁^m.

Аналогично для двух других трубопроводов можно записать

Н_М=Н_ст2+K₂Q₂^m; Н_М=Н_ст3+K₃Q₃^m.

Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q₁, Q₂, Q₃ и Н_М.

Основной задачей по расчету разветвленного трубопровода яв­ляется следующая: даны расход в точке М, все размеры ветвей (вклю­чая геометрические высоты z), давления в конечных сечениях и все местные сопротивления; определить расходы Q₁, Q₂ и Q₃, а также потребный напор Н_М = Н_потр. Возможны и другие варианты поста­новки задачи, решаемой на основе той же системы уравнений.

Построение кривой потребного напора для разветвленного тру­бопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопро­водов (рисунок 7) — сложением абсцисс (Q) при одинаковых ордина­тах (Нм). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3, а суммарная кривая, т. о. кривая потребного напора для всего разветвления, обозначена буквами ABCD. Из графика ясно, что условием подачи жидкости во все ветви является неравенство Нм > Н_ст1.

 

Сложные трубопроводы

Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рисунок 8, а) или с разветвлениями (рисунок 8, б).

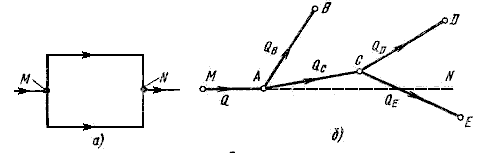
Рисунок 8. Схемы сложных трубопроводов

 

Рассмотрим разомкнутый сложный трубопровод с разветвлени­ями и с раздачей жидкости в конечных сечениях (точках) ветвей. Магистральный трубопровод разветвляется в точках А и С. Жид­кость подается к точкам (сечениям) В, D и Е с расходами Q_B, Q_D и Q_E.

Пусть известны размеры магистрали и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геомет­рические высоты конечных точек, отсчитываемые от плоскости М — N и избыточные давления в конечных точках P_B, P_D и P_E. В этом случае могут быть следующие основные задачи по расчету указанного трубопровода, соответствующие двум первым задачам, рассмотренным выше.

Задача 1. Дан расход Q в основной магистрали МA. Определить расходы в каждой ветви — Q_B, Q_D и Q_E, а также потребный напор в точке М: H_потр = Нм = P_М/rg.

Задача 2. Дан напор в точке М — H_м. Определить расход в маги­страли Q и расходы в каждой ветви.

Обе задачи решают на основе одной и той же системы уравне­ний, число которых на единицу больше числа конечных ветвей, а именно:

уравнение расходов

Q = Q_B + Q_D + Q_E,

равенства потребных напоров для ветвей CD и СЕ

Н_стD+K_CDQ_D^m = Н_стE + K_CEQ_E^m;

равенства потребных напоров для ветви АВ и сложного трубо­провода ACED

Н_стB+K_ABQ_B^m = Н_стD+K_CDQ_D^m +K_AC(Q_D+Q_E)­­^m;

выражение для потребного напора в точке М

H_M=P_M/rg=K_MAQ^m +H_стB+K_ABQ_B^m.

Здесь, как и выше, физический смысл статических напоров в конечных точках В, D и Е тот же, что и в формуле (1), а сопротив­ления ветвей К и показатели степени m определяются в зависимости от режима течения.

Расчет сложных трубопроводов часто выполняют графоаналитиче­ским способом, т. е. с применением кривых потребного напора или характеристик трубопроводов. Кривую потребного напора Н_потр для всего сложного трубопровода можно построить следующим образом:

1) сложный трубопровод разбить на ряд простых;

2) построить кривые потребных напоров для каждого из простых трубопроводов, причем для ветвей с конечной раздачей — с уче­том Н_ст, а для промежуточных участков (например, АС и МА) — без учета Н_ст;

3) сложить кривые потребных напоров для ветвей (и параллель­ных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;

4) полученную кривую сложить с характеристикой последова­тельно присоединенного трубопровода по соответствующему пра­вилу и т. д.

Таким образом, при расчете нужно идти от конечных точек сложного трубопровода к начальной его точке, т. е. против тече­ния жидкости.

Руководствуясь этим правилом, можно построить кривую потреб­ного напора для любого сложного трубопровода как при ламинарном, так и при турбулентном режиме течения. Выполнив описанное построение и получив график Н_потр = f(Q) можно с его помощью решать рассмотренные выше задачи 1 и 2 в различных вариантах. Кроме того, кривая потребного напора Н_потр необходима для расчета сложного трубопровода с насосной подачей.

Сложный кольцевой трубопровод представляет систему смежных замкнутых контуров — колец с отбором жидкости в узловых точках или с непрерывной раздачей ее на отдельных участках.

Рассмотрим простейший случай, когда трубопровод состоит из двух колец ОABC и ADEB (рисунок 9). Точка О является первич­ной точкой (узлом), из которой жидкость подается в сеть с расходом Q_о и где, следовательно, напор имеет наибольшее значение. В точ­ках А, В, С, D и Е происходит отбор жидкости с расходами, кото­рые обозначены соответственно Q_А, Q_B, Q_C, Q_D и Q_E.

Различные задачи расчета такого и более сложных кольцевых трубопроводов обычно решают аналитическим методом последовательных приближений или на ЭВМ с применением электроаналогий. При этом основываются на двух обязательных усло­виях, аналогичных требо­ваниям к расчету электрических сетей. Первое условие — баланс расходов, т. е. равенство притока и оттока жидкости для каждой узловой точки, что соответствует первому за­кону Кирхгофа в электротехнике (сила тока аналогична расходу). Второе условие — баланс напоров, т. о. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направле­нию движения часовой стрелки или против нее, что соответствует второму закону Кирхгофа (падение напряжения аналогично потере напора). Потери напора считаются положительными, если направ­ление подсчета совпадает с направлением движения жидкости, и отрицательными, если направление подсчета противоположно на­правлению движения жидкости.

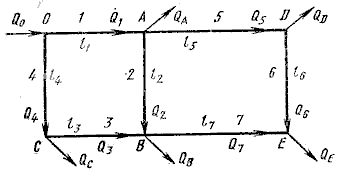
Рисунок 9. Схема сложного кольцевого трубопровода

 

Наиболее типичной для расчета сложных кольцевых трубопро­водов (сетей) является следующая задача, которую рассмотрим на примере показанной на рисунке 9 схемы двухкольцевого трубопро­вода. Даны максимальный напор в начальной точке (узле) 0 — Н_о, минимальный напор в наиболее удаленной точке Е — Н_Е, расходы во всех шести узлах (от Q_о до Q_Е) и длины семи участков 1— 7 (линий) (от l1 до l7). Требуется определить диаметры трубопроводов на всех семи участках.

Особенностью данной задачи, как и других задач расчета слож­ных кольцевых трубопроводов, является то, что неизвестными будут расходы на отдельных участках, в данном примере — расходы от Q1 до Q7 и напоры в четырех узлах А, В, С и D. Таким образом, всего имеем 18 неизвестных. Кроме того, неизвестно направление движения жидкости во втором участке (АВ).

Для нахождения этих неизвестных имеются следующие уравне­ния: шесть уравнений баланса расходов для шести узлов; два уравне­ния баланса напоров для двух колец и семь уравнений, связывающих потерю напора с расходом для каждого из семи участков. Таким образом, число уравнений (15) меньше числа неизвестных (18), по­этому при решении задачи в первом приближении надо задать диа­метры некоторых участков. Проще всего это сделать для участков 6 и 7, подающих жидкость к конечной точке Е, так как для них изве­стен суммарный расход (Q_Е = Q6+Q7).

Решение системы уравнений приходится выполнять неоднократно не только потому, что выбранные диаметры оказались неудачными, но и потому, что окончательно принятые диаметры труб на всех участках должны соответствовать ГОСТам.

Удобным расчетным приемом, применяемым при небольшом числе колец, является следующий. Сложный кольцевой трубопровод мыс­ленно разрывают в наиболее удаленной точке Е и в одной из точек участка 2 на два сложных разветвленных трубопровода OADE и ОСВЕ. Тогда расход на участке ОА будет a Q_о, а на участке ОС — (1 —a) Q_о. Значение коэффициента a можно приблизительно оце­нить, так как известны расходы Q_А и Q_D в одном из указанных трубопроводов и Q_C и Q_B — в другом; неизвестны лишь Q6 и Q7 из которых складывается Q_E.

Далее выполняют расчет каждого из двух сложных разветвлен­ных трубопроводов так, как это было описано выше. Если в этом расчете определяются диаметры, то при окончательном их выборе нужно соблюсти равенство потерь напора в линиях OADE и ОСВЕ.

 

 

Трубопроводы с насосной подачей жидкости

 

Выше рассмотрены, по существу, лишь отдельные участки простых и сложных трубопроводов, а не вся система подачи жидкости (кроме простейшей самотечной системы). В машиностроении, как уже отмечалось, основным способом подачи жидкости является при­нудительная подача насосом. Рассмотрим совместную работу трубо­провода с насосом и принцип расчета трубопровода с насосной пода­чей жидкости.

Трубопровод с насосной подачей может быть разомкнутым, т. е. таким, по которому жидкость перекачивается из одной емкости в другую (рисунок 10, а) или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рисунок 10, б).

Рассмотрим вначале разомкнутый трубопровод, по которому насос перекачивает жидкость, например из нижнего резервуара с давлением Р_о в другой резервуар (или в камеру) с давлением Р₃. Высота расположения оси насоса относительно нижнего уровня Н1 называется геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом, или линией всасывания. Высота расположения конеч­ного сечения трубопровода, или верхнего уровня жидкости Н2, называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным, или линией нагнетания.

Составим уравнение Бернулли для потока жидкости во всасы­вающем трубопроводе, т. е. для сечений 0—0 и 1—1 (принимая a = 1):

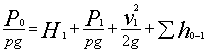(10)

Уравнение (10) является основным для расчета всасывающих трубопроводов. Оно показывает, что процесс всасывания, т. е. подъем

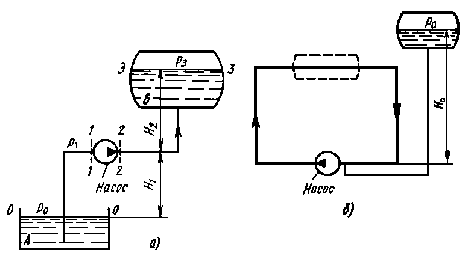
Рисунок 10. Трубопроводы с насосной подачей

жидкости на высоту Н1 сообщение ей кинетической энергии и пре­одоление всех гидравлических сопротивлений происходит за счет использования (с помощью насоса) давления Р_о. Так как это дав­ление обычно бывает весьма ограниченным, то расходовать его следует так, чтобы перед входом в насос остался некоторый запас давления Р₁, необходимый для его нормальной бескавитационной работы.

Возможны следующие задачи на расчет всасывающего трубопро­вода.

Задача 1. Даны все размеры и расход и требуется найти абсо­лютное давление перед входом в насос.

Решение этой задачи представляет собой поверочный расчет вса­сывающего трубопровода. Абсолютное давление Р₁, полученное по уравнению (10), сравнивают с тем, которое является мини­мально допустимым для данного случая.

Задача 2. Дано минимально допустимое абсолютное давление перед входом в насос Р₁ и требуется найти одну из следующих пре­дельно допустимых величин: Н_1mах, Q_max, d_min или P_0min.

Запишем уравнение Бернулли для движения жидкости по напор­ному трубопроводу, т. е. для сечений 2—2 и 3—3:

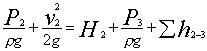(11)

Левая часть уравнения (11) представляет собой энергию жидкости на выходе из насоса, отнесенную к единице веса.

Аналогичная энергия жидкости перед входом в насос может быть вычислена по уравнению (11):

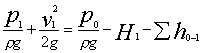
Найдем приращение энергии жидкости в насосе, т. е. определим ту энергию, которую приобретает, проходя через насос, каждая единица веса жидкости. Эта энергия сообщается жидкости насосом, поэтому она носит название напора, создаваемого насосом, и обозна­чается обычно H_нас.

Для нахождения Н_нас вычтем последнее уравнение из уравне­ния (11):

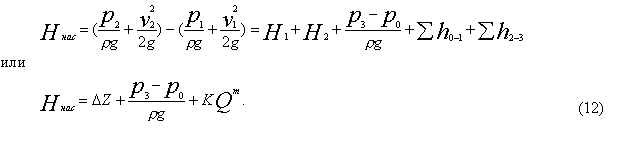
где D z — полная геометрическая высота подъема жидкости (см. рисунок 10, а); KQ^m — сумма гидравлических потерь во всасывающем и напорном трубопро­водах.

Если к действительной разности Dz уровней добавить разность пьезометрических высот (P₃ — P₀)/(r g), то можно рассматривать как бы увеличенную разность уровней

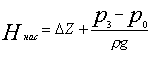
и формулу (12) переписать так:

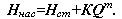(12’)

Очевидно, что

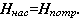(l3)

Это равенство можно распространить на все случаи устойчивой работы насоса, соединенного с трубопроводом, и сформулировать в виде следующего правила: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.

На равенстве (13) основывается метод расчета трубопрово­дов, питаемых насосом, который заключается в совместном построе­нии, в одном и том же масштабе и на одном графике двух кривых:

напора H_потр =f₁(Q) и характеристики насоса H_нас = f₂(Q) и в нахождении их точки пересечения (рисунок 11).

В дальнейшем будет достаточно подробно сказано о характеристиках насосов. Здесь же пока дадим лишь определение: характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рисунке 11 дано два варианта графика: а — для турбулентного режима течения в тру­бопроводе и центробежного насоса и б — для ламинарного режима и объемного насоса.

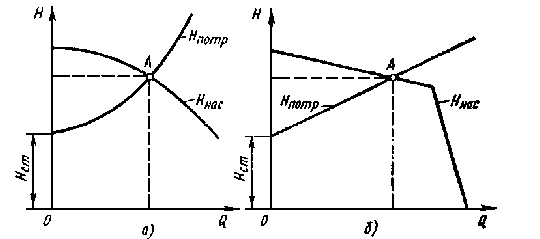
Рисунок 11. Графическое нахождение рабочей точки

В точке пересечении кривой потребного напора и характеристики насоса имеем равенство между потребным напором и напором, созда­ваемым насосом, т. е. равенство (13). Эта точка называется рабо­чей точкой, так как всегда реализуется режим работы насоса, ей соответствующий. Чтобы получить другую рабочую точку, необ­ходимо или изменить открытие регулировочного крана (вентиля, задвижки), т. е. изменить характеристику трубопровода, или изме­нить частоту вращения вала насоса.

Указанный расчетный прием для нахождения рабочей точки применим в том случае, когда частота вращения привода насоса не зависит от мощности, им потребляемой, т. е. от нагрузки на валу насоса. Это имеет место, например, при соединении насоса с электро­двигателем переменного тока или с иным двигателем, мощность кото­рого во много раз больше мощности насоса.

Для замкнутого трубопровода (рисунок 11, б) геометрическая высота подъема жидкости равна нулю (Dz = 0), следовательно, при v₁ = v₂:

Н_потр=S h=(P₂-P₁)/(r g),

т. е. между потребным напором и напором, создаваемым насосом, справедливо то же равенство.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Как можно классифицировать трубопроводы?

2. От каких факторов зависит сопротивление трубопроводов?

3. Как можно вычислить потери напора, используя обобщенные параметры?

4. Приведите уравнение напорной характеристики трубопровода в общем виде.

5. В чем заключается технико-экономический расчет трубопровода?