Глава 3. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Сила и плотность тока
Электрическим током называется упорядоченное движение электрических зарядов. Заряды, образующие электрический ток, называются носителями тока. Для существования электрического тока в проводящей среде необходимо наличие носителей тока и электрического поля внутри проводника. Под направлением тока понимается направление вектора плотности тока:
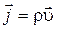 , (3.1)
, (3.1)
где 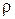 – объемная плотность носителей тока,
– объемная плотность носителей тока, 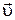 – скорость их упорядоченного движения.
– скорость их упорядоченного движения.
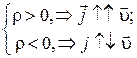
Заряд, переносимый через площадку 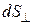 , перпендикулярную плотности тока
, перпендикулярную плотности тока 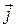 , за промежуток времени
, за промежуток времени 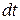 равен
равен
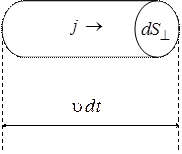
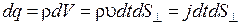 ,
,
отсюда
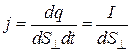 , (3.2)
, (3.2)
 где
где 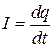 – сила тока, (количественная характеристика) равная величине заряда
– сила тока, (количественная характеристика) равная величине заряда 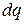 , переносимого через поверхность
, переносимого через поверхность 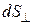 в единицу времени. Для постоянного тока
в единицу времени. Для постоянного тока
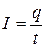 .
.
Элементарная сила тока, через поверхность 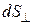 , из (3.2)
, из (3.2)
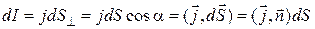 . (3.3)
. (3.3)
Зная вектор плотности тока 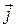 в каждой точке интересующей нас поверхности (
в каждой точке интересующей нас поверхности (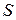 ), можно найти и силу тока через эту поверхность как поток вектора
), можно найти и силу тока через эту поверхность как поток вектора 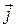 :
:
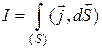 . (3.4)
. (3.4)
Сила тока – величина скалярная и алгебраическая.
Единица электрического тока в СИ: 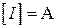 .
.
Единица электрического заряда в СИ: 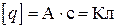 .
.
Единица плотности тока в СИ: 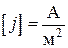 .
.
Уравнение непрерывности
Рассмотрим область 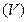 некоторой среды, в которой течет ток плотности
некоторой среды, в которой течет ток плотности 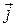 , и ограничим ее замкнутой поверхностью
, и ограничим ее замкнутой поверхностью 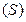 . Допустим, что заряд внутри области уменьшается с течением времени. Тогда скорость убывания заряда
. Допустим, что заряд внутри области уменьшается с течением времени. Тогда скорость убывания заряда 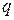 , содержащегося в объеме
, содержащегося в объеме 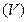 :
:
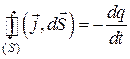 . (3.5)
. (3.5)
Представим:
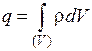 ,
,
тогда уравнение (3.5) можно записать в виде
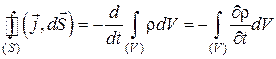 , (3.6)
, (3.6)
(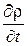 , так как
, так как 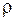 может зависеть не только от времени, но и от координат).
может зависеть не только от времени, но и от координат).
Преобразуем левую часть равенства (3.6) по теореме Остроградского- Гаусса, получим
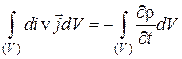 . (3.7)
. (3.7)
(3.7) – уравнение непрерывности в интегральной форме.
Равенство (3.7) должно выполняться при произвольном выборе 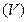 , по которому берутся интегралы. Это возможно лишь в том случае, если в каждой точке пространства объема
, по которому берутся интегралы. Это возможно лишь в том случае, если в каждой точке пространства объема 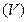 выполняется условие:
выполняется условие:
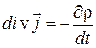 . (3.8)
. (3.8)
(3.8) – уравнение непрерывности в дифференциальной форме.
Физический смысл (3.8): в точках, которые являются источником вектора 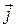 происходит убывание электрического заряда.
происходит убывание электрического заряда.
Для стационарного тока: 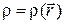 и
и 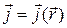 , следовательно
, следовательно 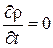 , и (3.8) примет вид
, и (3.8) примет вид
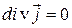 . (3.9)
. (3.9)
(3.9) – уравнение непрерывности для стационарного тока.
Таким образом, в случае стационарного (постоянного) тока вектор 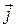 не имеет источников. Это означает, что линии тока замкнуты сами на себя.
не имеет источников. Это означает, что линии тока замкнуты сами на себя.
Электродвижущая сила
Под действием кулоновских сил взаимодействия, положительные носители тока в проводнике перемещаются от точек с большим потенциалом к точкам с меньшим потенциалом, а отрицательные носители движутся в обратном направлении. Это приводит к выравниванию потенциалов во всех точках проводника и исчезновению электрического тока. Поэтому поле кулоновских сил не может вызвать постоянный во времени процесс упорядоченного движения зарядов, т.е. постоянный ток. Следовательно, для существования постоянного тока в проводнике необходимо наличие сил не электростатического происхождения (сторонних сил), которые бы переносили положительные заряды против сил электрического поля в сторону возрастания потенциала, тем самым, поддерживая постоянную разность потенциалов на его концах. То есть, необходимо создать замкнутую проводящую цепь, в которой на носители тока действуют не только кулоновские, но также сторонние силы.
Природа сторонних сил может быть разной: химической, механической и т.д. Сторонние силы характеризуются электродвижущей силой (ЭДС), действующей в цепи или на некотором ее участке:
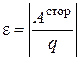 , (3.10)
, (3.10)
где 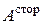 – работа сторонних сил по перемещению единичного положительного заряда
– работа сторонних сил по перемещению единичного положительного заряда 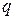 на рассматриваемом участке цепи.
на рассматриваемом участке цепи.
Добавочное поле сторонних сил создается источниками электрической энергии (батарейки, аккумуляторы, генераторы).
Закон Ома
Ом экспериментально установил закон: сила тока, текущего по однородному металлическому проводнику пропорциональна напряжению на проводнике, т.е. 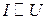 , или с учетом коэффициента пропорциональности
, или с учетом коэффициента пропорциональности 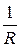 , получим
, получим
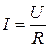 , (3.11)
, (3.11)
где 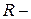 электрическое сопротивление проводника.
электрическое сопротивление проводника.
Для однородного проводника: 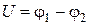 .
.
Величина сопротивления зависит от формы, размеров и материала проводника.
Для однородного цилиндрического проводника
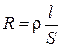 , (3.12)
, (3.12)
где 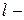 длина проводника;
длина проводника; 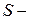 площадь его поперечного сечения;
площадь его поперечного сечения; 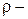 удельное электрическое сопротивление проводника.
удельное электрическое сопротивление проводника.
Величина, обратная удельному электрическому сопротивлению, называется удельной электрической проводимостью проводника
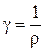 . (3.13)
. (3.13)
Найдем связь между плотностью тока 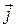 и полем
и полем 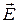 в локальной форме. Рассмотрим изотропный проводник, выделим в нем элементарный цилиндр объемом
в локальной форме. Рассмотрим изотропный проводник, выделим в нем элементарный цилиндр объемом 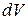 . Будем считать
. Будем считать 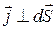 .
.
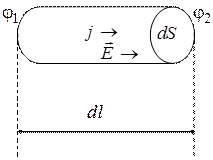
 Через поперечное сечение цилиндра течет ток силой
Через поперечное сечение цилиндра течет ток силой 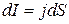 . Напряжение, между концами цилиндра
. Напряжение, между концами цилиндра 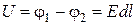 .
.
Сопротивление цилиндра 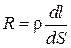 , тогда закон Ома для элементарного проводника в виде цилиндра в каждой точке среды:
, тогда закон Ома для элементарного проводника в виде цилиндра в каждой точке среды: 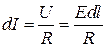 .
.
Из (3.3)
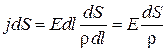 ,
,
или 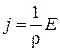 .
.
С учетом того, что 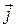 и
и 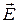 имеют одинаковое направление, можно написать
имеют одинаковое направление, можно написать
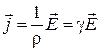 . (3.14)
. (3.14)
(3.14) – закон Ома в дифференциальной (локальной) форме.
Закон Ома для участка цепи
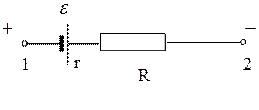 |
Участок цепи, содержащий (ЭДС) 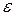 и
и
электрическое сопротивление, называется
неоднородным. Напряжение 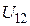 на таком участке равно:
на таком участке равно:
 (3.15)
(3.15)
Для неоднородного участка цепи закон Ома имеет вид:
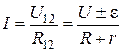 , (3.16)
, (3.16)
где 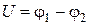 - разность потенциалов (напряжение) на концах участка;
- разность потенциалов (напряжение) на концах участка; 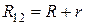 - электрическое сопротивление участка цепи;
- электрическое сопротивление участка цепи; 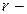 внутреннее сопротивление источника тока;
внутреннее сопротивление источника тока; 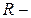 сопротивление проводника.
сопротивление проводника.
Знаки «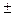 » отражают тот факт, что сторонние силы могут совершать как положительную, так и отрицательную работу на рассматриваемом участке цепи.
» отражают тот факт, что сторонние силы могут совершать как положительную, так и отрицательную работу на рассматриваемом участке цепи.
Участок цепи, на котором не действуют сторонние силы, называется однородным
 Закон Ома для однородного участка цепи имеет вид:
Закон Ома для однородного участка цепи имеет вид:
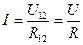 , (3.17)
, (3.17)
т.к. 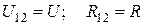 .
.
Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, 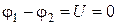 , и тогда закон Ома для такой цепи:
, и тогда закон Ома для такой цепи:

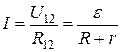 , (3.18)
, (3.18)
т.к. 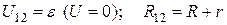 .
.
При последовательном соединении проводников: 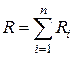 .
.
При параллельном соединении проводников: 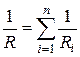 .
.
Единица электрического сопротивления в СИ: 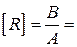 Ом.
Ом.
Единица напряжения (ЭДС) в СИ: 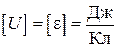 = В.
= В.
Закон Джоуля – Ленца
При прохождении тока по неподвижному проводнику, проводник нагревается. Количество выделившейся теплоты определяется законом Джоуля–Ленца. Для постоянного тока 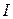 оно равно
оно равно
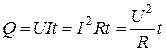 . (3.19)
. (3.19)
Элементарное количество теплоты
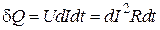 .
.
Если 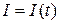 , или
, или 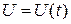 , то
, то
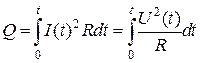 . (3.20)
. (3.20)
Для элементарного цилиндра 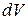 (см. закон Ома в дифференциальной форме), тепловая мощность на этом участке равна
(см. закон Ома в дифференциальной форме), тепловая мощность на этом участке равна
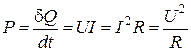 (3.21)
(3.21)
Удельная тепловая мощность
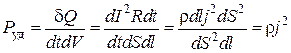 .
.
Используя закон Ома в дифференциальной форме: 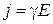 , получим
, получим
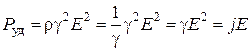 . (3.22)
. (3.22)
(3.22) – закон Джоуля-Ленца в дифференциальной (локальной) форме.
Единица тепловой мощности в СИ: 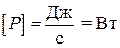 .
.