Интегральная функция распределения непрерывной случайной величины
Непрерывной случайной величиной 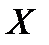 называется такая величина, возможные значения которой непрерывно заполняют некоторый интервал числовой оси (конечный или бесконечный). Приведем примеры непрерывных случайных величин.
называется такая величина, возможные значения которой непрерывно заполняют некоторый интервал числовой оси (конечный или бесконечный). Приведем примеры непрерывных случайных величин.
1. Случайное отклонение точки попадания снаряда от цели.
2. Ошибка при измерении.
3. Время безотказной работы прибора.
Поскольку число возможных значений непрерывной случайной величины бесконечно, для нее невозможно написать закон распределения в такой же форме, как для дискретной случайной величины. Поэтому целесообразно дать общий способ задания любых типов случайных величин. С этой целью вводят интегральную функцию распределения.
Пусть 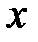 - действительное число. Вероятность события, состоящего в том, что случайная величина
- действительное число. Вероятность события, состоящего в том, что случайная величина 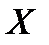 примет значение, меньшее
примет значение, меньшее 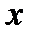 , обозначим через
, обозначим через 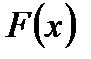 . Если
. Если 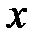 будет изменяться, то вообще говоря, будет изменяться и
будет изменяться, то вообще говоря, будет изменяться и 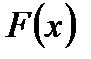 , то есть
, то есть 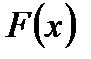 является функцией от
является функцией от 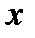 .
.
Интегральной функцией распределения непрерывнойслучайной величины 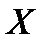 называют функцию
называют функцию 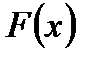 , определяющую для каждого значения
, определяющую для каждого значения 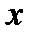 вероятность того, что случайная величина
вероятность того, что случайная величина 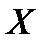 примет значение, меньше
примет значение, меньше 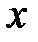 :
:
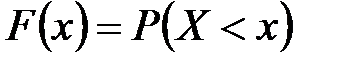 .
.
Геометрически это равенство можно истолковать так: 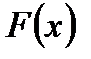 есть вероятность того, что случайная величина (5.1)
есть вероятность того, что случайная величина (5.1) 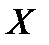 примет значение, которое изображается на числовой оси точкой, лежащей левее точки
примет значение, которое изображается на числовой оси точкой, лежащей левее точки 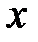 . Термин “интегральная функция распределения” иногда укорачивают и говорят: “интегральная функция” или “функция распределения”. Из определения интегральной функции следует, что она существует для всех случайных величин: как для дискретных, так и для непрерывных.
. Термин “интегральная функция распределения” иногда укорачивают и говорят: “интегральная функция” или “функция распределения”. Из определения интегральной функции следует, что она существует для всех случайных величин: как для дискретных, так и для непрерывных.
Свойства интегральной функции.
1. Значение интегральной функции принадлежат отрезку 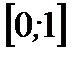 ,
,

Доказательство. Свойство вытекает из определения интегральной функции, поскольку вероятность любого события заключена в промежутке от 0 до 1.
2. 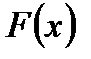 - неубывающая функция, т.е.
- неубывающая функция, т.е. 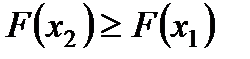 , если
, если 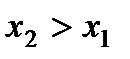 .
.
Доказательство. Пусть 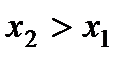 . Событие, состоящее в том, что
. Событие, состоящее в том, что 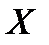 примет значение, меньшее
примет значение, меньшее 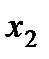 , можно подразделить на следующие два несовместных события:
, можно подразделить на следующие два несовместных события:
1) 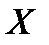 примет значение, меньшее
примет значение, меньшее 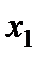 , с вероятностью
, с вероятностью 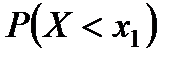 ;
;
2) 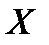 примет значение, удовлетворяющее неравенству
примет значение, удовлетворяющее неравенству 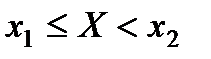 , с вероятностью
, с вероятностью 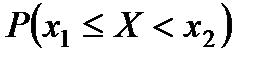 .
.
По теоремам о вероятности суммы и произведения независимых событий имеем
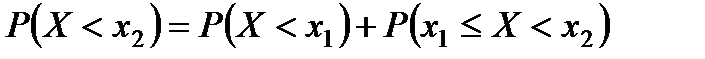 . Отсюда
. Отсюда
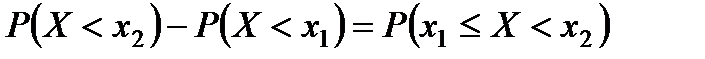
или
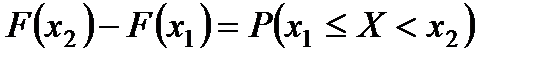
| (*) |
Так как любая вероятность есть число неотрицательное, то 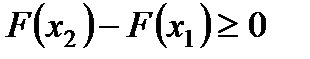 , или
, или 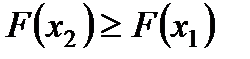 , что и требовалось доказать.
, что и требовалось доказать.
Следствие 1. Вероятность того, что непрерывная случайная величина 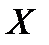 примет одно определенное значение, равна нулю, т.е.
примет одно определенное значение, равна нулю, т.е. 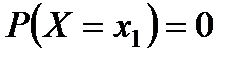 .
.
Действительно, положив в формуле (*) 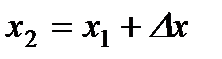 , получим
, получим
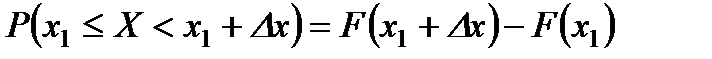 .
.
Устремим  к нулю. Так как
к нулю. Так как 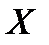 - непрерывная случайная величина, то функция
- непрерывная случайная величина, то функция 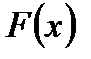 непрерывна. Значит, разность
непрерывна. Значит, разность 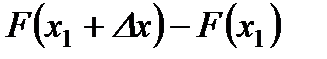 будет стремиться к нулю, следовательно,
будет стремиться к нулю, следовательно, 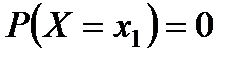 .
.
Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый.
Этот факт полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером.
Следствие 2. Вероятность того, что случайная величина примет значение, заключенное в интервале 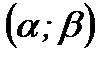 , равна приращению интегральной функции на этом интервале:
, равна приращению интегральной функции на этом интервале:
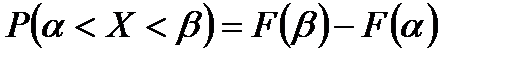 .
.
Это важное следствие вытекает из формулы (*), если положить 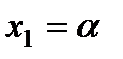 ,
, 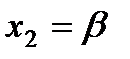 и учесть, что
и учесть, что 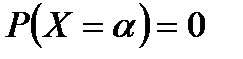 .
.
Замечание. В дальнейшем мы будем обращать внимание, строгие или нестрогие неравенства записаны для случайной величины то ли в самом задании интегральной функции, то ли в формуле для вычисления вероятности попадания в интервал.
3. Если возможные значения случайной величины принадлежат интервалу 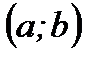 , то
, то
1) 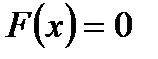 при
при 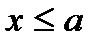 ;
;
2) 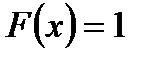 при
при 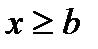 .
.
Доказательство.
1) Пусть 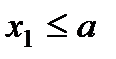 . Тогда событие
. Тогда событие 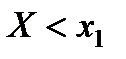 невозможно и, следовательно, вероятность его равна нулю.
невозможно и, следовательно, вероятность его равна нулю.
2) Пусть 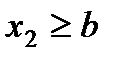 . Тогда событие
. Тогда событие 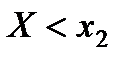 достоверно и, следовательно, его вероятность равна единице.
достоверно и, следовательно, его вероятность равна единице.
Следствие 3. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
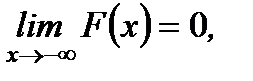
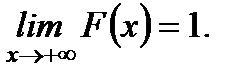
Из рассмотренных свойств интегральной функции распределения непрерывной случайной величины (7.1) следует, что ее график имеет вид, изображенный на рисунках 7.1. (а, б, в).
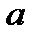
|
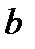
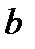
|
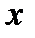
|
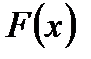
|
| а) |
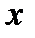
|
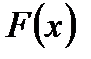
|
| б) |
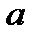
|
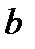
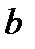
|
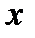
|
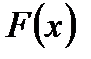
|
| в) |
| Рис. 7.1 |
В случае а) возможные значения непрерывной случайной величины принадлежат интервалу 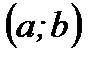 . В случае б) возможные значения непрерывной случайной величины расположены на всей числовой оси. А на рисунке 7.1. в) приведен график дискретной случайной величины (5.2).
. В случае б) возможные значения непрерывной случайной величины расположены на всей числовой оси. А на рисунке 7.1. в) приведен график дискретной случайной величины (5.2).
Обращаем внимание читателя на тот факт, что график интегральной функции для непрерывной случайной величины – непрерывная кривая, а для дискретной случайной величины (5.2) график имеет ступенчатый вид. Убедимся в этом на приведенных ниже примерах.
Пример 1. Дан закон распределения дискретной случайной величины (5.3)
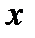
| ||||
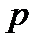
| 0,2 | 0,4 | 0,3 | 0,1 |
Записать интегральную функцию этой случайной величины и построить ее график.
Решение. Пусть  . Вероятность того, что случайная величина
. Вероятность того, что случайная величина 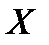 примет значение, меньшее
примет значение, меньшее 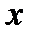 , равно 0, т.к. на интервале
, равно 0, т.к. на интервале 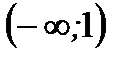 возможных значений случайной величины нет.
возможных значений случайной величины нет.
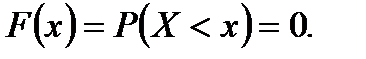
Пусть 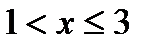 . Событие
. Событие 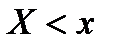 заключается в том, что случайная величина
заключается в том, что случайная величина 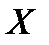 примет только одно из своих возможных значений, а именно
примет только одно из своих возможных значений, а именно 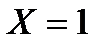 . Вероятность этого события
. Вероятность этого события 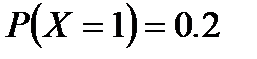 , значит,
, значит,
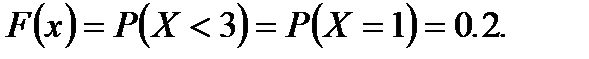
Пусть 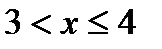 . Вероятность того, что случайная величина
. Вероятность того, что случайная величина  примет значение, меньшее
примет значение, меньшее  , будет состоять из суммы двух вероятностей:
, будет состоять из суммы двух вероятностей: 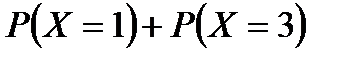 . Так как случайная величина может принять только одно из своих возможных значений, то применима теоремам о вероятности суммы и произведения независимых событий (1.6)
. Так как случайная величина может принять только одно из своих возможных значений, то применима теоремам о вероятности суммы и произведения независимых событий (1.6)
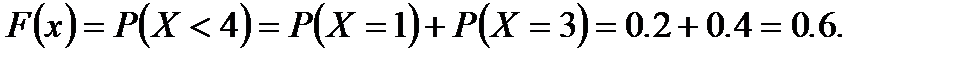
Аналогично, пусть 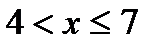 .
.
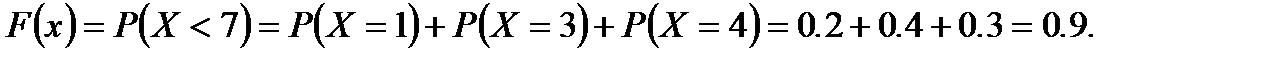
И, наконец, пусть 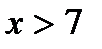 .
. 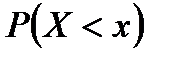 - это вероятность достоверного события, т.к. все возможные значения случайной величины лежат левее точки
- это вероятность достоверного события, т.к. все возможные значения случайной величины лежат левее точки 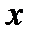 .
.
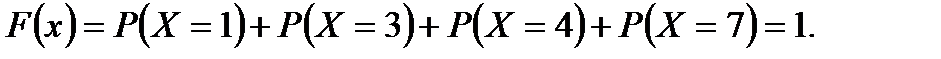
| 0,9 0,6 0,2 |
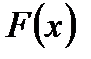
|
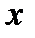
|
