Рассмотрим общую формулу степенной средней величины.
Осреднённый признак – тот признак, по которому находится средняя величина, обозначается 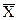 .
.
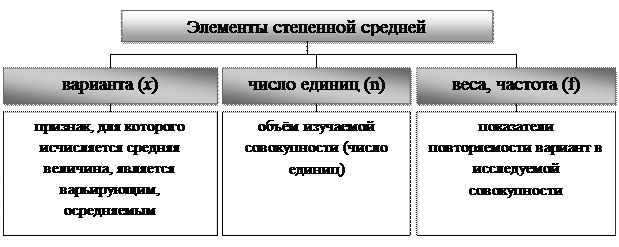
В общем виде структура степенной средней состоит из следующих элементов:
1). Варианты – индивидуальные значения признака, по которым рассчитывается средняя, величина усредняемого признака у каждой единицы совокупности, обозначается 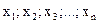 .
.
2). Объём статистической совокупности – число единиц в изучаемой совокупности, объём усредняемого признака, количество вариант, обозначается n.
3). Частота (вес) – показатель повторяемости вариант в статистической совокупности, обозначается f.
4). Объём частот определяется через произведение варианты и частоты, обозначается как 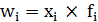 , i=1, 2, …, n.
, i=1, 2, …, n.
5). Частость (доля, удельный вес) – отношение частоты повторения индивидуального значения признака к сумме всех частот: 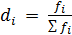
6). Степень средней, обозначается k.
Степенные средние, в зависимости от представления отдельных величин, могут быть простыми и взвешенными.
Простая степенная средняя рассчитывается при наличии двух и более статистических величин, расположенных в произвольном порядке. Общая формула простой средней величины имеет вид:
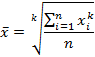
Взвешенная степенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
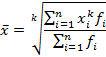
В зависимости от показателя степени k выделяют различные виды степенной средней:
1) при k=-1 – средняя гармоническая;
2) при k=0 – средняя геометрическая;
3) при k=1 – средняя арифметическая;
4) при k=2 – средняя квадратическая;
5) при k=3 – средняя кубическая;
6) при k=4 – средняя биквадратическая.
1). Средняя арифметическая (k=1) является самым распространённым видом средних величин. Она исчисляется в тех случаях, когда объём варьирующего признака для всей совокупности образуется как сумма значений признака отдельных её единиц.
|
|
Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, делённой на число этих значений:
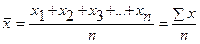 .
.
Средняя арифметическая как величина теоретическая может принимать такое числовое значение, которое не встречается в представленной совокупности индивидуальных значений признаков.
Средняя арифметическая взвешенная учитывает частоту повторяемости варианты:
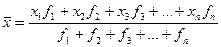 ,
, 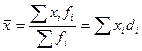 .
.
Средняя арифметическая взвешенная зависит не только от индивидуальных значений признака, но и от соотношения их частот (весов). Чем большие веса имеют малые значения вариант, тем меньше величина средней, и наоборот.
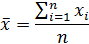
| средняя арифметическая простая |
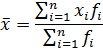
| средняя арифметическая взвешенная |
Средняя арифметическая обладает некоторыми математическими свойствами:
| Свойство | Формула расчёта |
| Основные | |
| 1. Средняя от постоянной величины равна ей самой | 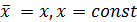
|
| 2. Сумма отклонений индивидуальных значений признака (вариант) от средней арифметической равна нолю (нулевое свойство) | 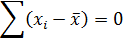 или
или
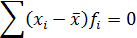
|
| 3. Сумма квадратов отклонений индивидуальных значений признака (вариант) от средней арифметической есть наименьшее число (минимальное свойство) | 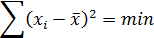 или
или
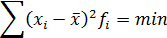
|
| Производные (расчётные) | |
| 4. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты | 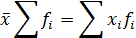
|
| 5. Увеличение (уменьшение) каждой варианты на какое-либо произвольное число увеличивает (уменьшает) среднюю на то же число | 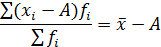 или
или
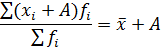
|
| 6. Умножение (деление) каждой варианты на какое-либо произвольное число увеличивает (уменьшает) среднюю во столько же раз | 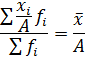 или
или
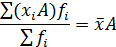
|
| 7. Изменение всех частот (весов) в одно и то же число раз не изменяет величину средней | 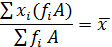
|
| 8. Общий множитель вариант может быть вынесен за знак средней | 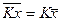
|
| 9. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних | 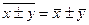
|
|
|
Пример 1.1.
5 рабочих токарей делают одинаковые детали за смену: первый – 12, второй – 9, третий – 11, четвертый – 13, пятый – 15.
Определить среднюю производительность труда рабочих.
Исходные данные не повторяются, поэтому используем простую среднюю арифметическую величину:
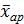 =
= 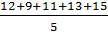 =
= 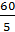 = 12.
= 12.
Пример 1.2.
Определить среднюю грузоподъёмность одного крана, если имеется:
Число кранов (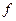 ) )
| Грузоподъёмность, тонн (х) |
| Итого 10 |
Для сгруппированных данных применяем среднюю арифметическую взвешенную:
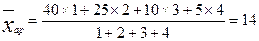 тонн.
тонн.
Определение средней арифметической по данным интервального вариационного ряда происходит следующим образом: для каждого ряда определяется среднее значение интервала как полусумма его нижнего и верхнего значения вариант, а далее расчёт ведётся по формуле средней арифметической взвешенной.
Пример 1.3.
Распределение рабочих цеха по производительности
| Производительность, шт. | Среднее значение xi | Количество рабочих fi |
| 0-5 | 2,5 | |
| 5-10 | 7,5 | |
| 10-15 | 12,5 | |
| 15-20 | 17,5 | |
| 20 и более | 22,5 | |
| Всего: |
|
|
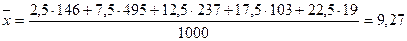 (лет)
(лет)
В практике экономической статистики иногда приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним). В таких случаях за варианты (х) принимаются групповые или частные средние, на основании которых исчисляется общая средняя как обычная средняя арифметическая взвешенная.
Если статистические данные представлены на определённый момент времени (дату) и интервалы времени между датами равны, то расчёт средней ведут по формуле средней хронологической простой, которая является частным случаем средней арифметической простой:
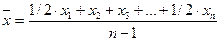
Пример 1.4.
Дан моментный ряд:
| 1.01 | 1.02 | 1.03 | 1.04 | |
| Численность рабочих, чел. |
Определить среднюю численность рабочих за четыре месяца.
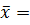
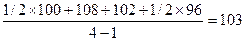 чел.
чел.
2). Средняя гармоническая (k =-1) вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины: 1/x1, 1/x2, …,1/xn. Это величина, обратная среднеарифметической. Она применяется, когда известны отдельные значения варьирующего признака и вся совокупность признаков, а частоты неизвестны.
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчётов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т. е. w = xf).
Существует два вида среднегармонической.
Средняя гармоническаяпростая определяется:
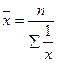
К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трём, четырём и т. д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.
Пример 2.1.
Скорость по течению реки 60 км/ч., против течения – 40 км/ч. Определить среднюю скорость движения.
Весь путь S=1, но тем не менее путь проходят дважды, то S=2, V1=60 км/ч., V2=40 км/ч., тогда средняя скорость движения:
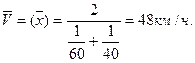
Средняя гармоническаявзвешеннаяопределяется:
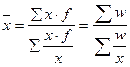
Пример 2.2.
Имеются данные о валовом сборе и урожайности зерновых культур по трём сельскохозяйственным предприятиям:
| С/х предприятие | Валовый сбор, ц | Урожайность, ц/га |
| w | 
|
Определить среднюю урожайность.
Валовый сбор = урожайность 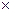 площадь.
площадь.
Частота – площадь посевов.
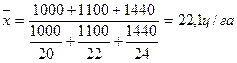
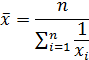
| средняя гармоническая простая |
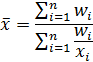
| средняя гармоническая взвешенная |
Средние арифметическая и гармоническая взвешенные часто применяются для осреднения относительных величин интенсивности, т. е. показателей, имеющих дробную размерность. При этом соблюдаются следующие правила:
1. Если имеются дополнительные данные по числителю дробной размерности, то применяется средняя гармоническая.
2. Если имеются дополнительные данные по знаменателю дробной размерности, то применяется средняя арифметическая.
3. Если неясно, к числителю или знаменателю относятся дополнительные данные, то поочередно применяются средняя гармоническая и арифметическая, а затем определяется средняя между ними величина.
Для иллюстрации правил решим задачу: 4 фирмы выпускают одинаковую продукцию при себестоимостях в руб./ед.: 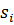 = 5, 3, 4, 6, а доли фирм равны соответственно
= 5, 3, 4, 6, а доли фирм равны соответственно 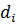 = 0,3; 0,2; 0,4; 0,1. Определить среднюю себестоимость продукции.
= 0,3; 0,2; 0,4; 0,1. Определить среднюю себестоимость продукции.
Для решения примера используем вышеизложенные правила.
1. Если доли фирм относятся к текущим затратам (числитель показателя себестоимости), то её среднее значение определяем по формуле как среднюю гармоническую величину:
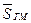 = 1/ (0,3/5 + 0,2/3 + 0,4/4 + 0,1/6) = 4,1 (руб./ед.)
= 1/ (0,3/5 + 0,2/3 + 0,4/4 + 0,1/6) = 4,1 (руб./ед.)
2. Если доли фирм относятся к количеству выпущенной продукции (знаменатель показателя себестоимости), то её среднее значение находим по формуле как среднюю арифметическую величину:
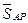 = 5*0,3 + 3*0,2 + 4*0,4 + 6*0,1 = 4,3 (руб./ед.)
= 5*0,3 + 3*0,2 + 4*0,4 + 6*0,1 = 4,3 (руб./ед.)
3. Если не сказано, к чему относятся доли фирм, то в дополнение к выполненным расчетам определяем среднюю себестоимость как простую среднюю величину из полученных результатов. То есть 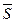 = (
= (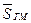 +
+ 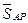 )/2 = 4,2 (руб./ед.)
)/2 = 4,2 (руб./ед.)
Таким путём рассчитываются средние значения и других показателей с дробной размерностью.
3). Средняя геометрическая (k =0) используется в тех случаях, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин.
На практике используется для вычисления среднего коэффициента роста в рядах динамики.
Формула средней геометрической простой
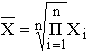
используется чаще всего при расчёте среднего значения по индивидуальным относительным величинам динамики.
При неравенстве отрезков времени при определении динамики используются частоты f, и расчёт ведётся по формуле средней геометрической взвешенной:
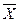 =
= 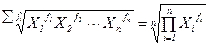
Средняя геометрическая применяется, если задана последовательность цепных относительных величин динамики, указывающих, например, на рост объёма производства по сравнению с уровнем предыдущего года.
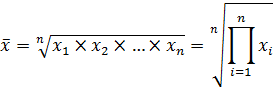
| средняя геометрическая простая |
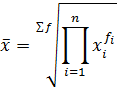
| средняя геометрическая взвешенная |
Свойства средней геометрической:
1. При замене отдельных значений усредняемых величин xi их средней геометрической общее произведение не изменится:
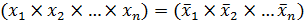
2. Для средней геометрической имеет место следующие равенство:
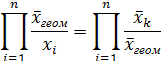
3. Если значения xi представляют собой отношения взаимно соответствующих членов двух параллельных распределений, то средняя геометрическая значений xi равна отношению геометрических средних этих распределений. Иначе говоря, если xi = yi/zi, то справедливо равенство:
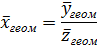
4. Средняя геометрическая равна нулю, если хотя бы один элемент усредняемой совокупности значений xi равен нулю. Средняя геометрическая может оказаться мнимой величиной, если среди значений xi встречаются отрицательные величины.
4). Средняя квадратическая (k =2) применяется в тех случаях, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.
На практике используется, например, при расчёте средних диаметров труб, стволов деревьев, а также для вычисления среднего квадратического отклонения и других показателей вариации.
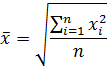
| средняя квадратическся простая |
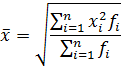
| средняя квадратическся взвешенная |
Таблица 2.1. Виды средних степенных величин
| k | Наименование средней | Формула средней | Когда используется |
| Средняя арифметическая простая (невзвешенная) | 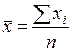 , где xi – i-й вариант осредняемого признака ( , где xi – i-й вариант осредняемого признака (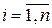 ); n – число вариант ); n – число вариант
| Используется, когда расчёт осуществляется по несгруппированным данным | |
| Средняя арифметическая взвешенная | 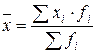 , где fi – частота повторяемости i-го варианта , где fi – частота повторяемости i-го варианта
| Используется, когда данные представлены в виде рядов распределения или группировок | |
| -1 | Средняя гармоническая взвешенная | 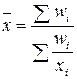 , где , где 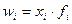 . .
| Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов |
| -1 | Средняя гармоническая невзвешенная | 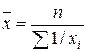
| Используется в случае, когда веса равны |
| Средняя геометрическая невзвешенная | 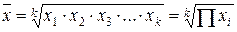
| Используется в анализе динамики для определения среднего темпа роста | |
| Средняя геометрическая взвешенная | 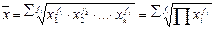
| ||
| Средняя квадратическая невзвешенная | 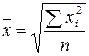
| Используется при расчете показателей вариации | |
| Средняя квадратическая взвешенная | 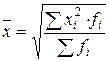
|
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних (впервые сформулировал профессор А. Я. Боярский): с ростом показателя степени k в общей формуле увеличивается и соответствующее значение средней величины:
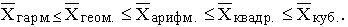
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.