Измерения и обработка результатов измерений

Измерение физических величин и получение их числовых значений являются непосредственной задачей большинства физических экспери­ментов. При измерениях значение физической величины выражается в виде числа, которое указывает, во сколько раз измеренная величи­на больше (или меньше) другой величины, значение которой принято за единицу. Полученные в результате измерений числовые значения различных величин, например, времени, пути, скорости и т. д., могут зависеть друг от друга. Физика устанавливает связь между такими величинами и выражает ее в виде формул, которые показывают, как числовые значения одних величин могут быть найдены по числовым значениям других.

Получение надежных числовых значений не является простой за­дачей из-за погрешностей, неизбежно возникающих при измерениях. Мы рассмотрим эти погрешности, а также методы, применяемые при обработке результатов измерений. Владение этими методами нужно для того, чтобы научиться получать из совокупности измерений наи­более близкие к истине результаты, вовремя заметить несоответствия и ошибки, разумно организовать сами измерения и правильно оценить точность полученных значений.

Измерения и их погрешности. Измерения делятся на прямые и косвенные.

Прямые измерения производятся с помощью приборов, которые из­меряют непосредственно саму исследуемую величину. Так, массу тела можно найти с помощью весов, длину измерить линейкой, а время — секундомером.

К косвенным относятся измерения таких физических величин, для нахождения которых необходимо использовать связь в виде формулы с другими, непосредственно измеряемыми величинами, например, нахо­ждение объема тела по его линейным размерам, нахождение плотности тела по измеренным массе и объему, расчет сопротивления проводника по показаниям вольтметра и амперметра.

Качество измерений определяется их точностью. При прямых изме­рениях точность опытов устанавливается из анализа точности метода и прибора, а также из повторяемости результатов измерений. Точность косвенных измерений зависит как от надежности используемых для расчета данных, так и от структуры формул, связывающих эти дан­ные с искомой величиной.

Точность измерений характеризуется их погрешностями. Абсолют­ной погрешностью измерений называют разность между найденным на опыте и истинным значением физической величины. Обозначая абсолютную погрешность измерения величины х символом Δ х, получим

 

(1)

 

Кроме абсолютной погрешности Δ х часто бывает важно знать относительную погрешность ε _х измерений, которая равна отношению абсолютной погрешности к значению измеряемой величины:

. (2)

Качество измерений обычно определяется именно относительной, а не абсолютной погрешностью. Одна и та же погрешность в 1 мм при измерении длины комнаты не играет роли, при измерении стола мо­жет быть существенна, а при определении диаметра болта совершенно недопустима. Это происходит потому, что относительная погрешность измерений в первом случае составляет ~2 · 10^-4, во втором ~10^-3, ав третьем может составлять десяток процентов и более. Вместо того что­бы говорить об абсолютной и относительной погрешности измерений, часто говорят об абсолютной и относительной ошибке. Между терми­нами «погрешность» и «ошибка» нет никакого различия, и мы будем пользоваться ими обоими.

Согласно (1) и (2), для того чтобы найти абсолютную и относи­тельную погрешности измерения, нужно знать не только измеренное, но и истинное значение интересующей нас величины. Но если истинное значение известно, то незачем производить измерения. Цель измере­ний всегда состоит в том, чтобы узнать неизвестное заранее значение физической величины и найти если не истинное ее значение, то хо­тя бы значение достаточно мало от него отличающееся. Что касается погрешностей, то, строго говоря, они не вычисляются, а оцениваются. При оценках учитываются условия проведения эксперимента, точность методики, качество приборов и ряд других факторов.

 

Систематические и случайные погрешности. Говоря опогреш­ностях измерений, необходимо прежде всего упомянуть о грубых по­грешностях (промахах), возникших вследствие недосмотра эксперимен­татора или неисправности аппаратуры. Грубых ошибок следует избе­гать. Если установлено, что они произошли, соответствующие измере­ния нужно отбросить.

Не связанные с грубыми ошибками погрешности опыта делятся на систематические и случайные.

Систематические погрешности сохраняют свою величину и знак во время эксперимента. Они могут быть связаны с ошибками прибо­ров (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического винта, неравные плечи весов) и с самой постановкой опыта, например, при взвешивании тела малой плотности без учета выталкивающей архимедовой силы, которая си­стематически занижает вес тела. Систематические погрешности опыта могут быть изучены и учтены путем внесения поправок в результаты измерений. Если систематическая погрешность опыта слишком вели­ка, то обычно оказывается проще использовать новые, более точные приборы, чем исследовать погрешность старых.

Случайные погрешности меняют величину и знак от опыта к опы­ту. Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а «пляшут» вокруг некоторого среднего значения.

Случайные погрешности могут быть связаны, например, с сухим трением (из-за которого стрелка прибора вместо того, чтобы останавли­ваться в правильном положении, «застревает» вблизи него), с люфтом в механических приспособлениях, с тряской, которую в городских усло­виях трудно исключить, с несовершенством объекта измерений (напри­мер, при измерении диаметра проволоки, которая из-за случайных при­чин, возникающих при изготовлении, имеет не вполне круглое сечение) или с особенностями самой измеряемой величины. Примером в послед­нем случае может быть число космических частиц, регистрируемых счетчиком за 1 минуту. Повторяя измерения, найдем, что в разных опытах получаются разные числа, хотя и не слишком отличающиеся друг от друга, колеблющиеся около некоторого среднего значения.

Случайные погрешности эксперимента исследуются путем сравне­ния результатов, полученных при нескольких измерениях, проведен­ных в одинаковых условиях. Если при двух-трех измерениях резуль­таты совпали, то на этом следует остановиться. Если они расходятся, нужно попытаться понять причину расхождения и устранить ее. Если устранить причину не удается, следует произвести 10-12 измерений и, записав все результаты, обработать их в соответствии с полученной закономерностью разброса величин.

Различие между систематическими и случайными погрешностями не является абсолютным и связано с постановкой опыта. Например, производя измерение тока не одним, а несколькими одинаковыми ам­перметрами, мы превращаем систематическую ошибку, связанную с неточностью шкалы, в случайную ошибку, величина и знак которой от того, какой поставлен амперметр в данном опыте. Однако во всяком опыте — при заданной его постановке — различие между си­стематическими и случайными погрешностями всегда можно и нужно устанавливать с полной определенностью.

Систематические погрешности. К систематическим погрешностям относятся, как уже отмечалось, такие, которые обязаны своим проис­хождением действию неизменных по своей величине и направлению факторов. Теоретически рассуждая, систематические погрешности все­гда могут быть учтены и, следовательно, исключены. Практически эта задача является делом трудным и требует большого искусства экспе­риментатора.

Оценку систематических погрешностей экспериментатор проводит, анализируя особенности методики, паспортную точность прибора и проводя контрольные опыты. В учебном практикуме учет систематиче­ских ошибок ограничивается, как правило, лишь случаем инструмен­тальных погрешностей. Остановимся на наиболее часто встречающих­ся случаях.

Систематические погрешности стрелочных электроизмерительных приборов (амперметров, вольтметров, потенциометров и т. п.) опреде­ляются их классом точности, который выражает абсолютную погреш­ность прибора в процентах от максимального значения включенной шкалы. Пусть на шкале вольтметра с диапазоном показаний от 0 до10 В в кружке стоит цифра 1. Эта цифра показывает, что класс точ­ности вольтметра 1 и предел его допустимой погрешности равен 1%от максимального значения включенной шкалы, т. е. равен ±0,1 В. Кро­ме того, надо иметь в виду, что наносить деления на шкале принято с таким интервалом, чтобы величина абсолютной погрешности прибора не превышала половины цены деления шкалы.

Класс точности стрелочных электроизмерительных приборов (как и полцены деления шкалы) определяет максимальную (предельную) абсолютную погрешность, величина которой не меняется вдоль всей шкалы. Относительная же погрешность при этом резко меняется, по­этому приборы обеспечивают лучшую точность при отклонении стрел­ки почти на всю шкалу. Отсюда следует рекомендация: выбирать при­бор (или шкалу многошкального прибора) так, чтобы стрелка прибора при измерениях находилась во второй половине шкалы.

В последнее время широко используются цифровые универсальные приборы, в том числе и электроизмерительные, отличающиеся высо­кой точностью и многоцелевым назначением. В отличие от стрелочных приборов систематические погрешности цифровых электроизмеритель­ных приборов оцениваются по формулам, приводимым в инструкциях по эксплуатации. Так, например, значение относительной погрешности в процентах универсального цифрового вольтметра В7-34, работающе­го на включенном пределе 1 В, оценивается по формуле

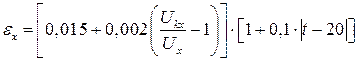, (3)

где - конечное значение предела измерения, В,

U_x - значение измеряемой величины, В,

t - температура, °С.

В случае измерения этим прибором постоянного напряжения вели­чиной 0,5 В при температуре окружающей среды t = 30 °С значение предела допустимой погрешности равняется:

 

,

что составляет ±0,00017 В от измеряемой величины 0,5 В.

При изменении предела измерений прибора (на 100 или 1000 В) или вида измерений (ток, сопротивление) структура формулы не изменяет­ся, меняются только числа, входящие в формулу. Точность вольтметра В7-34 обеспечивается при соблюдении следующих условий: окружаю­щая температура 5-40 °С, относительная влажность воздуха до 95% при 30 °С, напряжение питающей сети ~220 ± 22 В.

Несколько слов о точности линеек. Металлические линейки относи­тельно точны: миллиметровые деления наносятся с погрешностью не более ±0,05 мм, а сантиметровые не более чем с точностью 0,1 мм, так что считывание результата измерения можно проводить с помощью лу­пы, снабженной дополнительной шкалой. Деревянными или пластмас­совыми линейками лучше не пользоваться: их погрешности неизвестны и могут оказаться неожиданно большими. Исправный микрометр обес­печивает точность 0,01 мм, а погрешность измерения штангенциркулем определяется точностью, с которой может быть сделан отсчет, т. е. точ­ностью нониуса. У штангенциркулей цена делений нониуса составляет обычно 0,1или 0,05 мм.

Случайные погрешности. Случайные величины, к которым отно­сятся случайные погрешности, изучаются в теории вероятностей и в математической статистике. Мы опишем — с пояснениями, но без до­казательств — основные свойства и правила обращения с такими вели­чинами в том объеме, который необходим для обработки результатов измерений, полученных в лаборатории.

Случайные погрешности устранить нельзя, но благодаря тому, что они подчиняются вероятностным закономерностям, всегда можно указать пределы, внутри которых с заданной вероятностью заключается истинное значение измеряемой величины.

Задача определения случайных погрешностей была решена созда­нием теории, хорошо согласующейся с экспериментом. В основе этой теории лежит закон нормального распределения, включающий следу­ющие закономерности:

1. При большом числе измерений ошибки одинаковой величины, но
разного знака, встречаются одинаково часто.

2. Частота появления ошибок уменьшается с ростом величины ошибки.
Иначе говоря, большие ошибки наблюдаются реже, чем малые.

3. Ошибки измерений могут принимать непрерывный ряд значений.

Случайные погрешности изучают, опираясь на изложенные законо­мерности, и для понимания такого подхода требуется ввести понятие вероятности.

Статистическая вероятность события определяется отношением числа п случаев его появления к общему числу 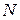всех возможных равновероятных случаев:

. (4)

 

Пусть в урне находится 100 шаров, из них 7 черных, а остальные белые. Вероятность вытащить наугад черный шар равна 7/100, веро­ятность вытащить белый — 93/100.

Применим понятие вероятности к оценке разброса случайных по­грешностей.

Проделаем п измерений какой-либо величины (например, диамет­ра стержня) и будем считать, что промахи и систематические ошиб­ки устранены и рассматривать будем только случайные ошибки. В результате этих измерений мы получим ряд значений х_п. Если х₀ есть наивероятнейшее значение измеряемой величины (пред­положим, что оно нам известно), то разность Δ х_i между измеренным значением 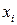и 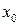называется абсолютной случайной погрешностью отдельного измерения. Тогда

…………….

 

Сложив эти равенства почленно, получим

 

, (5)

 

где 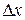могут быть как положительными, так и отрицательными чис­лами. Согласно нормальному закону распределения, погрешности, рав­ные по абсолютной величине, но противоположные по знаку, равнове­роятны. Следовательно, чем больше число измерений п, тем более веро­ятна полная взаимная компенсация погрешностей при их усреднении,

так что

.

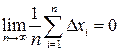Тогда

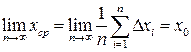. (6)

 

Следовательно, среднее арифметическое х_ср результатов отдельных из­мерений при очень большом значении п (т. е. п→∞) равно наиверо-ятнейшему значению измеряемой величины х₀. На практике п всегда конечно, и х_ср лишь приближенно равно наивероятнейшему значению измеряемой величины х₀ и тем ближе к нему, чем больше число изме­рений п.

В качестве наилучшего значения для измеряемой величины обычно принимают среднее арифметическое из всех полученных результатов:

. (7)

Чтобы оценить достоверность полученного результата, необходимо обратиться к распределению случайных погрешностей отдельных из­мерений. Распределение погрешностей часто подчиняется нормальному закону распределения (распределению Гаусса):

, (8)

где у -функция распределения (плотность вероятности) погрешно­стей:

,

 

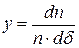где dn/(n· dδ) — доля случаев, приходящихся на бесконечно малый интервал погрешностей dδ,

х_о — наивероятнейшее значение измеряемой величины,

δ = (х — х_о) - случайная погрешность,

σ — среднеквадратичная погрешность. Величину σ ² принято назы­вать дисперсией распределения.

 

 

 

Графики закона нормального распределения с различными значе­ниями а изображены на рисунке 1.

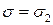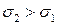Точки есть точки перегиба кривой Гаусса. Пара­метр σесть мера рассеяния случайных погрешностей δ. Если результа­ты измерений х группируются вблизи наивероятнейшего значения х₀ и значения случайных погрешностей δв основном малы, то мала и ве­личина σ(график 1, ). Наоборот, если случайные погрешности δимеют большие значения и сильно рассеяны, то кривая становится бо­лее размытой (график 2, ) и . Величина σколичественно отражает разброс значений измеряемой величины.

Отношение площади под кривой Гаусса, ограниченной значениями (на рисунке 1 эта площадь заштрихована для ), ко всей площади под кривой составляет 0,68, и запись говорит о том, что любое проведенное измерение х с вероятностью 0,68 (68%) лежит в этом интервале.

Если записано , то вероятность попадания в этот про­межуток любого проведенного измерения составляет 0,95, и если 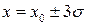, то вероятность равна 0,997.

Говоря о погрешностях, мы постоянно обращаемся к Гауссовому за­кону распределения. В пользу применения нормального закона имеют­ся серьезные основания и главное из них — центральная предельная теорема: если суммарная погрешность проявляется в результате сов­местного действия ряда факторов, каждый из которых вносит малую долю в общую погрешность, то по какому бы закону не были распре­делены погрешности, вызываемые каждым из факторов, результат их суммарного действия приведет к Гауссовому распределению погрешно­стей.

При ограниченном числе измерений п (т. е. п — конечно) отклоне­ние результата отдельного измерения от наивероятнейшего значения 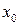оценивается выборочным среднеквадратичным отклонением :

(9)

 

Эту формулу использовать на практике невозможно, т. к. наиверо-ятнейшее значение измеряемой величины неизвестно. Однако оце­нить значение возможно, если заменить х₀ в формуле (9) сред­ним арифметическим значением х_ср:

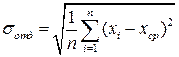(10)

Если п — невелико, то может заметно отличаться от 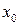и форму­ла (10) дает довольно грубую оценку . Согласно математической статистике рекомендуется использовать формулу

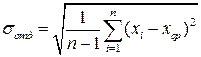(11)

 

Здесь - среднеквадратичная погрешность отдельного измерения или стандартная погрешность (стандартное отклонение), полученная путем измерений. Достоверность вычислений увеличивается с уве­личением числа измерений п.

Погрешность среднего арифметического результата измере­ния.

Практически нас больше интересует не точность каждого из п измерений, а погрешность среднего арифметического, и, главное, на­сколько оно соответствует наивероятнейшему значению измеряемой величины. Чтобы это оценить, проделаем ряд серий по п измерений величины х и найдем для каждой серии свое х_ср. Полученные средние значения х_ср колеблются по величине случайным образом около неко­торого центра 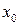, приближаясь по характеру разброса к нормально­му закону распределения. Стандартную ошибку отклонения х_ср от 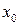можно оценить с помощью среднеквадратичной погрешности результа­та 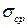(аналогично тому, как мы это делаем для для каждого из п измерений величины х). В теории вероятностей доказывается, что средняя квадратичная погрешность результата 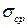связана со средней квадратичной погрешностью отдельного измерения следующим образом:

 

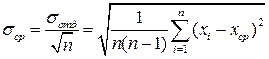. (12)

Тогда результат измерения величины х может быть представлен в виде

. (13)

Запись утверждает, что наивероятнейшее значение измеряемой ве­личины с вероятностью 0,68 (68%) лежит в интервале ( призначительном числе измерений п).

Погрешность 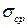обычно называют стандартной погрешностью опы­та, а ее квадрат — дисперсией.

Можно показать, что, как правило, погрешностьрезультата измере­ний только в 5% случаях превосходит и почти всегда оказывается меньше .

На первый взгляд, из сказанного можно сделать вывод, что, беспре­дельно увеличивая число измерений, можно даже с самой примитив­ной аппаратурой получить очень хорошие результаты. Это, конечно, не так. С увеличением числа измерений уменьшается случайная погреш­ность опытов. Систематические погрешности, связанные с несовершен­ством приборов, при увеличении числа опытов не меняются, т. е. число опытов следует выбирать разумно, не завышая его неоправданно.

Если число опытов мало (менее 8), лучше применять другие, более сложные оценки. Следует иметь в виду, что при п ≈ 10 измерение 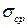определяется с точностью до 20-30%. Поэтому расчет погрешностей следует выполнять с точностью до двух знаков, не более.

 

Сложение случайных и систематических погрешностей. В ре­альных опытах присутствуют как систематические, так и случайные ошибки. Пусть они характеризуются погрешностям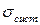и и 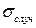. Сум­марная погрешность находится по формуле

. (14)

которая показывает, что при наличии как случайной, так и системати­ческой погрешности полная ошибка опыта больше, чем каждая из них в отдельности.

Обратим внимание на важную особенность формулы. Пусть одна из ошибок, например, 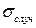в 2 раза меньше другой - в нашем случае .

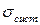Тогда

.

В нашем примере с точностью 12% . Таким образом, меньшая погрешность почти ничего не добавляет к большей, даже ес­ли она составляет половину от нее. Данный вывод очень важен. В том случае, когда случайная ошибка опытов хотя бы вдвое меньше система­тической, нет смысла производить многократные измерения, так как полная погрешность опыта при этом практически не уменьшается. Из­мерения достаточно произвести 2-3 раза, чтобы убедиться, что случай­ная ошибка действительно мала.

Обработка результатов при косвенных измерениях. Если иссле­дуемая величина представляет собой сумму или разность двух изме­ренных величин

, ( 15)

 

то наилучшее значение величины а равно сумме (или разности) наилуч­ших значений слагаемых: , или, как рекомендовано выше,

 

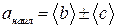. (16)

 

Здесь и в дальнейшем угловые скобки (или черта сверху) означают усреднение: вместо того, чтобы писать а _ср, будем пользоваться обозна­чением (а) (или ) и т. д.

Среднеквадратичная погрешность 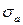, если величины а и b незави­симы, находится по формуле

, (17)

т. е. погрешности, как всегда, складываются квадратично, или, что то же самое, складываются дисперсии результатов измерений.

В том случае, если искомая величина равна произведению или част­ному двух других

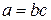или , (18)

то

или . (19)

 

Относительная среднеквадратичная погрешность произведения или частного независимых величин находится по формуле

 

. (20)

 

Приведем расчетные формулы для случая, когда

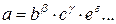(21)

Наилучшее значение а связано с наилучшими значениями Ь, с и е и т. д. той же формулой (21), что и каждое конкретное значение. Относительная среднеквадратичная погрешность величины а при неза­висимых b, с, е,... определяется формулой

(22)

Наконец, приведем для справок общую расчетную формулу. Пусть

(23)

где f - произвольная функция величин b, с, е и т. д. Тогда

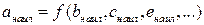. (24)

Формула (24) справедлива как в случае, когда b_наил, с_наил и т. д. непо­средственно измерены, так и в случае, если они сами найдены по изме­ренным значениям других величин. В первом случае значения b_наил, с_наил и т. д., как уже указывалось, равны 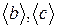и т. д.

Погрешность а находится по формуле

(25)

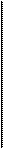Обозначение df / db имеет обычный смысл частной производной функ­ции f по b, т. е. производной, при вычислении которой все остальные аргументы, кроме b (в нашем случае с, е и т. д.), считаются постоян­ными. Аналогичный смысл имеют частные производные по с, е и т. д. Частные производные следует вычислять при наилучших значениях аргументов b_наил, с_наил, е_наил и т. д. Формулы (17), (20) и (22) являются частными случаями формулы (25).

Рассмотрим некоторые следствия, которые могут быть получены из анализа формул, приведенных в этом разделе. Прежде всего заме­тим, что следует избегать измерений, при которых искомая величина находится как разность двух больших чисел. Так, толщину стенки тру­бы лучше измерять непосредственно, а не определять, вычитая внут­ренний диаметр из внешнего (и, конечно, деля результат пополам). Относительная погрешность измерения, которая обычно представляет главный интерес, при этом сильно увеличивается, так как измеряемая величина — в нашем случае толщина стенки — мала, а ошибка в ее определении находится путем сложения погрешностей измерения обо­их диаметров и поэтому возрастает. Следует также помнить, что по­грешность измерения, которая составляет, например, 0,5% от величины внешнего диаметра, может составить 5 и более процентов от толщины стенки.

При измерениях, которые затем обрабатываются по формуле (18) (например, при определении плотности тела по его массе и объему), следует определять все измеряемые величины с приблизительно оди­наковой относительной точностью. Так, если объем тела измерен с по­грешностью 1%, то при взвешивании с погрешностью 0,5% его плот­ность определяется с точностью 1,1%, а при взвешивании с погрешностью 0,01% — с точностью 1%, т. е. с той же практически точностью. Тратить силы и время на измерение массы тела с точностью 0,01% в этом случае, очевидно, не имеет смысла. При измерениях, которые обрабатываются по формуле (21), сле­дует обращать главное внимание на точность измерения величины, вхо­дящей в расчетную формулу с наибольшим показателем степени.

Прежде чем приступить к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рас­считываться погрешности. Эти формулы позволят понять, какие изме­рения следует производить особенно тщательно, а на какие не нужно тратить больших усилий.