Расчеты выполнены в программе MathCAD.
Передаточная функция в операторной форме имеет вид:
. (2.1)
Передаточная функция в комплексно частотной форме имеет вид:
 |
(2.2)
С помощью нижеприведенных команд определим вещественную и мнимую составляющие.
Нерасширенная АФХ объекта приведена на рисунке 2.1.
Рисунок 2.1 – Нерасширенная АФХ объекта
2.2 Расширенная АФХ объекта для показателя колебательности m = 0.4
Для получения расширенной АФХ объекта произведем замену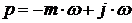 
, тогда передаточная функция для показателя колебательности
m = 0.4 будет иметь вид:
(2.3)
Расширенная АФХ объекта для показателя колебательности m = 0.4 приведена на рисунке 2.2.
Рисунок 2.2 – Расширенная АФХ объекта для показателя колебательности m = 0.4
Определим по формулам 1.1 и 1.2 параметры настройки регулятора и построим зависимость коэффициента интегральной составляющей от коэффициента пропорциональной составляющей.
Рисунок 2.3 – График зависимости 
от 
для показателя колебательности m = 0.4
Наилучшими динамическими свойствами обладает система с максимальными коэффициентами. Из графика определяем Kp=0.013, Ku=2.896*10-4. Так как постоянная времени интегрирования равна Ti=Kp/Ku=46.505, то передаточная функция регулятора имеет вид:
(2.4)
Переходной процесс разомкнутой системы приведен на рисунке 2.4.
Рисунок 2.4 – Переходной процесс разомкнутой системы
Переходной процесс замкнутой системы с учетом регулятора приведен на рисунке 2.5.
Рисунок 2.5 – Переходной процесс замкнутой системы с учетом регулятора для показателя колебательности m = 0.4
Перерегулирование 
%. Время регулирования tр=
2.3 Расширенная АФХ объекта для показателя колебательности m = 0.7
Для получения расширенной АФХ объекта произведем замену 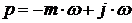, тогда передаточная функция для показателя колебательности
m = 0.7 будет иметь вид:
(2.5)
Расширенная АФХ объекта для показателя колебательности m = 0.7 приведена на рисунке 2.6.
Рисунок 2.6 – Расширенная АФХ объекта для показателя колебательности
m = 0.7
Определим по формулам 1.1 и 1.2 параметры настройки регулятора и построим зависимость коэффициента интегральной составляющей от коэффициента пропорциональной составляющей.
Рисунок 2.7 – График зависимости от для показателя колебательности
m = 0.7
Наилучшими динамическими свойствами обладает система с максимальными коэффициентами. Из графика определяем Kp=8.614*10-3, Ku=1.769*10-4. Так как постоянная времени интегрирования равна Ti=Kp/Ku=48.689, то передаточная функция регулятора имеет вид:
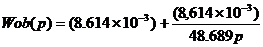(2.6)
Переходной процесс замкнутой системы с учетом регулятора приведен
на рисунке 2.8.
Рисунок 2.8 – Переходной процесс замкнутой системы с учетом регулятора для показателя колебательности m = 0.7
Перерегулирование 
%.
Время регулирования tр=
ВЫВОДЫ
В результате выполнения данной лабораторной работы изучен синтез регуляторов методом расширенных частотных характеристик.
Построена нерасширенная АФХ объекта, приведенная на рисунке 2.1. Построена расширенная АФХ объекта для показателя колебательности m = 0.4, приведенная на рисунке 2.3, рассчитаны настройки регулятора и определена передаточная функция (2.4) ПИ-регулятора. Построен переходной процесс разомкнутой системы (рисунок 2.4) и переходной процесс замкнутой системы (рисунок 2.5) с учетом регулятора для показателя колебательности m = 0.4.
Построена расширенная АФХ объекта для показателя колебательности
m = 0.7, приведенная на рисунке 2.6, рассчитаны настройки регулятора и определена передаточная функция (2.6) ПИ-регулятора. Построен переходной процесс замкнутой системы (рисунок 2.8) с учетом регулятора для показателя колебательности m = 0.7.
Анализируя переходные процессы замкнутой системы с учетом регулятора можно сделать вывод, что чем больше выбран показатель колебательности при расчете настроек регулятора, тем устойчивее работа системы.