ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
Электрический ток. Сила и плотность тока
Электрическим током называется всякое упорядоченное движение электрических зарядов. Электрический ток, возникающий в проводящих средах в результате упорядоченного движения свободных зарядов под действием электрического поля, созданного в этих средах, называется током проводимости. Примерами токов проводимости являются ток в металлах, связанный с упорядоченным движением «свободных» электронов, ток в электролитах, представляющий собой упорядоченное перемещение ионов противоположных знаков.
За направление тока принимают движение положительных электрических зарядов. Однако в действительности в металлических проводниках ток осуществляется упорядоченным движением электронов, которые движутся в направлении, противоположном направлению тока.
Силой тока I называется скалярная физическая величина, равная отношению заряда d q, переносимого сквозь рассматриваемую поверхность (в случае тока проводимости – через поперечное сечение проводника) за малый промежуток времени, к величине d t этого промежутка
(2.1)
Электрический ток называется постоянным, если сила тока и его направление не изменяются с течением времени. Для постоянного тока
(2.2)
где q – электрический заряд, переносимый через рассматриваемую поверхность за конечный промежуток времени от 0 до t.
Вектор плотности тока 
численно равен отношению силы тока d I через малый элемент поверхности, нормальный к направлению движения заряженных частиц, к величине 
площади этого элемента
(2.3)
Вектор совпадает по направлению с движением положительно заряженных носителей тока. Зная плотность тока, силу тока через произвольную поверхность S определяют как
(2.4)
где 
– проекция вектора j на направление нормали 
к элементу поверхности, а интегрирование проводится по всей площади поверхности S.
Плотность постоянного тока одинакова по всему поперечному сечению S однородного проводника. Для такого тока
(2.5)
Основы классической электронной теории
электропроводности металлов
Высокая электропроводность металлов связана с тем, что в металлах имеется большое количество носителей тока – электронов проводимости, образовавшихся из валентных электронов атомов металла, которые не принадлежат определенному атому, а являются коллективизированными (обобществленными) электронами. В классической электронной теории Друде–Лоренца эти электроны рассматриваются как электронный газ, обладающий свойствами одноатомного идеального газа.
Концентрация электронов проводимости в одновалентном металле равна концентрации его атомов: 
, где 
– постоянная Авогадро, А – атомная масса металла, r – его плотность. По порядку величины n0 ~ (1028–1029) м–3.
В отсутствие электрического поля внутри металла электроны проводимости движутся хаотически и сталкиваются с ионами кристаллической решетки металла.
Средняя кинетическая энергия теплового хаотического движения электронов
где т – масса электрона, 
– средняя квадратичная скорость электронов. При температуре Т = 273 К скорость = 105 м/с.
Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение (дрейф) электронов. Плотность тока равна заряду всех электронов, проходящих за единицу времени через единицу площади поперечного сечения проводника:
(2.6)
где 
– концентрация электронов проводимости, е – абсолютная величина заряда электрона, á v ñ – средняя скорость дрейфа электронов под действием внешнего электрического поля. При самых больших плотностях тока 
м/с, т. е. скорость дрейфа электронов ничтожно мала по сравнению со средней скоростью их теплового движения.
Закон Ома для плотности тока (закон Ома в дифференциальной форме): плотность тока проводимости пропорциональна напряженности 
электрического поля в проводнике и совпадает с ней по направлению, т. е.
(2.7)
Коэффициент пропорциональности g называется удельной электрической проводимостью среды (удельной электропроводностью), а величина r = 1/g называется удельным электрическим сопротивлением среды.
Этот закон выводится в классической электронной теории электропроводности металлов при следующих двух предположениях:
а) концентрация электронов проводимости не зависит от напряженности электрического поля в проводнике;
б) средняя скорость упорядоченного движения электронов проводимости, приобретаемая ими на длине свободного пробега под действием электрического поля, во много раз меньше средней скорости á u ñ их теплового движения, т. е. еЕ álñ<< k T, где е – абсолютная величина заряда электрона, álñ – средняя длина свободного пробега электронов проводимости, k – постоянная Больцмана, Т – температура.
Согласно классической электронной теории
(2.8)
и
(2.9)
где т – масса электрона.
Проходя расстояние равное длине свободного пробега электрон приобретает под действием поля скорость упорядоченного движения, равную 
. При соударении с ионом электрон теряет скорость, и энергия упорядоченного движения электрона преобразуется во внутреннюю энергию проводника, который нагревается при прохождении по нему электрического тока.
Объемной плотностью тепловой мощности тока называется величина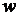 
, численно равная энергии, которая выделяется в единице объема проводника за единицу времени.
Закон Джоуля–Ленца в дифференциальной форме: объемнаяплотность тепловой мощности тока равна скалярному произведению векторов плотности тока и напряженности электрического поля:
(2.10)
Закон Видемана – Франца: для всех металлов отношение коэффициента теплопроводности К к удельной электрической проводимости g прямо пропорционально термодинамической температуре Т:
(2.11)
где k – постоянная Больцмана, е – элементарный заряд.
Недостатки классической электронной теории электропроводности металлов:
а) невозможность объяснить экспериментально наблюдаемую в широком интервале температур линейную зависимость между удельным сопротивлением r и термодинамической температурой r ~ Т;
б) неправильное значение молярной теплоемкости металлов. Она должна быть равна, согласно этой теории, 9 R /2 (R – универсальная газовая постоянная) и складываться из теплоемкости ионной кристаллической решетки (3 R) и теплоемкости одноатомного электронного газа (3 R /2). Однако из опытного закона Дюлонга и Пти известно, что молярная теплоемкость металлов мало отличается от теплоемкости кристаллических диэлектриков и приблизительно равна 3 R. Объяснить это расхождение теории с экспериментом классическая физика не может;
в) экспериментальные значения удельного сопротивления r и теоретические значения средней арифметической скорости электронов приводят по формуле (2.9) к величине средней длины свободного пробега электрона álñ, на два порядка превышающей период кристаллической решетки металла. Это противоречит предположениям классической электронной теории электропроводности металлов.