Определение.
Пусть даны две переменные х и y с областями изменения Х и Y. Переменная y называется функцией от х, если по некоторому правилу или закону каждому значению 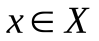 ставится в соответствие одно определенное значение
ставится в соответствие одно определенное значение  .
.
Задать функцию – это значит указать правило, позволяющее по данному значению независимой переменной находить соответствующее значение функции.
Существует три основных способа задания функции: аналитический, табличный и графический.
1 .Аналитический способ состоит в том, что зависимость между переменными величинами задается в виде формулы (аналитического выражения), указывающей, какие и в каком порядке действия надо выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.
1. Аналитический способ является наиболее совершенным, т.к. к нему могут быть применены методы математического анализа, позволяющие полностью исследовать функцию.
2. Табличный способ предусматривает задание таблицы, в которой различным значениям аргумента  поставлены соответствующие значения функции
поставлены соответствующие значения функции 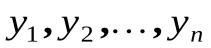 :
:
3. Графический способ задания функции состоит в том, что в данной системе координат задается некоторая кривая. Преимуществом графического задания является его наглядность, недостатком – его неточность.
Вопрос 2
Окрестность точки, множества и её свойства, предел функции
Определение 1. Окрестностью точки 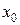 радиуса
радиуса 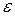 (
(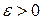 ) называется множество всех действительных чисел
) называется множество всех действительных чисел 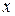 таких, что
таких, что  (рис. 11а).
(рис. 11а).
Определение 2. Проколотой окрестностью точки 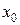 радиуса
радиуса 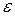 (
(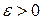 ) называется множество всех действительных чисел
) называется множество всех действительных чисел 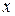 таких, что
таких, что  (рис. 11б).
(рис. 11б).
Обозначения: 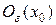 –
– 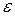 -окрестность точки
-окрестность точки 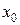 ;
;
 – проколотая
– проколотая 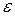 -окрестность точки
-окрестность точки 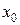 .
.

|
Предел функции – величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к заданной точке.
Вопрос 3
Замечательные пределы, их следствия
Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения двух широко известных математических тождеств со взятием предела:
| Первый замечательный предел{\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1.} | следствия первого замечательного предела{\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1.} | Второй замечательный предел {\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1.} | следствия второго замечательного предела |
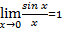
|  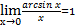
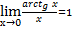
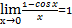
| 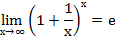
| 
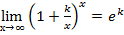 

 для а>0, а≠1 для а>0, а≠1
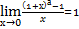
|
Вопрос 4
Бесконечно малые функции, их свойства, сравнение
Бесконечно малая функция — числовая функция или последовательность, которая стремится к нулю.
Функция y=f(x)называется бесконечно малой (илибесконечно малой величиной) при 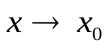 , если
, если  . Например,
. Например, 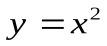 б.м. при х→0, т.к.f(x) →0, т.е.
б.м. при х→0, т.к.f(x) →0, т.е. 
Свойства бесконечно малых [Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
· Произведение бесконечно малых — бесконечно малая.
· Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
· Если {\displaystyle a_{n}}бесконечно малая последовательность, сохраняющая знак, то {\displaystyle b_{n}={\dfrac {1}{a_{n}}}} бесконечно большая последовательность
Сравнение
Если 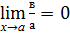 то {\displaystyle \beta } — бесконечно малая высшего порядка малости, чем {\displaystyle \alpha }. Обозначают {\displaystyle \beta =o(\alpha)} или {\displaystyle \beta \prec \alpha } в>a.
то {\displaystyle \beta } — бесконечно малая высшего порядка малости, чем {\displaystyle \alpha }. Обозначают {\displaystyle \beta =o(\alpha)} или {\displaystyle \beta \prec \alpha } в>a.
Если  то {\displaystyle \beta } — бесконечно малая низшего порядка малости, чем {\displaystyle \alpha }. Соответственно {\displaystyle \alpha =o(\beta)} или a>в{\displaystyle \alpha \prec \beta }.
то {\displaystyle \beta } — бесконечно малая низшего порядка малости, чем {\displaystyle \alpha }. Соответственно {\displaystyle \alpha =o(\beta)} или a>в{\displaystyle \alpha \prec \beta }.
Если  (предел конечен и не равен 0), то {\displaystyle \alpha } и {\displaystyle \beta } являются бесконечно малыми величинами одного порядка малости. Это обозначается как {\displaystyle \alpha \asymp \beta }а~в или как одновременное выполнение отношений {\displaystyle \beta =O(\alpha)} в=0(а) и {\displaystyle \alpha =O(\beta)}а=0(в).
(предел конечен и не равен 0), то {\displaystyle \alpha } и {\displaystyle \beta } являются бесконечно малыми величинами одного порядка малости. Это обозначается как {\displaystyle \alpha \asymp \beta }а~в или как одновременное выполнение отношений {\displaystyle \beta =O(\alpha)} в=0(а) и {\displaystyle \alpha =O(\beta)}а=0(в).
Если  предел конечен и не равен 0), то бесконечно малая величина {\displaystyle \beta }в имеет {\displaystyle m}m -й порядок малости относительно бесконечно малой {\displaystyle \alpha }.
предел конечен и не равен 0), то бесконечно малая величина {\displaystyle \beta }в имеет {\displaystyle m}m -й порядок малости относительно бесконечно малой {\displaystyle \alpha }.
Вопрос 10
Таблица производных элементарных функций

Вопрос 11
Производная высшего порядка, механический смысл второй производной
Под производной высших порядков понимают дифференцирования функции более одного раза. Если производную 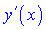 повторно дифференцировать, то получим производную второго порядка, или вторую производную функции
повторно дифференцировать, то получим производную второго порядка, или вторую производную функции 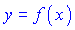 , и она обозначается
, и она обозначается
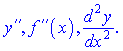
Производная третьего порядка будет иметь вид

Аналогично получают формулы для нахождения производных высших порядков. При нахождении производной 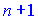 порядке необходимо иметь производную
порядке необходимо иметь производную 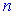 порядка. Исключение составляют функции для которых можно заметить тенденцию изменения производных. Это степенные, некоторые тригонометрические и экспоненциальные функции:
порядка. Исключение составляют функции для которых можно заметить тенденцию изменения производных. Это степенные, некоторые тригонометрические и экспоненциальные функции:

В других случаях, для нахождения производных высших порядков от заданной функции нужно последовательно находить все ее производные низших порядков. Для практического усвоения материала рассмотрим примеры.
Механический смысл второй производной.
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть 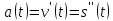
Вопрос 8
Геометрический и физический смыслы производной

1) Физический смысл производной.
Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная 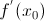 – скорость изменения переменной y относительно переменной x в точке
– скорость изменения переменной y относительно переменной x в точке 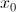 . Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная
. Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная 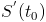 – скорость в момент времени
– скорость в момент времени  . Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то
. Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то 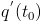 – скорость изменения количества электричества в момент времени
– скорость изменения количества электричества в момент времени  , т.е. сила тока в момент времени
, т.е. сила тока в момент времени  .
.
Вопрос 9
Теоремы о производных суммы, произведения и частного. Производная сложной и обратной функции.
Теорема. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: (u±ν)'=u'±ν'.
Теорема справедлива для любого конечного числа слагаемых.
Теорема. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: (u•ν)'=u'ν+v'u.
т. е. (u•ν)'=u'•ν+u•ν'.
При доказательстве теоремы использовалась теорема о связи непрерывности и дифференцируемости: так как функции u=u(х) и ν=ν(х) дифференцируемы, то они и непрерывны, поэтому ∆ν→0 и ∆u→0 при ∆х→0.
Можно показать, что:
а) (с•u)'=с•u', где с = const;
б) (u•ν•w)'=u'v•w+u•v'•w+u•v•w'.
Теорема. Производная частного двух функций  , если v (x) ≠0 равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя
, если v (x) ≠0 равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя 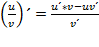 , v ≠ 0.
, v ≠ 0.
Следствие. 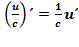 . Следствие.
. Следствие. 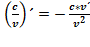 ,где с = const.
,где с = const.
Пусть у = f (и) и и = φ (x), тогда у=f (φ (x)) — сложная функция с промежуточным аргументом и и независимым аргументом х.
Теорема. Если функция и = φ (х)имеет производную  в точке х, а функция у = f (u)имеет производную
в точке х, а функция у = f (u)имеет производную 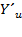 соответствующей точке и = φ(х), то сложная функция у = f (φ(x))имеет производную
соответствующей точке и = φ(х), то сложная функция у = f (φ(x))имеет производную  вточке х, которая находится по формуле:
вточке х, которая находится по формуле: 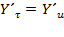 *
*  .
.