ОГЛАВЛЕНИЕ
ЗАДАЧА 1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПРИВОДА.. 2
1.1 Построение плана положения механизма. 2
1.2Структурный анализ механизма. 2
1.3Построение плана скоростей. 3
1.4 План ускорений. 5
ЗАДАЧА № 2. РАСЧЕТ ТОРМОЗНОГО УСТРОЙСТВА.. 8
ЗАДАЧА 3. РАСЧЕТ СВАРНЫХ СОЕДИНЕНИЙ.. 12
ЗАДАЧА 1.КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПРИВОДА
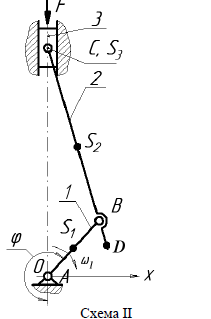
ω1=24 об /мин. – частота вращения тихоходного вала редуктора
φ=240, град. lAB = 0,10м, lBC =0,25м, lCD =0,40м
1.1Построение плана положения механизма
Масштаб:
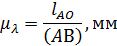
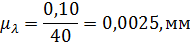
Длина кривошипа: АВ=40мм.
Длины звеньев механизма в масштабе построения:
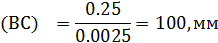
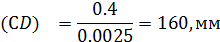
Структурный анализ механизма
Механизм содержит три подвижных звена и одно неподвижное звено 0 (стойка). Подвижные звенья и стойка образуют 4 кинематические пары V класса, из которых три – вращательные и одна – поступательная (табл. 1.1).
Таблица 1.1
Наименование, класс и обозначение кинематических пар, образующих механизм
| № п/п | Обозначение кинематической пары | Звенья, образующие кинематическую пару | Класс кинематической пары | Наименование кинематической пары |
| А | 0 и 1 | V | вращ. | |
| В | 1 и 2 | V | вращ. | |
| С | 2 и 3 | V | вращ. | |
| D | 3 и 0 | V | поступ. |
Формула строения механизма:
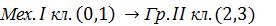 =
= 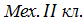
Степень свободы механизма по структурной формуле Чебышева:
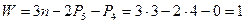
Где n=3 – подвижные звенья механизма
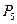 =4- пары низшего порядка,
=4- пары низшего порядка,
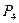 =0 - пары высшего порядка.
=0 - пары высшего порядка.
1.3Построение плана скоростей
1. Кинематический анализ механизма в положении, заданном положением углом φ1 =240º.
| № п/п | Определяе-мая величина | Расчетная формула | Резуль-тат расчета | Методические указания | ||
| 1. Определение линейных и угловых скоростей | ||||||
| 1.1 | Скорость точки В VВ | 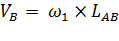
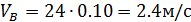
| 2.4 м/с | Рассмотрим группу Ассура 2-3 и определим линейные скорости точек этой группы. Первой такой точкой является точка В, которая относительно точки А совершает вращательное движение. Вектор скорости точки В направлен в сторону вращения ω1 перпендикулярно звену АВ (см. чертеж, план скоростей) | ||
| 1.2 | Масштаб плана скоростей | 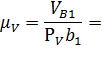
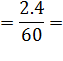
| 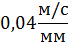
| Из произвольно выбранной точки Р(полюс плана скоростей: начало отсчета) отложить перпендикулярно звену АВ отрезок (Рb)=60 мм, который на схеме изображает величину век-тора скорости т. В (VВ= 2.4 м/с) | ||
| 1.3 | Скорость точки С
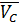
| 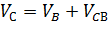
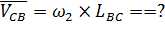
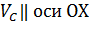
| Следующая точка - точкаС.
На основании теоремы о сложении скоростей в сло-жном движении точки С ее скорость 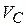 будет опре-деляться векторами скорости точки В ( будет опре-деляться векторами скорости точки В (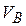 ) и скорости ) и скорости 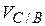 (относи-тельного вращательного
движения точки С вокруг точки В). Величина скорос-ти (относи-тельного вращательного
движения точки С вокруг точки В). Величина скорос-ти 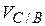 неизвестна, т.к. не задано значение угловой скорости звена 2 неизвестна, т.к. не задано значение угловой скорости звена 2 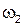 ; при этом ; при этом Точка С движется возврат-но-поступательно вдоль оси ОХ, поэтому полный вектор направляющей). Их пересе-чение определяет
| |||
Из плана
скоростей:
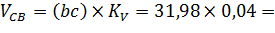
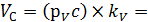
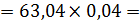
| 1.3м/с 2,52м/с | положение точки «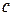 ». Направление векторов
скоростей осуществляется в соответствии с векторным уравнением для точки С.
Значение скоростей VCB и VC (в м/с) определяется из плана скоростей измерением отрезков (bc) и VC (в м/с) и умножением этих значений на величину масштаба скорости kV ». Направление векторов
скоростей осуществляется в соответствии с векторным уравнением для точки С.
Значение скоростей VCB и VC (в м/с) определяется из плана скоростей измерением отрезков (bc) и VC (в м/с) и умножением этих значений на величину масштаба скорости kV
| ||||
| 1.4 | Угловая скорость звена 2
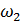
| 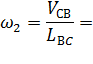
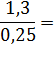
|
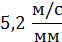
| Для определения направления угловой скорости 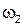 необходимо условно перенести в точку С механизма вектор скорости необходимо условно перенести в точку С механизма вектор скорости 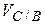 , а точку В условно закрепить. Тогда вектор , а точку В условно закрепить. Тогда вектор 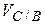 будет вращать точку С относительно В по часовой стрелке. будет вращать точку С относительно В по часовой стрелке.
| ||
| 1.5 | Скорость
точки D
механизма 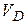
| 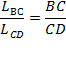 где
где 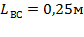 - размер участка звена 2; - размер участка звена 2;
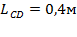 - размер звена 2;
ВС= 31,98мм – размер на плане скоростей;
СD - - размер звена 2;
ВС= 31,98мм – размер на плане скоростей;
СD -  размер на плане скоростей.
Тогда размер на плане скоростей.
Тогда
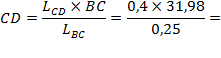
|
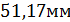
| |||
.
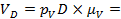
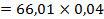 = =
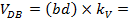
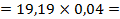
|
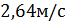 0.76м/с
0.76м/с
| Скорость точки D Скорость точки D при ее вращении вокруг точки В | ||||
| 1.6 | Скорости
точек центров
тяжести
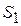 , , 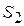 и и 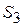 звеньев
( звеньев
(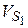 , , 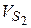 и и 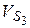 ). ).
| 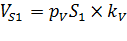 = = 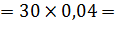
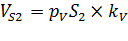 = = 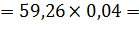
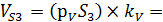
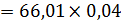
| 1.2 м/с 2.37м/с 2,64м/с | Точки центров тяжести 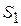 и и 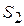 звеньев расположены посередине длин соответствующих звеньев, а центр тяжести звеньев расположены посередине длин соответствующих звеньев, а центр тяжести 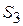 расположен в шарнире С (см. задание). Поэтому точки « расположен в шарнире С (см. задание). Поэтому точки «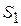 » и « » и «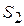 » будут расположены на плане скоростей посередине
отрезков » будут расположены на плане скоростей посередине
отрезков 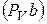 и и 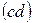 , а скорость точки , а скорость точки 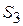 будет равна скорости точки С. Значения скоростей точек будет равна скорости точки С. Значения скоростей точек
 (в м/с) определяют из плана скоростей измерением соответствующих отрезков и умножением этих
значений на величину масштаба скорости (в м/с) определяют из плана скоростей измерением соответствующих отрезков и умножением этих
значений на величину масштаба скорости 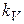
|
План ускорений
| № п/п | Определяе-мая величина | Расчетная формула | Резуль-тат расчета | Методические указания | ||
| 2.1 | Ускорение точки В
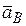
| 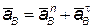
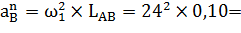 (направлено вдоль звена АВ от точки В
к точке А)
(направлено вдоль звена АВ от точки В
к точке А)
| 57,6м/с2 | Рассмотрим группу Ассура 2-3 и определим линейные ускорения точек этой группы. Первой точкой является точка В. В общем виде ускорение любой точки можно представить как векторную | ||
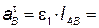
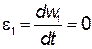 (т.к.
(т.к. 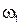 = const) = const)
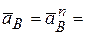
|
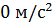 57,6 м/с2
57,6 м/с2
|
векторную сумму нормального 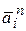 и танген-циального и танген-циального 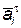 ускорений
Абсолютная величина нор-мального ускорения равна ускорений
Абсолютная величина нор-мального ускорения равна 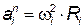 , где , где 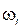 - угловая скорость звена (рад/с), - угловая скорость звена (рад/с), 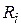 - радиус вращения звена, м. Вектор нормального ускорения на-правлен вдоль радиуса от точки к центру ее вращения. - радиус вращения звена, м. Вектор нормального ускорения на-правлен вдоль радиуса от точки к центру ее вращения.
| ||||
| 2.2 | Масштаб плана ускорений
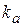
| 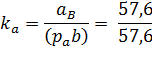
|
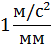
| Из произвольной точки 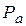 (полюс плана ускорений - начало отсчета) отложить параллельно звену АВ отрезок (полюс плана ускорений - начало отсчета) отложить параллельно звену АВ отрезок 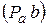 = 57,6мм, который в масштабе = 57,6мм, который в масштабе 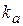 изображает величину век-тора ускорений точки В
(см. чертеж, план ускоре-ний) изображает величину век-тора ускорений точки В
(см. чертеж, план ускоре-ний)
| ||
| 2.3 | Ускорение точки С
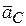
|
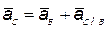
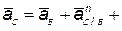
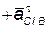
| Общее ускорение точки С складывается из ускорения точки В и ускорения точки С
при ее вращении вокруг точки В.
Ускорение точки С при ее вращении вокруг точки В (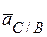 ) может быть разложено на нормальное ) может быть разложено на нормальное 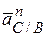 и тангенциальное и тангенциальное 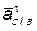
| |||
Нормальное
ускорение
точки С при
ее вращении
вокруг точки В
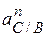 Тангенциальное
ускорение
точки С при
ее вращении
вокруг точки В
Тангенциальное
ускорение
точки С при
ее вращении
вокруг точки В

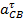
| 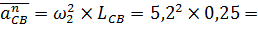 (направлено // ВС от точки С к точке В)
(направлено // ВС от точки С к точке В)
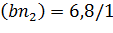
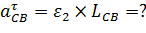
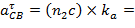 =50,66∙1=
=50,66∙1=
| 6,8м/с2 6,8 мм 50,66м/с2 | Полученные уравнения решаем графоаналитическим методом.
Отрезок 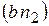 = 6,8 мм, представляющий в масштабе = 6,8 мм, представляющий в масштабе 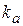 вектор ускорения вектор ускорения 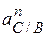 , отложить от точки « , отложить от точки «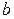 » плана ускорений в направ-лении от точки С к точке В механизма (см. чертеж, план ускорений).
Величина ускорения » плана ускорений в направ-лении от точки С к точке В механизма (см. чертеж, план ускорений).
Величина ускорения 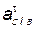 остается неизвестной, т.к. остается неизвестной, т.к. 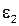 =? Известно лишь, что =? Известно лишь, что 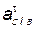 ^ ВС.
Поскольку нормальное и тангенциальное ускорения
взаимно перпендикулярны, то через точку ^ ВС.
Поскольку нормальное и тангенциальное ускорения
взаимно перпендикулярны, то через точку 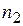 плана ускорений проводим прямую, перпендикулярную отрезку плана ускорений проводим прямую, перпендикулярную отрезку 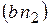 до пересе-чения с горизонтальной прямой - линией действия ускорения точки С, прове-денной из полюса Р. Точку пересечения обозначаем до пересе-чения с горизонтальной прямой - линией действия ускорения точки С, прове-денной из полюса Р. Точку пересечения обозначаем 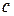 .
Значения ускорений (м/с 2 ) определяют из плана уско-рений измерением соот-ветствующих отрезков и умножением этих значений на величину масштаба плана ускорений .
Значения ускорений (м/с 2 ) определяют из плана уско-рений измерением соот-ветствующих отрезков и умножением этих значений на величину масштаба плана ускорений 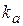 . .
| |||
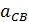
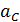
| 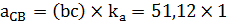
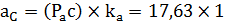
| 51,12 м/с2 17,63м/с2 | ||||
| 2.4 | Угловое
ускорение
звена 2
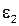
| 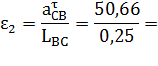
|
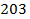
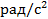
| Для определения на-правления вектора углового ускорения 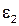 необходимо условно перенести вектор тан-генциального уско-рения необходимо условно перенести вектор тан-генциального уско-рения 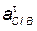 в точку С механизма, а точку В - условно закрепить. Тогда искомый вектор будет вращать точку С
относительно точки В против часовой стрелки в точку С механизма, а точку В - условно закрепить. Тогда искомый вектор будет вращать точку С
относительно точки В против часовой стрелки
| ||
| 2.5 | Ускорения центров
тяжести
звеньев (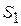 , , 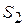 и и 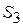 ) и точки D ) и точки D
| 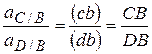 Отсюда: Отсюда:
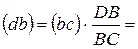
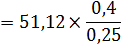
| 81,8мм | Положение центров тяжести звеньев
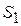 , , 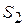 и и 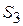 , а также точки D
определяется на осно-вании свойств планов скоростей и ускорений (см. пункт 1.5 данной таблицы).
От точки « , а также точки D
определяется на осно-вании свойств планов скоростей и ускорений (см. пункт 1.5 данной таблицы).
От точки «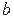 » на пря-мой » на пря-мой 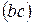 отложить отрезок отложить отрезок 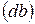 Соединить полученную точку « Соединить полученную точку «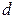 » » 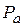 . .
| ||
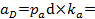
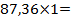
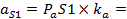
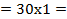
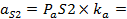
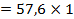
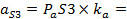
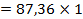
| 87,36м/с2 30м/с2 57,6 м/с2 87,36 м/с2 | План ускорений построен
в масштабе 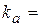 1 1 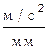 Значения ускорений точек
Значения ускорений точек 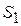 , , 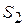 , , 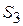 и D
(в м/с 2 ) определяют из плана ускорений
измерением соответст-вующих отрезков и умножением этих значений на
величину масштаба ускорений и D
(в м/с 2 ) определяют из плана ускорений
измерением соответст-вующих отрезков и умножением этих значений на
величину масштаба ускорений  .
Вектор .
Вектор 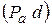 изображает в масштабе ускорение точки D механизма ( изображает в масштабе ускорение точки D механизма (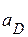 )
Вектор )
Вектор 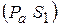 изображает в масштабе ускорение точки изображает в масштабе ускорение точки 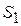 механизма ( механизма (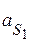 )
Вектор )
Вектор  изображает в масштабе ускорение точки изображает в масштабе ускорение точки 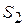 механизма ( механизма (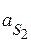 )
Ускорение точки )
Ускорение точки 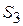 равно ускорению точки С, т.к. центр тяжести равно ускорению точки С, т.к. центр тяжести 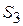 расположен в шарнире С расположен в шарнире С
|
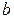 » плана скоростей провести прямую перпендикулярно звену ВС, а из полюса
» плана скоростей провести прямую перпендикулярно звену ВС, а из полюса 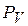 - прямую, параллельно оси ОХ (т.е. параллельно
- прямую, параллельно оси ОХ (т.е. параллельно