Наибольшее и наименьшее значения функции.

Лекция (к занятию № 28)

Наибольшим значением функции называется самое большое, а наименьшим значением - самое меньшее из всех её значений.

Функция может иметь только одно наибольшее значение и только одно наименьшее значение или может не иметь их совсем.

Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:

1. Если в некотором открытом промежутке 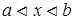(конечном или бесконечном) функция 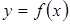непрерывна и имеет только один экстремум и если это максимум, то он и является наибольшим значением функции, а если минимум – наименьшим значением функции в этом промежутке;

2. Если функция 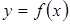непрерывна на отрезке: 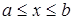, то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри отрезка, или на концах этого отрезка. Поэтому, чтобы найти наибольшее и наименьшее значения функции на отрезке 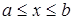, где она непрерывна следует:

- Найти экстремумы функции на данном отрезке;

- Найти значения функции на концах отрезка: 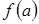и ;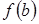

- Из всех найденных значений выбрать наибольшее и наименьшее.

Пример № 19. Требуется изготовить закрытый цилиндрический бак. объёмом 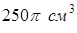. Каким должны быть его размеры, чтобы на его изготовление пошло наименьшее количество материала.

Решение: Здесь требуется определить радиус основания R и высоту Н цилиндра, чтобы при заданном объёме площадь его полной поверхности была наименьшей. Площадь полной поверхности цилиндра вычисляется по формуле: 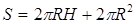Наименьшее значение этой функции и следует определить. Так как S является функцией двух независимых переменных, то одну из них надо исключить. Известно, что объём цилиндра 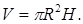или 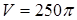. Выразим Н через V: 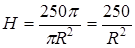тогда , .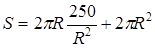

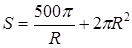1. Областью определения функции S являются положительные значения радиуса, то есть .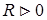

2. Находим производную: 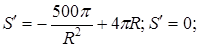при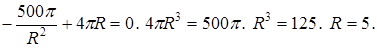

3. Находим вторую производную: 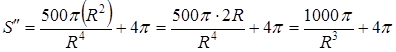Так как 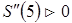, то при R=5 имеет место минимум функции S, который и является наименьшим значением функции S. Тогда: 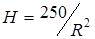, или 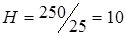. Итак, на изготовление цилиндрического бака пойдёт наименьшее количество материала, если длина радиуса основания цилиндра равна 5 см., а высота цилиндра 10 см.

Пример № 20. Требуется изготовить ящик с крышкой стороны основания которого относятся как 1:2, а площадь полной поверхности 108 см². Каким должны быть его размеры, чтобы его объём был наибольшим?

Решение: Здесь требуется определить стороны основания a и b и высоту Н прямоугольного параллелепипеда, чтобы при заданной площади полной поверхности его объём был наибольшим.

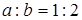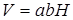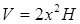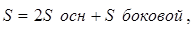
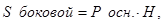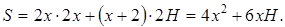
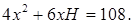
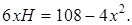
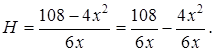
По условию, , откуда а=х, b=2х. Объём прямоугольного параллелепипеда равен: или . Надо исключить переменную Н. Известно, что S=108 и Имеем 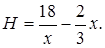Тогда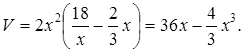

Наибольшее значение этой функции и следует определить:

1. Областью определения функции V являются положительные значения х, то есть .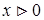

2. Находим производную: 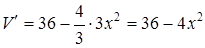, 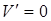при 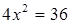, х²=9, х=3.

3. Находим вторую производную: 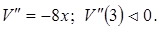то есть х=3. Функция имеет максимум, который и служит наибольшим значением функции. При этом: 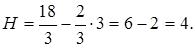Итак, объём ящика является наибольшим, если стороны его основания имеют длину 3 и 6 см., а высота 4 см.

Пример № 21: Число 10 разбить на два положительных слагаемых так, чтобы сумма их кубов была наименьшей.

Решение: Пусть одно из слагаемых равно х, тогда другое слагаемое есть 10-х. Сумма кубов этих слагаемых равна: ,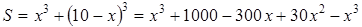

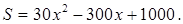
Наименьшее значение этой функции и надо определить:

1. Областью определения функции S является положительное значение х, то есть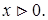

2. Находим производную: 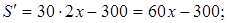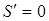при 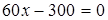, , 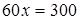х=5.

3. Находим вторую производную: 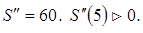то есть при х=5 функция S имеет минимум, который и является наименьшим значением функции. Итак, число 10 надо разложить на два равных слагаемых: 5и 5.