Теорема умножения вероятностей для n событий.
Вероятность произведения n событий А1 +Аn равна

где  - вероятность появления события Ak, при условии что события
- вероятность появления события Ak, при условии что события  в данном опыте произошли.
в данном опыте произошли.
Доказательство.
Используем метод математической индукции.
Однако для экономии времени и места докажем переход от m сомножителей к m +1 для случая m = 2. Докажем, что
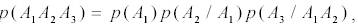
если

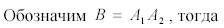
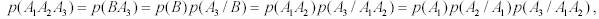
что и требовалось доказать.
Если события А1 +Аn независимы, то вероятность произведения равна произведению вероятностей этих событий:
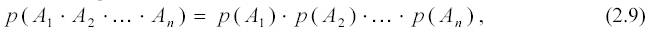
а вероятность появления хотя бы одного события А1, А2,..., Аn равна (см. (2. 4))
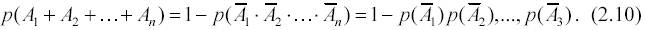
3.6. Решение типовых задач.
Пример 1.
Найти вероятность выпадения герба (событие А) при бросании монеты.
Решение.
Общее число равновозможных случаев n = 2 — орел и решка.
Число благоприятствующих случаев (появление орла) равно m = 1.
Тогда вероятность выпадения герба равна: Р(А)=1/2.
Пример 2.
Найти вероятность выпадения грани с цифрой 3 (три очка) (событие А) при однократном бросании шестигранной игральной кости.
Решение.
Число п=6 (по числу граней кубика); та=1 (выпадение цифры 3).
Вероятность появления цифры 3 равна: Р(А)=1/6
Пример 3.
Найти вероятность наступления события А, которое заключается в выпадении не менее 3 очков при однократном бросании игральной кости.
Решение.
Как и в предыдущем примере, общее число равновозможных случаев n = 6;
число случаев благоприятствующих ma=4, поскольку интересующему нас событию (выпадение не менее 3 очков) удовлетворяют случаи выпадения 3, 4, 5 и 6 очков. Следовательно, вероятность выпадения не менее 3 очков равна:
Р(А) = 4/6 = 2/3
Пример 4.
В урне находится 10 шаров, из них 3 красных и 7 синих. Найти вероятность того, что взятые наугад два шара оба окажутся красными.
Решение.
В данном примере общее число равновозможных случаев равно числу сочетаний из всего числа шаров по два n = C210 поскольку любые два шара могут быть вынуты с равными шансами. Число благоприятствующих случаев равно числу сочетаний из числа красных шаров по два ma = C23, ибо только такие сочетания удовлетворяют требованию выбора двух красных шаров.
Следовательно,
P(A) = C23 / C210 =3 / 45 = 1 / 15
Пример 4.
В ящике m белых и n черных шаров. Шары тщательно перемешаны. Наудачу вынимают сразу два шара.
Какова вероятность того, что оба вынутые шара белые?
Решение.
#G0 Вариант 1.
1.Пронумеруем шары (от 1 до m + n).
2. Так как порядок появления шаров неважен (он не указан), то общее число возможных комбинаций равно 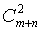 .
.
3. Пусть А - событие, когда оба шара белые. Тогшда число таких комбинаций равно 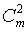 .
.
4. По формуле определения классической вероятности находим: 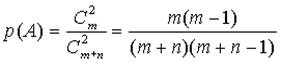 .
.
Вариант 2.
1. События - оба шара белые и 1ый и 2ой шары белые - совпадают. Достаточно вычислить вероятность события, которое представляет собой произведение событий: А = {вынутый первый шар является белым}, B = { вынутый второй шар является белым}
2. 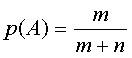 и, поскольку, если событие А произошло, то в ящике осталось n+m-1 шаров, среди которых m-1 белых, и вероятность снова вынуть белый шар будет равна:
и, поскольку, если событие А произошло, то в ящике осталось n+m-1 шаров, среди которых m-1 белых, и вероятность снова вынуть белый шар будет равна:  .
.
3. Воспользуемся формулой произведения вероятностей: 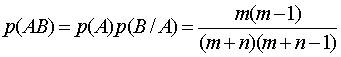 .
.
Пример 5.
В партии из10 деталей 7 стандартных.
Найти вероятность того, что среди 6ти взятых наугад деталей - 4 стандартных.
Решение.
1. Общее число возможных элементарных исходов испытания(опыта)равно числу способов, которыми можно извлечь 6 деталей из 10,т.е.
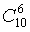
2. Общее число исходов, благоприятствующих интересующему нас событию А равно: 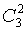
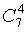 .
.
3. Искомая вероятность 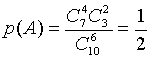 .
.
Пример 6.
Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово "кукла"?
Решение.
Используем классическое определение вероятности: P=m/n, где n - число всех возможных элементарных исходов, m - число элементарных исходов, благоприятствующих осуществлению события, заключающегося в том, что ребенок соберет из кубиков слово «Кукла».
Число различных перестановок из букв (элементов) множества { А, К, К, Л, У}равно 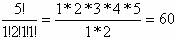 , из них только одна соответствует слову "кукла" (m=1), поэтому вероятность того, что ребенок соберет из кубиков слово "кукла" равна P=1/60.
, из них только одна соответствует слову "кукла" (m=1), поэтому вероятность того, что ребенок соберет из кубиков слово "кукла" равна P=1/60.
Ответ: 1/60.
Пример 7.
Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
Решение.
Пусть 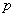 - вероятность попадания в цель при одном выстреле. Введем событие X = {при четырех выстрелах есть хотя бы одно попадание} и противоположное ему событие
- вероятность попадания в цель при одном выстреле. Введем событие X = {при четырех выстрелах есть хотя бы одно попадание} и противоположное ему событие 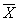 = {при четырех выстрелах нет ни одного попадания}.
= {при четырех выстрелах нет ни одного попадания}.
Вероятность события 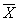 равна
равна 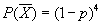 , тогда вероятность события Х равна
, тогда вероятность события Х равна  . По условию эта вероятность равна 0,9984, откуда получаем уравнение относительно
. По условию эта вероятность равна 0,9984, откуда получаем уравнение относительно 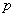
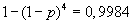
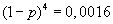
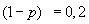

Ответ: 0,8.
Пример 8.
.
Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе - 0,9, в третье - 0,8. Найти вероятность следующих событий:
а) только одно отделение получит газеты вовремя;
б) хотя бы одно отделение получит газеты с опозданием.
Решение.
Введем события
А1 = (газеты доставлены своевременно в первое отделение),
А2 = (газеты доставлены своевременно во второе отделение),
А3 = (газеты доставлены своевременно в третье отделение),
по условию P(A1)=0,95; P(A2) = 0,9; P(A3)=0,8.
Найдем вероятность события Х = (только одно отделение получит газеты вовремя). Событие Х произойдет, если
или газеты доставлены своевременно в 1 отделение, и доставлены не вовремя во 2 и 3,
или газеты доставлены своевременно в 2 отделение, и доставлены не вовремя во 1 и 3,
или газеты доставлены своевременно в 3 отделение, и доставлены не вовремя во 2 и 1.
Таким образом, 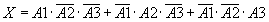
Так как события А1, А2, А3 - независимые, по теоремам сложения и умножения получаем
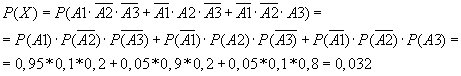
Найдем вероятность события У=(хотя бы одно отделение получит газеты с опозданием). Введем противоположное событие  =(все отделения получат газеты вовремя). Вероятность этого события
=(все отделения получат газеты вовремя). Вероятность этого события

Тогда вероятность события У:

Ответ: 0,032; 0,316.
3.7.Формулы полной вероятности, Байеса и Бернулли.
Следствием обеих теорем вероятности: теоремы сложения и теоремы умножения – является формула полной вероятности.
3.7.1.Формула полной вероятности.
Пусть проводится опыт, об условиях которого можно сделать n исключающих друг друга предположений (гипотез), образующих полную группу:

Каждая из гипотез осуществляется случайным образом и представляет собой случайное событие. Вероятности гипотез известны и равны:

Рассмотрим некоторое событие А, которое может появиться только
вместе с одной из гипотез. Известны условные вероятности события А для каждой из гипотез:
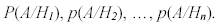
Требуется определить полную (безусловную) p(А) вероятность события А.
Представим событие А как сумму из n несовместимых вариантов:
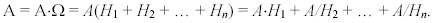
На основании второй аксиомы
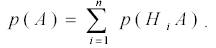
С учетом теоремы умножения вероятностей 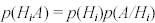

3.7.2.Формула Байеса.
Базируется на формуле полной вероятности и теореме умножения вероятностей.
Пусть до проведения некоторого опыта об его условиях n можно сделать n исключающих друг друга предположений (гипотез), образующих полную группу:
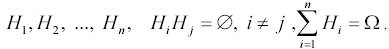
Вероятности гипотез до опыта (априорные вероятности) известны:
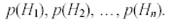
Опыт произведен, и произошло некоторое событие А. Требуется определить вероятности гипотез с учетом того, что произошло событие А, т.е.определить апостериорные вероятности:

Вероятность того, что событие А произошло совместно с Нi, на основании теоремы умножения вероятностей равна 
Отбросим левую часть равенства и выразим 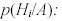
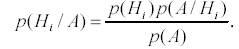
Раскроем p(A) по формуле полной вероятности (3.1) и получим формулу Байеса
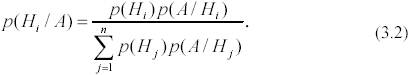
Формула Байеса позволяет пересчитать априорные вероятности гипотез с учетом того, что опыт завершился событием А.
3.7.3.Формула Бернулли.
Теорема о повторении опытов
Пусть проводятся n независимых одинаковых опытов, в каждом из которых событие А появляется с вероятностью р.
Вероятность P(n, k) того, что событие А произойдет ровно в k опытах, равна (формула Бернулли):
где q = 1 – р – вероятность того, что А не появится в одном опыте.
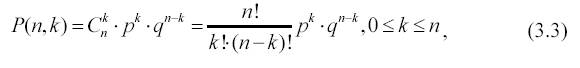
Свойства формулы Бернулли:
1. Правая часть формулы (3.3) представляет собой общий член разложения бинома Ньютона:

2. Рекуррентная формула P(n, k)имеет вид
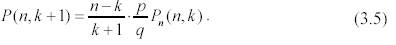
3. Число к0, которому соответствует максимальная вероятность P (n, k0), называется наивероятнейшим числом появления события А и определяется неравенствами

Вычисление вероятностей P (n,k) при больших значениях n по формуле Бернулли проблематично. Поэтому вычисление соответствующих вероятностей проводится с помощью следующих приближенных формул.
Если количество испытаний велико 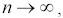 а вероятность события мала
а вероятность события мала 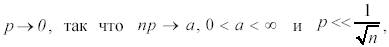
то используется формула Пуассона:
 (3.7)
(3.7)
Если количество испытаний n велико, вероятности p и q не малы, так что выполняются следующие условия:
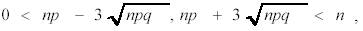 то применяются приближенные формулы Муавра–Лапласа:
то применяются приближенные формулы Муавра–Лапласа:
– локальная
 (3.8)
(3.8) 
– интегральная
 (3.9)
(3.9) 

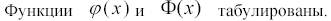
При использовании таблиц следует помнить, что 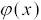 . является четной
. является четной  а функция Лапласа – нечетной
а функция Лапласа – нечетной
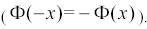
3.8.Дискретные и непрерывные случайные величины.
Под случайной величиной (СВ) понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение, причем заранее, до опыта, неизвестно, какое именно.
Случайные величины будем обозначать большими буквами:  их значения – соответствующими малыми буквами: x, y, z, а
их значения – соответствующими малыми буквами: x, y, z, а
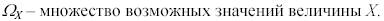
Примеры случайных величин:
1. Опыт – бросок одной игральной кости; случайные величины Х – число выпавших очков; 
2. Опыт – работа ЭВМ до первого отказа; случайные величины X – время наработки на отказ; 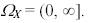
В зависимости от вида множества 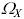 случайные величины могут быть дискретными и непрерывными.
случайные величины могут быть дискретными и непрерывными.
Случайная величина (СВ) Х называется дискретной, если множество 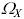 – счетное, т.е. его элементы можно расположить в определенном порядке и пронумеровать.
– счетное, т.е. его элементы можно расположить в определенном порядке и пронумеровать.
Случайная величина Х называется непрерывной (недискретной), если множество 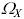 – несчетное.
– несчетное.
Законом распределения случайной величины Х называется любая функция (правило, таблица и т.п.), устанавливающая соответствие между значениями случайной величины и вероятностями их наступления и, позволяющая находить вероятности всевозможных
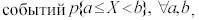 связанных со случайной величиной.
связанных со случайной величиной.
3.9. Законы распределения дискретной случайной величины.
Функцией распределения F(x) случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x:



Многоугольник вероятностей есть графическое изображение ряда
распределения вероятностей. По оси абсцисс откладываются возможные
значения случайной величины, а по оси ординат – вероятности этих значений.
Для наглядности полученные точки соединяются отрезками прямых.
Многоугольник распределения, так же как и ряд распределения, полностью
характеризует случайную величину и является одной из форм закона
распределения.
Функция распределения любой дискретной случайной величины есть
разрывная ступенчатая функция, скачки которой происходят в точках,
соответствующих возможным значениям случайной величины, и равны
вероятностям этих значений:
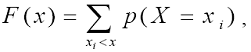
где суммирование распространяется на все значения xi, которые меньше х.
Плотность распределения
Случайная величина Х называется непрерывной, если ее функция распределения F (x) – непрерывная и дифференцируемая функция для всех
значений аргумента.
Для непрерывной функции распределения F (x) вероятность любого
отдельного значения случайной величины должна быть равна нулю, т.е. не
должно быть скачков ни в одной точке. Это аналогично телу, имеющему определенную массу, но ни одна из точек внутри тела конечной массой не обладает. Малый объем обладает конечной массой, но она приближается к нулю по мере уменьшения объема и в пределе равна нулю для точки. То есть при
непрерывном распределении вероятностей вероятность попадания на сколь
угодно малый участок отлична от нуля, тогда как вероятность попадания в строго определенную точку в точности равна нулю.
Вероятность попадания непрерывной случайной величины X на участок от
x до x + Δ x равна приращению функции распределения на этом участке:
p { x ≤ X < x + Δ x } = F (x + Δ x) – F (x). Тогда плотность вероятности на этом
участке равна 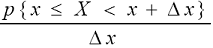 .
.
. Переходя к пределу при Δ x → 0, получим плотность вероятности в точке x: 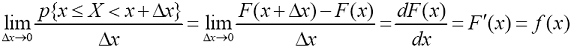
Полученная функция является одной из форм закона распределения
непрерывных случайных величин.
Плотностью распределения (плотностью вероятности) f (x) непрерывной
случайной величины X называется производная ее функции распределения

а график плотности распределения называется кривой распределения.
Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность
попадания случайной величины X на этот интервал равна f (x) dx. Эта величина
называется элементом вероятности. Вероятность попадания случайной
величины X на произвольный участок [ a, b [ равна сумме элементов вероятности
на этом участке:
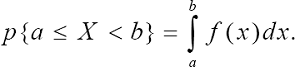
В геометрической интерпретации p { a ≤ X < b } равна площади, ограниченной сверху кривой плотности распределения f (x) и участком [ a, b [.
Соотношение () позволяет выразить функцию распределения F (x) случайной величины X через ее плотность:
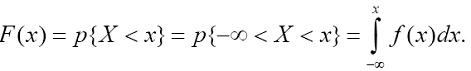
Основные свойства плотности распределения:
1. Плотность распределения неотрицательна f (x) ≥ 0, так как ее первообразная F (x) является неубывающей функцией (см. свойство 3 F (x)).
2. Условие нормировки: f (x) dx p (X) 1.

Полная площадь, ограниченная кривой распределения и осью абсцисс,
равна 1.
3.10. Типовые законы распределения дискретной случайной величины.
Геометрическое распределение имеет дискретная случайная величина Х,
если она принимает значения 0, 1, …, ∞ с вероятностями:
P(X=i) = 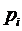 =
= 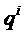 P (3.)
P (3.)
где p – параметр распределения (0 ≤ p ≤ 1), q= 1 – p.
Числовые характеристики геометрического распределения:
M[X] = q/p; D[X] = q/ 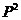 (3.)
(3.)
Условия возникновения. Проводится ряд одинаковых независимых опытов
до первого появления некоторого события А. Случайная величина Х – число
проведенных безуспешных опытов до первого появления события А.
Биномиальное распределение имеет дискретная случайная величина X,
если она принимает значения 0, 1, …, n со следующими вероятностями:
P(X=i) = 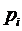 =
=  (3.)
(3.)
где n, p – параметры распределения (0 ≤ p ≤ 1), q = 1 – p.
Числовые характеристики биномиального распределения:
M[X] = np; D[X] = nqp (3.)
Условия возникновения. Проводится n одинаковых независимых, в каждом
из которых событие А появляется с вероятностью р. Случайная величина Х –
число опытов, в которых произошло событие А.
Распределение Пуассона имеет дискретная случайная величина Х, если
она принимает значения 0, 1, …, ∞ со следующими вероятностями:
P(X=i) = 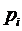 =
=  (3.)
(3.)
где a – параметр распределения (a > 0).
Числовые характеристики пуассоновской случайной величины:
M[X] = a; D[X] = a (3.)
Условия возникновения:
1. Распределение Пуассона является предельным случаем биномиального,
когда число опытов n неограниченно увеличивается, а вероятность p события A
в одном опыте стремится к 0.
2. Случайная величина Х – число событий пуассоновского потока, поступивших в течение интервала τ, причем параметр а = τλ, где λ – интенсивность потока.
Поток случайных событий называется пуассоновским или простейшим, если он является стационарным, ординарным и без последействия.
Поток случайных событий называется стационарным, если число событий, приходящихся на интервал τ, в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени λ
(интенсивность потока) постоянно.
Поток случайных событий называется ординарным, если вероятность попадания в некоторый участок Δ t двух и более случайных событий значительно меньше, чем вероятность попадания 1-го события.
В потоке отсутствует последействие, если вероятность попадания событий на участок τ не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.
Равномерное распределение имеет непрерывная случайная величина Х,
если ее плотность вероятности в некотором интервале [ а; b ] постоянна, т.е. если
все значения X в этом интервале равновероятны:
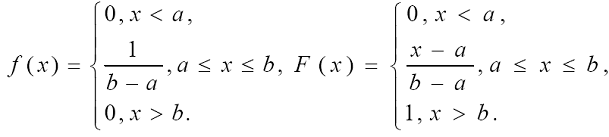
Ниже приведены графики плотности и функции равномерного распределения
при b = 3 и a = 1.
Числовые характеристики равномерно распределенной случайной
величины:

При необходимости определения параметров a и b по известным mX, DX
используют следующие формулы:

Условия возникновения:
1. Случайная величина Х – ошибки округления при ограниченной разрядной сетке:
– округление до меньшего целого, X ∈ [–1; 0], mX = – 0,5;
– округление до большего целого, X ∈ [–0; 1], mX = 0,5;
– округление до ближайшего целого, X ∈ [– 0,5; 0,5], mX = 0,
где 1 – вес младшего разряда.
2. Случайная величина Х – погрешность считывания значений с аналоговой шкалы измерительного прибора, X ∈ [– 0,5; 0,5], mX = 0, где 1 – цена деления шкалы.
3. Генераторы псевдослучайных величин, например RANDOM, встроенные в языки программирования высокого уровня.
Экспоненциальное распределение имеет непрерывная случайная величина T, принимающая только положительные значения, если ее плотность вероятности и функция распределения равны:
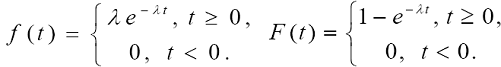
где λ – параметр распределения (λ > 0).
Ниже приведены графики плотности и функции экспоненциального
распределения при λ = 1 (см.рис.3.)

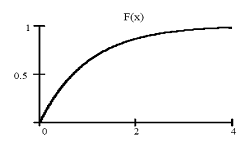
Рис.3.
Числовые характеристики экспоненциальной случайной величины:
M[T]= 1/λ; D [T]= 1/  . (3)
. (3)
Условия возникновения. Случайная величина T – интервал времени между двумя соседними событиями в простейшем или пуассоновском потоке случайных событий, причем параметр распределения λ – интенсивность потока.
Нормальное распределение (распределение Гаусса) имеет непрерывная
случайная величина Х, если ее плотность вероятности и функция распределения
равны:
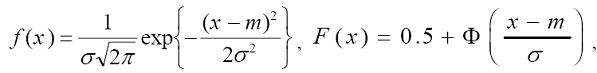
где m, σ – параметры распределения (σ > 0); 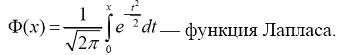
Ниже приведены графики плотности и функции нормального распределения при m = 1, σ = 1.


Рис.3.
Для вычисления значений функции распределения и вероятностей событий,
связанных с нормальной случайной величиной, используется табулированная
функция Лапласа. При использовании таблицы значений функции Лапласа
следует учитывать, что Φ(– x) = – Φ(x), Φ(0) = 0, Φ(∞) = 0,5.
Числовые характеристики нормальной случайной величины:
M[X] = m; D[X} = 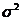 (3)
(3)

Условия возникновения. Это наиболее часто встречающийся на практике закон распределения. Например, нормальный закон распределения имеют:
– погрешности измерительных приборов; при этом откалиброванный прибор не имеет систематической погрешности, т.е. m = 0, а величина σ определяется классом точности измерительного прибора;
– параметры радиоэлектронных компонентов (резисторов, конденсаторов и т.п.), причем m – номинальное значение, указанное на маркировке, а σ определяется классом точности.
3.11. Основные числовые характеристики дискретной случайной величины.
Закон распределения случайной величины является исчерпывающей характеристикой, которая полностью описывает случайную величину с вероятностной точки зрения. Однако во многих практических задачах нет надобности в таком полном описании и достаточно указать только отдельные числовые параметры, характеризующие существенные черты распределения.
Такие числа называются числовыми характеристиками случайной величины.
Математическое ожидание характеризует среднее значение случайной величины и определяется по формулам:
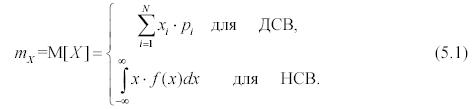
где mX обозначает число, полученное после вычислений по формуле (5.1);
M[X] – оператор математического ожидания.
Как видно из (5.1), в качестве математического ожидания используется «среднее взвешенное значение», причем каждое из значений случайной величины учитывается с «весом», пропорциональным вероятности этого значения.
Физический смысл математического ожидания – среднее значение случайной величины, т.е. то значение, которое может быть использовано
вместо случайной величины в приблизительных расчетах или оценках.
Математическое ожидание обладает следующими свойствами:
1. M[c] = c.
Доказательство. Рассмотрим константу c как случайную дискретную величину, которая принимает одно значение c с вероятностью р = 1.
2. 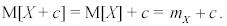
Доказательство:

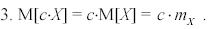
Доказательство:
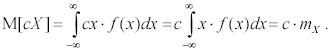
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и определяется по формулам:
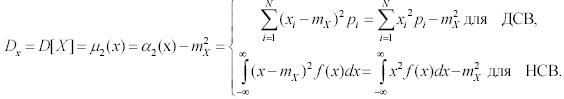
Свойства дисперсии:


К ним можно отнести моду,медиану и квантиль.
3.12. Упражнение к главе 3.
Задача 1.
Два охотника одновременно и независимо стреляют в кабана.Известно, что первый охотник попадает в цель с вероятностью р= 0,8, а второй - с вероятность 0,4. Кабан убит, и в нем обнаружена одна пуля.
Как делить кабана?
Делить кабана следует пропорционально условным вероятностям попадания каждого охотника при условии, что в кабане только одна пуля.
Пусть А - событие,котолрое заключается в том,что в кабане имеется одна пуля.
Выберем полную группу событий:
1) не попал ни первый охотник,ни второй -  .
.
2) попал первый,не попал второй - 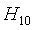 .
.
3) не попал первый, попал второй - 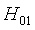 .
.
4) попал и первый и второй - 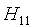 .
.
Необходимо найти условные вероятности  и
и 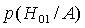 ,так очевидно, что из 4х событий, только эти два являются достоверными:в кабане имеется одна пуля и оба охотника стреляли в него.
,так очевидно, что из 4х событий, только эти два являются достоверными:в кабане имеется одна пуля и оба охотника стреляли в него.
По формулам умножения вероятностей независимых событий имеем:
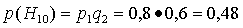 и
и 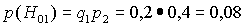 , где
, где  - вероятность попадания первого охотника,
- вероятность попадания первого охотника, 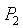 - вероятность попадания второго охотника;
- вероятность попадания второго охотника;  - вероятность промаха первого охотника,
- вероятность промаха первого охотника,  - вероятность промаха второго охотника.
- вероятность промаха второго охотника.
Применяя формулу Байеса  , где i не равно j,
, где i не равно j, 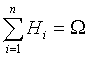 и
и  О
О
получим:


Говоря иными словами, кабана следует разделить в отношении
6:1.
Задача 2.
Вероятность попадания в цель при каждом выстреле из лука равна 1/3. Производится 6 выстрелов.
Какова вероятность ровно 2х попаданий?
Обозначим событие А = { попадание при одном выстреле}, p = p(A) = 1/3; q = 1 - p = 2/3. Число выстрелов n = 6.
Считаем, что выстрелы не зависят друг от друга.
Тогда ответ на первый вопрос находим по формуле Бернулли:
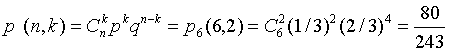
И так, вероятность ровно 2х попаданий близка к 1/3.
Задача 3.
Среди 100 лоторейных билетов есть 5 выйгрышных. Найти вероятность того, что 2 выбранных наудачу билета окажутся выйгрышными.
Введем обозначения событий:
А - 1ый билет оказался выйгрышным.
В - 2ой билет оказался выйгрышным.
Тогда, вероятность того,что:
1ый билет окажется выйгрышным р(А) = 1/5 = 0,2.
2ой билет окажется выйгрышным р(В) = 1/4 = 0,25 (при условии, что произошло событие А).
Искомая вероятность того, что 2 выбранных наудачу билета окажутся выйгрышными равна:
р(АB) = р(А)р(В) = 0,2 х 0,25 = 0,05 (при условии, что вероятность выйгрыша р = 5/100 = 0,05 - см.условие задачи).
И окончательно, р(АB) = р(А)р(В)р = 0,05 х 0,05 = 0,0025.
Задача 4.
В читальном зале имеется 6 учебников по Теории вероятностей, из которых 3 в переплете. Библиотекарь взял наугад 2 учебника.
Найти вероятность того, что оба учебника окажутся в переплете.
Пусть событие А заключается в том,что 1ый взятый учебник имеет переплет, а событие В заключается в том,что 2ый взятый учебник тоже имеет переплет.
Тогда р(А) = 3/6 = 0,5.
А условная вероятность р(В) = 2/5 = 0,4 (при условии,что событие А произошло.
Искомая вероятность р(АВ) = р(А)р(В) = 0,5 х 0,4 = 0,2.
Задача 5.
Найти математическое ожидание дискрентой случайной величины (ДСВ) Х, заданной законом распределения:
Х = - 4, 6, 10 соответственно р = 0,2, 0,3, 0,5.
По формуле для математического ожидания ДСВ находим:
М(Х) = х1р1 + х2р2 + х3р3 = (-4)0,2 + 6 (0,3) + 10 (0,5) = 6
Задача 6.
Среди приведенных таблиц распределения дискретной случайной величины X есть две неверные (невозможные).
Найдите эти таблицы.
Таблица 1
Ответ: таблицы 2 и 4.
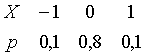
Таблица 2
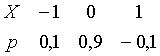
Таблица 3
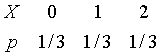
Таблица 4

Таблица 5
