Глава 4. Обоснование целесообразности использования методов генетических алгоритмов к задачам организационного проектирования
В рамках четвертой главы диссертации решается следующая задача – обоснование целесообразности применения методов генетических алгоритмов к задачам организационного проектирования.
Для решения этой задачи необходимо выполнить следующие шаги:
- провести краткий обзор и анализ методов моделирования, используемых при организационном проектировании;
- показать необходимость использования дополнительного метода;
- предложить в качестве такого метода – метод генетических алгоритмов и описать принципы его работы;
- провести анализ возможностей применения методов генетических алгоритмов на примере постановки и решения задач организационного проектирования;
- выявить сравнительные преимущества методов генетических алгоритмов.
Решение этих задач позволит обосновать применение методов генетических алгоритмов к решению задач организационного проектирования.
Анализ методов моделирования используемых при организационном проектировании
Проведенный нами обзор и анализ научной литературы [30,41,47,57,60] показал, что можно выделить две основные группы моделей, которые используются наиболее часто. Это математико-кибернетические и графо-аналитические модели.
В математико-кибернетических моделях используются три основные группы методов: методы математического программирования, методы исследования операций, методы экономической кибернетики. В таблице 14 представлены основные методы, используемые в математико-кибернетических моделях.
Таблица 14
Основные методы, используемые в математико-кибернетических моделях
|
|
| Группы методов | Методы |
| Методы математического программирования | Линейное программирование |
| Блочное программирование | |
| Нелинейное программирование | |
| Динамическое программирование | |
| Методы исследования операций | Методы решения линейных программ |
| Управление запасами | |
| Износ и замена оборудования | |
| Теория игр | |
| Теория расписания | |
| Сетевые методы планирования и управления | |
| Теория массового обслуживания | |
| Методы экономической кибернетики | Системный анализ |
| Методы имитационного моделирования | |
| Методы распознавания образов |
В графо-аналитических моделях используются различные методы, отображающие распределения функций, полномочий, ответственности, организационных связей в сетевом, матричном и других табличных и графических видах.
Методы математического программирования и исследования операций ориентированы на решение оптимизационных задач, поиск экстремума функции при заданных ограничениях. Для организационного проектирования они хорошо подходят для решения локальных задач оптимизации, таких как: структура капитала, транспортная задача, задача распределения ресурсов, задачи назначения.
Преимущества методов математического программирования и исследования операций состоят в следующем.
1. Эти методы дают оптимальные решения.
2. Легко применяются к широкому классу сравнительно простых, но необходимых задач.
3. Имеется большой накопленный объем типовых задач и решений.
Недостатки методов математического программирования и исследования операций [47,57,60,95,101]:
|
|
1. Низкая гибкость и адаптивность.
2. Не дает наглядного представления о системе (кроме сетевых).
3. Сильно зависит от сложности экономической составляющей задачи.
4. Ограничения на возможные комбинации ключевых параметров.
5. Высокие требования к уровню математической подготовки.
Методы экономической кибернетики основаны на применении системного подхода и его формальных процедур к созданию математической модели исследуемого объекта.
Обобщенно, методы экономической кибернетики воссоздают функционально-технологическую структуру компании. На входе и выходе получаются формализованные параметры, а сама структура модели – совокупность операций или процессов, где содержимое «черного ящика» представляет собой функциональные зависимости, преобразующие входные параметры в выходные. В некоторых случаях, подобное представление данных схоже с моделью нейронной сети.
|
|
 |  |
… …
 |  |
Xn Yn
 |  |
Рисунок 4 – Имитационная модель системы
В простейшем виде имитационная модель системы представлена на рисунке 4.
Элементы X1,…,Xn называются входами системы (входными переменными), Y1,…,Yn – выходами системы (выходными переменными), Z1, Z2, …, Zl характеризуют состояние системы. Символы a1, a2, …, ak обозначают параметры системы. Как видно из рисунка, имитационная модель в чем-то аналогична операционному представлению системы.
Преимущества методов экономической кибернетики.
|
|
1. Разработка кибернетической модели зачастую позволяет лучше понять реальную систему.
2. В ходе моделирования возможно сжатие времени: годы эксплуатации можно промоделировать в течение нескольких секунд.
3. Моделирование не требует прерывания текущей деятельности системы.
4. Кибернетические модели носят общий характер, в отличие от математических методов, их можно использовать там, где формальное математическое решение затруднено или невозможно.
5. Моделирование можно использовать в качестве средства обучения персонала работе системы.
6. Моделирование обеспечивает более точное воспроизведение свойств системы, чем математический анализ.
7. Моделирование подходит для переходных процессов, математические модели очень сложно адаптировать под этот класс задач.
8. Существуют много готовых моделей и компьютерных программ.
9. Дают ответ на вопрос «а что, если»?
Недостатки методов экономической кибернетики [67].
1. Создание кибернетической модели даже в рамках использования системного языка и простейших математических методов требует много времени и труда, при этом не дает гарантии результата.
2. Невозможно создать модель идентичную системе, полученные решения далеко не всегда наилучшие, или достаточно хорошие.
3. Моделирование сложных систем требует очень много времени.
4. Моделирование основано чаще всего на вероятностях и это уже несет субъективность, предпочтительнее однозначные модели, которые близки к методам математического программирования и графо-сетевым.
5. Для сложных моделей требуется много компьютерного времени на обработку.
6. Пока очень мало стандартизованных подходов, разные исследователи предлагают разные способы.
7. Зависит от сложности экономической составляющей задачи.
8. Необходимость согласования законов распределения и аналогичные трудности.
Графо-сетевые методы перечислены ранее в пункте 3.1.2. К ним следует добавить соответствующие методы, используемые при оптимизации бизнес-процессов, например метод структурного анализа процессов. По своим характеристикам они находятся между методами математического программирования и имитационными моделями. Совмещая в себе ряд достоинств и недостатков обоих.
Анализ перечисленных методов показал, что для полноценного моделирования организационных структур обычно применяют экономико-кибернетическое моделирование, дополняя решение отдельных частных вопросов методами математического программирования и исследования операций. Для наглядного представления используют графо-аналитические методы.
Совместное использование рассмотренных методов компенсирует ряд присущих им недостатков, однако следующие недостатки характерны для всех перечисленных методов.
1. Низкая гибкость и адаптивность формализованной составляющей.
2. Сильное ограничение возможных комбинаций ключевых параметров модели.
3. Сильная зависимость от сложности экономической составляющей задачи.
Очевидно, необходимы методы, которые позволят избавиться от этих недостатков. В качестве таких методов, которые упростят сложные расчеты, были предложены методы генетических алгоритмов (ГА).
4.2. Генетические алгоритмы: основные понятия, операторы, базовый алгоритм
4.2.1. Общие представления о генетических алгоритмах. Генетические алгоритмы, являясь одной из парадигм эволюционных вычислений, представляют собой алгоритмы поиска, построенные на принципах, сходных с принципами естественного отбора и генетики. Если говорить обобщенно, они объединяют в себе принцип выживания наиболее перспективных особей-решений и структуризированный обмен информацией, в котором присутствует элемент случайности, который моделирует природные процессы наследования и мутации. Дополнительным свойством этих алгоритмов является невмешательство человека в развивающийся процесс поиска. Человек может влиять на него лишь опосредованно, задавая определенные параметры.
Будучи разновидностью методов поиска, с элементами случайности, генетические алгоритмы имеют целью нахождение лучшего, а не оптимального решения задачи. Это связано с тем, что для сложной системы часто требуется найти хоть какое-нибудь удовлетворительное решение, а проблема достижения оптимума отходит на второй план. При этом другие методы, ориентированные на поиск именно оптимального решения, вследствие чрезвычайной сложности задачи становятся вообще неприменимыми. В этом кроется причина появления, развития и роста популярности генетических алгоритмов. Хотя, как и всякий другой метод поиска, этот подход не является оптимальным методом решения любых задач.
Преимущества генетических алгоритмов становятся еще более прозрачными, если рассмотреть основные их отличия от традиционных методов. Основных отличий четыре.
Первое. Генетические алгоритмы работают с кодами, в которых представлен набор параметров, напрямую зависящих от аргументов целевой функции. Причем интерпретация этих кодов происходит только перед началом работы алгоритма, и после завершения его работы для получения результата. В процессе работы манипуляции с кодами происходят совершенно независимо от их интерпретации, код рассматривается просто как битовая строка.
Второе. Для поиска генетический алгоритм использует несколько точек поискового пространства одновременно, а не переходит от точки к точке, как это делается в традиционных методах. Это позволяет преодолеть один из их недостатков - опасность попадания в локальный экстремум целевой функции, если она не является унимодальной, то есть имеет несколько таких экстремумов. Использование нескольких точек одновременно значительно снижает такую возможность.
Третье. Генетические алгоритмы в процессе работы не используют никакой дополнительной информации, что повышает скорость работы. Единственной используемой информацией может быть область допустимых значений параметров и целевой функции в произвольной точке.
Четвертое. Генетический алгоритм использует как вероятностные правила для порождения новых точек анализа, так и детерминированные правила для перехода от одних точек к другим. Выше уже говорилось, что одновременное использование элементов случайности и детерминированности дает значительно больший эффект, чем раздельное.
Прежде чем рассматривать непосредственно работу генетического алгоритма, введем ряд терминов, которые широко используются в данной области.
Выше было показано, что генетический алгоритм работает с кодами безотносительно их смысловой интерпретации. Поэтому сам код и его структура описываются понятием генотип, а его интерпретация, с точки зрения решаемой задачи, понятием фенотип. Каждый код представляет, по сути, точку пространства поиска. С целью максимально приблизиться к биологическим терминам, экземпляр кода называют хромосомой, особью или индивидуумом. Далее для обозначения строки кода мы будем в основном использовать термин "особь".
На каждом шаге работы генетический алгоритм использует несколько точек поиска одновременно. Совокупность этих точек является набором особей, который называется популяцией. Количество особей в популяции называют размером популяции. Поскольку в данном параграфе мы рассматриваем классические генетические алгоритмы, то можем сказать, что размер популяции является фиксированным и представляет одну из характеристик генетического алгоритма. На каждом шаге работы генетический алгоритм обновляет популяцию путем создания новых особей и уничтожения старых. Чтобы отличать популяции на каждом из шагов и сами эти шаги, их называют поколениями и обычно идентифицируют по номеру. Например, популяция, полученная из исходной популяции после первого шага работы алгоритма, будет первым поколением, после следующего шага - вторым, и т.д.
В процессе работы алгоритма генерация новых особей происходит на основе моделирования процесса размножения. При этом, естественно, порождающие особи называются родителями, а порожденные - потомками. Родительская пара, как правило, порождает пару потомков. Непосредственная генерация новых кодовых строк из двух выбранных происходит за счет работы оператора скрещивания, который также называют кроссовером (в русской литературе также кроссинговером) (от англ., crossover). При порождении новой популяции оператор скрещивания может применяться не ко всем парам родителей. Часть этих пар может переходить в популяцию следующего поколения непосредственно. Насколько часто будет возникать такая ситуация, зависит от значения вероятности применения оператора скрещивания, которая является одним из параметров генетического алгоритма.
Моделирование процесса мутации новых особей осуществляется за счет работы оператора мутации. Основным параметром оператора мутации также является вероятность мутации.
Поскольку размер популяции фиксирован, то порождение потомков должно сопровождаться уничтожением других особей. Выбор пар родителей из популяции для порождения потомков производит оператор отбора, а выбор особей для уничтожения - оператор редукции. Основным параметром их работы является, как правило, качество особи, которое определяется значением целевой функции в точке пространства поиска, описываемой этой особью.
Таким образом, можно перечислить основные понятия и термины, используемые в области генетических алгоритмов:
• генотип и фенотип,
• особь и качество особи,
• популяция и размер популяции,
• поколение,
• родители и потомки.
К характеристикам генетического алгоритма относятся:
• размер популяции,
• оператор скрещивания и вероятность его использования,
• оператор мутации и вероятность мутации,
• оператор отбора,
• критерий останова.
Операторы отбора, скрещивания, мутации называют еще генетическими операторами.
Критерием останова работы генетического алгоритма может быть одно из трех событий:
•Сформировано заданное пользователем число поколений.
•Популяция достигла заданного пользователем качества (например, значение качества всех особей превысило заданный порог).
•Достигнут некоторый уровень сходимости. То есть особи в популяции стали настолько подобными, что дальнейшее их улучшение происходит чрезвычайно медленно.
Характеристики генетического алгоритма выбираются таким образом, чтобы обеспечить малое время работы, с одной стороны, и поиск как можно лучшего решения, с другой.
4.2.2. Базовая структура генетического алгоритма. Кратко схема работы ГА представлена на рисунке 5.
Пояснить работу ГА можно следующей пошаговой схемой [7,100,101,102,103,109]:
1.Формирование начальной популяции P0 из v особей (a10,…,av0):
Генерация хромосомного набора из v бинарных строк Е(аkt), удовлетворяющих требованиям, предъявляемым к символьной модели исходной задачи.
Преобразование бинарных строк Е(аkt) в соответствующие им векторы управляемых переменных Хk Î D и вычисление степени приспособленности u(аkt) для каждой особи аi0, обладающей генотипом Е(Хi).
Особи аi0, k=1,…,v образуют начальную популяцию Рt для поколения t=0.
2. Воспроизводство потомков с наследными признаками родителей:
2.1. Выбор конкретной родительской пары (аkt, ait)ÎРt для участия в процессе размножения.
2.2. Выбор схемы размножения.
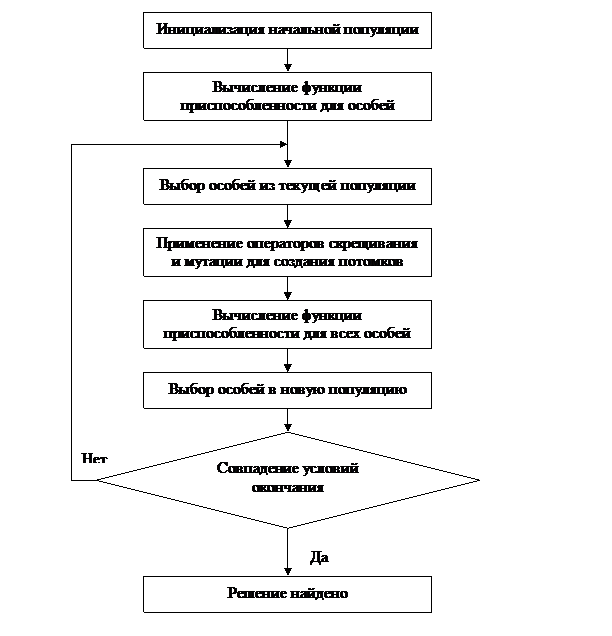
Рисунок 5 – Общая схема работы простого генетического алгоритма
2.3. Построение по выбранной схеме из генотипов родителей E(akt), E(ait) генотипов их потомков E(bit), i>=1, сохраняющих наследственные признаки родителей.
2.4. Преобразование бинарных строк E(bit) в соответствующие векторы управляемых переменных Хk Î D и вычисление степени приспособленности потомков, обладающих генотипами E(Xi).
2.5. Вычисления повторяются с шага 2.1. до тех пор, пока не будет воспроизведено заданное число потомков.
3. Мутагенез, приводящий к генетическим изменениям родительских признаков:
3.1. Выбор типа мутации.
3.2. Построение по генотипу E(akt) одной из особей akt Î Pt генотипа E(mit) генотипа особи мутанта mit с помощью конкретного типа мутации.
3.3. Преобразование бинарной строки E(mit) в соответствующий вектор управляемых переменных Xi Î D и вычисление степени приспособленности мутанта mit, обладающего генотипом E(Xi).
3.4. Вычисления повторяются с шага 3.1. до тех пор, пока не будет создано заданное число мутантов.
4. Естественный отбор:
4.1. Определение среди родителей, потомков и мутантов особей, образующих репродуктивную группу, которая примет участие в естественном отборе.
4.2. Выбор схемы естественного отбора.
4.3. Формирование по выбранной схеме хромосомного набора популяции следующего поколения Pt+1 = (a1t+1,…,avt+1) из особей, принадлежащих репродуктивной группе.
5. Проверка условий окончания процесса эволюции популяции P.
Если условия окончания процесса не выполнены, то происходит смена поколений и все вычисления для популяции следующего (t+1) – го поколения повторяются с шага 2.
В качестве условий окончания процесса эволюции популяции может использоваться одно из следующих неравенств:
t > T
или
Dб(t) = 0.
Выполнение неравенства t > T означает, что эволюция популяции закончена в связи с тем, что она исчерпала свой жизненный цикл; окончание эволюции популяции при равенстве побитового разнообразия текущей популяции Pt нулю означает, что все генотипы в хромосомном наборе популяции Pt совпадают между собой. Существуют и другие условия, например, когда хромосомный набор наиболее приспособленной особи не меняется в течение нескольких поколений; но подобные условия задаются в зависимости от типа решаемой задачи.
4.2.3. Символьная модель в общем представлении. Для реализации любого математического метода необходимо оговорить его символьное представление. В этом разделе оговариваются основы общей символьной модели, в следующих разделах ее представление для операторов отбора, скрещивания и мутации.
Конечное решение задачи обозначим как n - мерный вектор X = (х1,…,хn), X Î D, где D – область поиска решений. Каждая компонента xi, i = 1,…,n вектора X Î D может быть закодирована с помощью целого неотрицательного числа
bi Î [0,Ki], i=1,…,n,
где (Ki+1) – число возможных дискретных значений i – й управляемой переменной в области поиска D. Это позволяет поставить во взаимооднозначное соответствие каждому вектору X Î D вектор b с целочисленными компонентами
(x1,…,xn) «(b1,…,bn),
где для каждой компоненты bi, i = 1,…,n областью возможных значений являются целые числа от 0 до Ki.
Введем алфавит B2, содержащий только два символа 0 и 1: B2={0,1}. Для того чтобы представить целочисленный вектор b=(b1,…,bn) в алфавите B2 необходимо определить максимальное число двоичных символов q, которое достаточно для представления в двоичном коде любого значения bi из области его допустимых значений [0,Кi]. Нетрудно видеть, что параметр символьной модели q должен удовлетворять неравенству
К<2q,
где К = МАХ1≤i≤n(Кi).
Запись произвольного целого неотрицательного числа bi = (0≤bi≤2q) с помощью q двоичных символов определяется соотношением
bi = åqi=1 ai2q-i
где ai – двоичное число, равное 0 или 1; q-длина двоичного слова, кодирующего целое число bi.
В качестве гена – единицы наследственного материала, ответственного за формирование альтернативных признаков особи, примем бинарную комбинацию еq(bi), которая определяет фиксированное значение целочисленного кода bi управляемой переменной xi в обычном двоичном коде, тогда еq(bi) имеет вид:
| a1 | a2 | … | aq |
| q |
Одна особь akt будет характеризоваться n генами, каждый из которых отвечает за формирование целочисленного кода соответствующей управляемой переменной. Тогда хромосому можно определить в следующем виде E(X):
| ai1 | … | aq1 | ai2 | … | aq2 | … | … | … | ain | … | aqn |
| eq(b1) | eq(b2) | … | eq(bn) | ||||||||
| Ген 1 | ген 2 | … | ген n | ||||||||
| Локус 1 | локус 2 | … | Локус n | ||||||||
| ХРОМОСОМА |
Местоположение определенного гена в хромосоме называется локусом, а альтернативные формы одного и того же гена, расположенные в одних и тех же локусах, называются аллелями (аллелеформами).
Хромосому, содержащую в своих локусах конкретные значения аллелей, будем называть генотипом (генетическим кодом) E(akt), который содержит всю наследственную генетическую информацию об особи akt, получаемую от предков и передаваемую затем потомкам. Конечное множество всех допустимых генотипов образует генофонд.
Приняв в качестве внешней среды критерий оптимальности Q(X), мы можем говорить, что степенью приспособленности u(akt) каждой особи akt является численное значение функции Q(X), вычисленное для допустимого решения X особи с именем akt. В общем случае степень приспособленности u(akt) можно задать с помощью следующего выражения:
Q2(X), если решается задача максимизации функции Q(X)
u(akt) = {
1/(Q2(X)+1), если решается задача минимизации функции Q(X)
Фенотипом особи будем считать численные значения вектора управляемых переменных X Î D.
Необходимо отметить, что выбор символьной модели во многом определяет эффективность и качество применяемых генетических алгоритмов. Для каждого класса задач должна строиться своя символьная модель, отражающая специфику и особенности решаемой задачи.
4.2.4. Скрещивание [102]. Будем считать, что популяция Pt=(a1t,…,avt) представляет собой репродукционную группу – совокупность из v особей, любые две из которых akt,alt Î Pt, k¹1 могут размножаться, выступая в роли родителей (akt – мать; alt - отец). Здесь под размножением понимается свойство особей aktÎP воспроизводить одного или нескольких себе подобных непосредственных потомков (детей) bit, i ³ 1 и обеспечивать у них непрерывность и наследственную преемственность качественных признаков родителей.
Таким образом, этот фактор эволюционного развития популяции приводит к получению новой генетической информации, содержащей различные комбинации аллельных форм генов родительских генотипов.
В терминах задачи воспроизводство себе подобных можно интерпретировать как возможность построения по заданным допустимым решениям xk,xlÎD нового допустимого решения xiÎD, а непрерывность и наследственную преемственность – как возможность использования аллельных форм в виде бинарных комбинаций eq(bi) содержащихся в генотипах родителей E(xk) E(xl), для формирования генотипа E(xi) потомка, тем самым обеспечивая передачу наследственных признаков особей от поколения к поколению на уровне обмена генами.
Рассмотрим механизм размножения двух родительских особей akt,altÎP путем сигнамии (оплодотворения) их репродуктивных клеток – материнской гаметы (яйцеклетки) E(akt) и отцовской гаметы (сперматозоида) E(alt), каждая из которых является гаплоидом (одинарным набором непарных хромосом E(xk) и E(xl), соответственно).
В процессе сигнамии образуется родительская зигота – оплодотворенная клетка, способная развиваться в новую особь с передачей наследственных признаков (генетической информации) от родителей их потомкам. Зигота в отличие от гамет, является диплоидом, содержащим одну пару из двух неотличимых одна от другой хромосом, которые происходят от "родительских" гамет: одна от материнской гаметы, а другая от отцовской гаметы. Такие хромосомы называются гомологичными хромосомами. В гомологичных хромосомах для всех признаков имеется по два гена, называемых аллельными генами. Аллельные гены принадлежат одному и тому же локусу. В этом смысле локус принадлежит уже не отдельной хромосоме, а совокупности из двух гомологичных хромосом. Каждый локус содержит не менее двух аллелей, которые могут быть как одинаковыми, так и различными. Необходимо заметить, что гены родительских гамет могут существовать более чем в двух аллельных формах, хотя каждая зигота может быть носителем только двух форм аллелей (А или а).
Зиготы, содержащие в аллельных генах гомологичных хромосом одинаковые аллели (АА или аа), называются гомозиготами, а содержащие разные аллели (Аа или аА), называются гетерозиготами. Очевидно, что введенные понятия "гомозигота" и "гетерозигота" определяются относительно конкретного локуса, содержащего аллельный ген.
В результате акта сигнамии аллели родительских гамет могут поменяться местами в аллельных генах гомологичной хромосомы, что позволяет рассматривать следующие ситуация образования зигот:
| ЗИГОТЫ | |||||||||||||||
| Материнская хромосома | А | А | А | а | |||||||||||
| | ¯ | ↕ | - | ||||||||||||
| Отцовская хромосома | А | А | а | А | |||||||||||
| Гомозиготы | Гетерозиготы |
ген из отцовской хромосомы переходит в материнскую хромосому;
ген из материнской хромосомы переходит в отцовскую хромосому;
происходит взаимный обмен генами между материнской и отцовской хромосомами;
отцовская и материнская хромосомы остаются без изменения.
Таким образом, при образовании зигот происходит независимое и случайное расхождение родительских генов по аллельным генам гомологичных хромосом зиготы независимо от того, у какой из родительских гамет они присутствовали до оплодотворения.
Заключительным этапом размножения особей является акт мейоза - процесс образования гамет из родительской зиготы путем независимого расхождения гомологичных хромосом по дочерним гаметам, воспроизводящим потомство. Одна диплоидная зигота может дать начало четырем гаплоидным гаметам (гамете тождественно воспроизводящей отцовскую гамету; гамете, тождественно воспроизводящей материнскую гамету; гамете, являющейся отцовской гаметой, у которой в i-м локусе находится аллель i-го гена из материнской гаметы; гамете являющейся материнской гаметой, в которой в i-м локусе находится аллель i-го гена из отцовской гаметы).
Процесс размножения двух особей должен удовлетворять следующим законам наследственности Менделя.
1. Первому закону Менделя (закону расщепления) о наследовании альтернативных проявлений одного и того же признака, который формулируется следующим образом:
"Два гена, определяющие тот или иной признак, не сливаются и не растворяются один в другом, но остаются независимыми друг от друга расщепляясь, при формировании гамет".
Согласно этому закону гены (или соответствующие им признаки родителей), имеющие одинаковые аллели [eqOT(bi)=eqM(bi)], сохраняют свои значения в потомстве, т.е. передаются с вероятностью, равной 1, потомку по наследству. Гены родителей, имеющие разные аллели [eqOT(bi)¹eqM(bi)], передаются потомку по наследству с вероятностью, равной 0,5, т.е. половина гамет оказывается носителем аллели eqOT(bi), а другая половина - аллели eqM(bi).
2. Второму закону Менделя (закону независимого расщепления) о независимости комбинирования признаков, который формулируется следующим образом:
"Родительские гены, определяющие различные признаки, наследуются независимо друг от друга".
Согласно этому закону рекомбинация (обмен) генов в акте сигнамии может происходить либо в каком-то одном аллельном гене, либо в нескольких аллельных генах одновременно, т.е. передача аллелей от родителей потомству может происходить в каждом аллельном гене независимо друг от друга. При этом может оказаться, что гаметы потомков либо совпадают с родительскими гаметами, либо отличаются от них в одном или нескольких локусах.
На практике одним из наиболее распространенных является одноточечный кроссовер, когда произвольно или по какому-либо алгоритму выбирается одна точка разрыва и родительские хромосомы обмениваются “хвостами”.
Двухточечный кроссовер и равномерный кроссовер [7] - вполне достойные альтернативы одноточечному оператору. В двухточечном кроссовер выбираются две точки разрыва, и родительские хромосомы обмениваются сегментом, который находится между двумя этими точками. В равномерном кроссовере, каждый бит первого родителя наследуется первым потомком с заданной вероятностью; в противном случае этот бит передается второму потомку и наоборот.
4.2.5. Мутация [7]. В результате размножения воспроизводятся потомки, обладающие свойством преемственности наследственных признаков (генов) родителей. При этом генотипы потомков, как правило, содержат новые сочетания аллельных форм генов родителей, ведущие к новым количественным признакам потомков (фенотипу и степени приспособленности). Однако генетическая информация, содержащаяся в хромосомном наборе родителей и потомков, не меняется, т.к. в результате размножения особей путем сигнамии и мейоза частоты аллелей остаются постоянными, а меняются только частоты генотипов. Источником генетической изменчивости особей являются мутации – изменение качественных признаков особей в результате появления новых аллельных форм в отдельных генах или целиком в хромосоме. Тем самым в каждом поколении мутации поставляют в хромосомный набор популяции множество различных генетических вариаций, присущих особям, которых в дальнейшем будем называть мутантами mkt, k≤1.
Процесс изменения содержания генов в хромосоме особей путем мутаций называется мутагенезом. По сути дела, этот фактор эволюции популяции является источником новой генетической информации, не содержащейся ранее в генах генотипов родителей и их потомков.
Мутации являются случайными в том смысле, что не зависят ни от генетического кода особи, содержащейся в ее генотипе, ни от количественных значений фенотипа и степени приспособленности особи. Они происходят спонтанно с определенными вероятностями, заменяя в одном или нескольких локусах тех или иных генов аллельные формы последних новыми значениями аллелей, которые принадлежат генофонду и отличаются от аллелей всех родительских генотипов в том же самом локусе (гене).
Мутации происходят независимо от того, приносят ли они особи вред или пользу. Они не направлены на повышение или понижение степени приспособленности особи, а только производят структурные изменения в аллельных формах генов, меняя тем самым частоту аллелей по отдельным локусам в хромосомном наборе текущего поколения, что, в свою очередь, приводит к изменению количественных признаков особи. В принципе, комбинация мутаций может привести к возникновению новых форм аллелей в некоторых генах генотипа мутанта, которые обеспечивают увеличение его степени приспособленности к внешней среде.
Эволюция популяции в течение смены нескольких поколений в смысле изменения генетической наследственности представляет процесс одновременного и постепенного изменения, как частот, так и форм аллелей в различных локусах хромосомы. При этом аллели действуют на количественные признаки не изолированно друг от друга. Так, влияние того или иного аллеля на степень приспособленности особи зависит от присутствия или отсутствия в его генотипе других аллелей. Набор аллелей каждого локуса взаимно приспособлен (коадаптирован) с набором аллелей других локусов. Поэтому изменение частот аллелей в одном локусе влечет за собой изменение частот аллелей и в других локусах.
Наиболее простым видом мутаций является точечная мутация, связанная с изменением аллеля родительского гена в одном из q бит генной информации (0 заменяется на 1 или 1 заменяется на 0).
Определим интенсивность процесса мутагенеза в t-м поколении как среднее число точечных мутаций Mt(t), которые могут произойти в хромосомном наборе t-й популяции Pt:
Mt(t)=v*(n*q)*Pm,
где v – численность популяции Pt; n*q - длина хромосомы, равная числу битов в бинарной строке E(akt); Pm – вероятность точечной мутации, определяемая как число возможных однобитовых изменений на 100 бит генетической информации. Обычно вероятность мутации очень мала Pm=0,01 или Pm=0,001. Здесь используется n*q потому что обычно длина различных генов совпадает, но в том случае, если гены различной длины, более правильным будет заменить запись n*q на запись q1+…+qn.
Вообще выбор конкретного оператора мутации зависит от конкретной задачи, например в задаче коммивояжера точечная мутация недопустима, поэтому реализуется простая перестановка между двумя битами бинарной строки хромосомы.
4.2.6. Естественный отбор. Третьим фактором эволюции является естественный отбор – процесс, способствующий повышению степени приспособленности особей и предотвращающий разрушительные последствия, которые могут возникнуть в результате мутаций.
Этот процесс можно рассматривать с двух позиций.