Исследование функций и построение графиков
Определение 1. Функция 
называется возрастающей (убывающей) в области X, если для любых двух значений 
верно
(
).
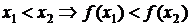Если же верно
(
),
то функция называется неубывающей (невозрастающей). Возрастающая, убывающая, невозрастающая и неубывающая функции называют монотонными функциями.
При изучении поведения функции одним из наиболее важных моментов является нахождение промежутков, в которых функция монотонно возрастает (убывает). Применим к их нахождению понятие производной функции.
Теорема 1. 1) Если функция 
, имеющая производную на отрезке 
, возрастает (убывает) на этом отрезке, то 
(
) для всех 
.
2) Если функция непрерывна на отрезке и дифференцируема на интервале 
, причем 
(
) для всех 
, то эта функция возрастает (убывает) на отрезке .
Аналогично доказывается убывание функции.
Приведенная теорема отражает следующий геометрический факт: у возрастающей функции касательные к ее графику образуют с положительным направлением оси OX острый угол (или, в отдельных случаях, угол, равный нулю), поэтому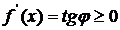 
; для убывающей функции углы наклона касательных --- тупые, поэтому 
.
Пример 1. Исследовать функцию 
на возрастание и убывание. Найдем производную: 
и приравняем ее к нулю 
, откуда находим 
. Таким образом, числовая ось разбивается на два интервала: 
. Найдем знак производной 
на каждом из полученных интервалов, подставив в выражение для производной первого порядка произвольное значение из каждого интервала. Получим 
при 
, следовательно, на 
функция убывает, 
при 
, следовательно, на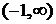 
функция возрастает.
Определение 2. Точка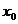 
есть точка максимума (минимума) функции 
, если эта точка лежит внутри такого участка 
, что для всех 
из этого участка, отличных от 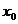, будет 
(
).
Точки 
минимума и максимума функции называются точками экстремума
В определении точки экстремума существенно, чтобы функция была определена как левее, так и правее этой точки, т.е., чтобы эта точка была внутренней, а не граничной точкой промежутка задания функции.
Точки экстремума. Необходимое условие экстремума.
Определение 3. Функцию , заданную на каком-либо промежутке 
, назовем гладкой, если она сама непрерывна на этом промежутке и имеет во всех его точках непрерывную производную.
По отношению к гладким функциям справедлива следующая важная теорема, открытая французским математиком 17-го века П. Ферма.
Теорема Ферма. Если гладкая функция в точке 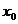имеет экстремум, то ее производная в этой точке обращается в ноль 
=0.
.
Пример 2. Рассмотрим функцию y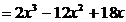 
.
Спрашивается, есть ли у нее точки экстремума и если да, то как их найти. Согласно теореме Ферма, точками экстремума могут быть лишь те точки, в которых производная 
обращается в ноль, (т. е. стационарные точки). Поэтому находим производную и приравниваем ее к нулю 
, откуда 
Теперь нужно выяснить характер поведения функции в этих двух точках. Для этого заметим, что точки 
разбивают всю числовую ось на участки 
, 
Это участки возрастания и убывания функции. Чтобы выяснить, как ведет себя функция на участке 
возьмем произвольную точку, принадлежащую этому интервалу, например, точку 
и подставим ее в производную 
находим 
Значит на интервале функция возрастает. Аналогично, взяв, например, 
найдем